Двойной интеграл в декартовых
координатах ~Свойства двойного
интеграла ~ Вычисление двойного
интеграла ~ Тройной интеграл и его
свойства ~ Вычисление тройного
интеграла в декартовых координатах
Двойной интеграл в декартовых
координатах. Пусть 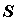 ограниченная
замкнутая область плоскости ограниченная
замкнутая область плоскости 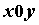 с кусочно-гладкой
границей и пусть функция с кусочно-гладкой
границей и пусть функция 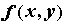 определена и
ограничена на определена и
ограничена на 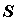 . Посредством сетки кусочно-гладких
кривых разобьем . Посредством сетки кусочно-гладких
кривых разобьем 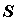 на конечное число элементарных
областей на конечное число элементарных
областей 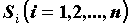 с площадями с площадями 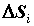 (разбиение (разбиение 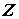 ). Пусть ). Пусть 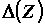 -
наибольший из диаметров областей -
наибольший из диаметров областей 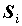 , получающийся при
разбиении , получающийся при
разбиении 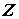 . В каждой из элементарных областей
выберем произвольную точку . В каждой из элементарных областей
выберем произвольную точку 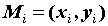 . Число . Число 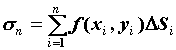 называется интегральной суммой и ставится в
соответствие каждому разбиению
называется интегральной суммой и ставится в
соответствие каждому разбиению 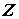 и каждому выбору
точек и каждому выбору
точек 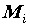 .
Если существует .
Если существует  и он не зависит от
выбора разбиения и он не зависит от
выбора разбиения 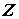 и точек и точек 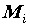 , то функция называется
интегрируемой по Риману в области , то функция называется
интегрируемой по Риману в области 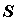 , а сам предел
называется двойным интегралом от функции , а сам предел
называется двойным интегралом от функции 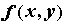 по области по области
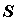 и
обозначается и
обозначается 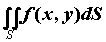 или или 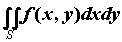 . Двойной интеграл
существует, если . Двойной интеграл
существует, если 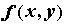 непрерывна на непрерывна на 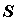 . Допустимы точки
разрыва первого рода, лежащие на конечном числе
гладких кривых в . Допустимы точки
разрыва первого рода, лежащие на конечном числе
гладких кривых в 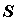 . .
Свойства двойного интеграла. Свойства
двойного интеграла аналогичны свойствам
определенного интеграла:
Линейность:
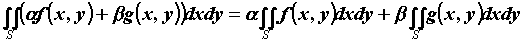 .
Аддитивность: .
Аддитивность:
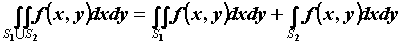 , если
S1 и S2 две области без общих внутренних точек. , если
S1 и S2 две области без общих внутренних точек.
Если для каждой точки 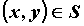 выполнено
неравенство выполнено
неравенство 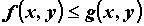 , то , то 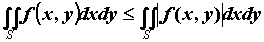 . .
Если 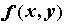 интегрируема на интегрируема на 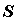 , то функция , то функция 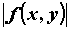 также интегрируема, причем
также интегрируема, причем 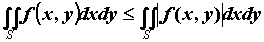 . .
Если 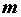 и и 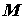 наименьшее и наибольшее значения
функции наименьшее и наибольшее значения
функции 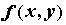 в области, а ее в области, а ее 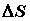 площадь, то площадь, то 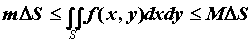 . .
Теорема о среднем значении: если 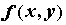 непрерывна
в связной области непрерывна
в связной области 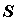 , то существует, по крайней мере,
одна точка , то существует, по крайней мере,
одна точка 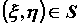 такая, что такая, что 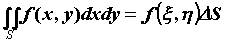 . .
Вычисление двойного интеграла.
Если 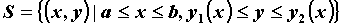 , где - , где - 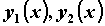 непрерывные на непрерывные на 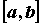 функции, то двойной
интеграл может быть вычислен двумя
последовательными интегрированиями: функции, то двойной
интеграл может быть вычислен двумя
последовательными интегрированиями: 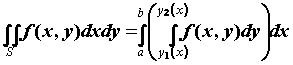 .
Аналогично, если .
Аналогично, если 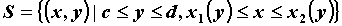 , то , то 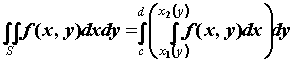 . .
ПРИМЕР 1. Вычисление
двойного интеграла по прямоугольной области.
ПРИМЕР 2. Вычисление двойного интеграла по
области, ограниченной сверху и снизу гладкими
кривыми.
ПРИМЕР 3. Вычисление двойного интеграла по
произвольной области.

Тройной интеграл и его свойства. Пусть 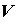 -
ограниченная замкнутая пространственная
область, границей которой является
кусочно-гладкая поверхность, и пусть функция -
ограниченная замкнутая пространственная
область, границей которой является
кусочно-гладкая поверхность, и пусть функция 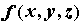 определена
и ограничена в определена
и ограничена в 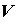 . Посредством сетки кусочно-гладких
поверхностей разобьем . Посредством сетки кусочно-гладких
поверхностей разобьем 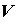 на конечное число
элементарных областей на конечное число
элементарных областей 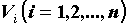 с объемами с объемами 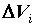 (разбиение
(разбиение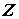 ). Пусть ). Пусть 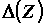 . наибольший из диаметров
областей . наибольший из диаметров
областей 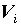 , получающийся при разбиении , получающийся при разбиении 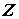 . В каждой
из элементарных областей выберем произвольную
точку . В каждой
из элементарных областей выберем произвольную
точку 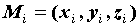 .
Число .
Число 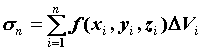 ставится
в соответствие каждому разбиению ставится
в соответствие каждому разбиению 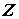 и каждому выбору
точек и каждому выбору
точек 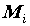 и
называется интегральной суммой. Если существует и
называется интегральной суммой. Если существует
 и
он не зависит от выбора разбиения и
он не зависит от выбора разбиения 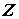 и точек, и точек, 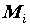 то функция
называется интегрируемой по Риману в области то функция
называется интегрируемой по Риману в области 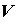 , а сам
предел называется тройным интегралом от
функции , а сам
предел называется тройным интегралом от
функции 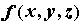 по области по области 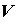 и обозначается и обозначается 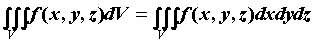 .
Свойства тройных интегралов такие же, как и у
двойных интегралов. .
Свойства тройных интегралов такие же, как и у
двойных интегралов.

Вычисление тройного интеграла в
декартовых координатах. Пусть 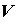 является
цилиндрическим телом, проекция которого на
плоскость является
цилиндрическим телом, проекция которого на
плоскость 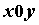 есть область есть область 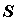 и которое
ограничено снизу поверхностью и которое
ограничено снизу поверхностью 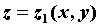 , а сверху v
поверхностью , а сверху v
поверхностью 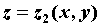 , где , где 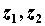 - непрерывные
функции в . Тогда - непрерывные
функции в . Тогда 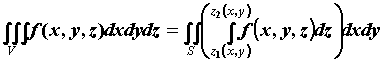 , то есть интегрированием по z
тройной интеграл сводится к двойному интегралу
по области , то есть интегрированием по z
тройной интеграл сводится к двойному интегралу
по области 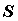 . Для областей более сложной формы
вычисление двойных и тройных интегралов
производится разбиением областей на конечное
число простых областей с уже рассмотренными
свойствами. . Для областей более сложной формы
вычисление двойных и тройных интегралов
производится разбиением областей на конечное
число простых областей с уже рассмотренными
свойствами.
ПРИМЕР 4. Вычисление
тройного интеграла по прямоугольному
параллелепипеду.
ПРИМЕР 5. Вычисление
тройного интеграла по произвольной области.

|

