Локальные экстремумы ~ Исследование на экстремум функции двух
переменных
Локальные экстремумы. Точка 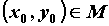 называется точкой локального минимума
(максимума) функции
называется точкой локального минимума
(максимума) функции 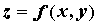 , определенной в области , определенной в области 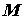 , если
существует окрестность этой точки, такая, что , если
существует окрестность этой точки, такая, что 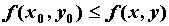 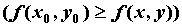 для
всех точек этой окрестности, отличных от для
всех точек этой окрестности, отличных от 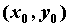 . Такие
экстремумы (максимумы и минимумы) называются
нестрогими. Строгие экстремумы имеют место в
случае, когда выполнены строгие неравенства. . Такие
экстремумы (максимумы и минимумы) называются
нестрогими. Строгие экстремумы имеют место в
случае, когда выполнены строгие неравенства.
ПРИМЕР 1. Исследование на
экстремум по определению.
Исследование на экстремум функции двух
переменных. Обозначим через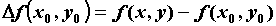 приращение
функции приращение
функции 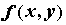 в точке в точке 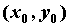 . Если . Если 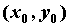 - точка
локального минимума функции - точка
локального минимума функции 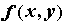 , то существует
окрестность , то существует
окрестность 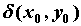 , в которой , в которой 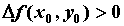 (обратное
неравенство в случае максимума). Из формулы
Тейлора первого порядка (обратное
неравенство в случае максимума). Из формулы
Тейлора первого порядка 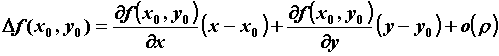 следует, что
приращение следует, что
приращение 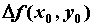 дважды непрерывно
дифференцируемой функции дважды непрерывно
дифференцируемой функции 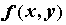 может сохранять
знак, если главная линейная часть приращения
функции в точке экстремума (максимума или
минимума) равна нулю, т.е. выполнено необходимое
условие экстремума: если точка может сохранять
знак, если главная линейная часть приращения
функции в точке экстремума (максимума или
минимума) равна нулю, т.е. выполнено необходимое
условие экстремума: если точка 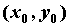 - точка
экстремума, то - точка
экстремума, то 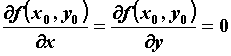 . Такая точка
называется стационарной точкой функции.
Приращение функции в стационарной точке имеет
вид . Такая точка
называется стационарной точкой функции.
Приращение функции в стационарной точке имеет
вид 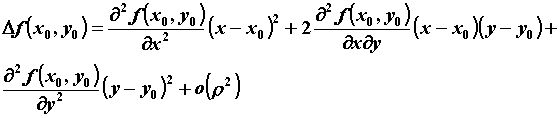 .
Обозначим .
Обозначим 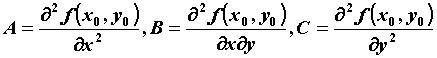 . Справедливо следующее
достаточное условие экстремума. Пусть функция . Справедливо следующее
достаточное условие экстремума. Пусть функция
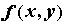 дважды непрерывно дифференцируема в окрестности
точки
дважды непрерывно дифференцируема в окрестности
точки 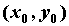 и и 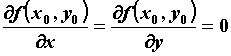 . Если . Если 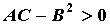 , то в точке , то в точке 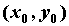 функция достигает экстремума. Если при этом
функция достигает экстремума. Если при этом 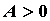 , то этот
экстремум v минимум, при , то этот
экстремум v минимум, при 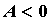 - максимум. Если же - максимум. Если же
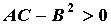 ,
то в точке ,
то в точке 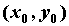 экстремума нет. Геометрически
достаточное условие означает, что в окрестности
экстремума график функции экстремума нет. Геометрически
достаточное условие означает, что в окрестности
экстремума график функции 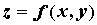 близок к
поверхности близок к
поверхности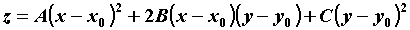 . Если . Если 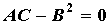 , то для
определения знака приращения , то для
определения знака приращения 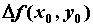 необходимо
изучить члены формулы Тейлора более высокого
порядка. необходимо
изучить члены формулы Тейлора более высокого
порядка.
ПРИМЕР 2. Исследование на
экстремум функции двух переменных.

|

