Формулы Тейлора и Маклорена
~ Аппроксимация функции многочленом
Формулы Тейлора и Маклорена. Если
функция 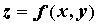 имеет в некоторой окрестности
точки имеет в некоторой окрестности
точки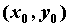 непрерывные частные производные до (n+1)-го
порядка включительно, то для любой точки
непрерывные частные производные до (n+1)-го
порядка включительно, то для любой точки 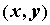 из этой
окрестности справедлива формула Тейлора n-го
порядка: из этой
окрестности справедлива формула Тейлора n-го
порядка: 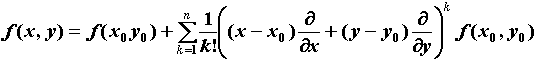 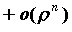 , где , где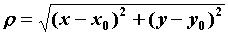 , ,
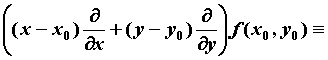
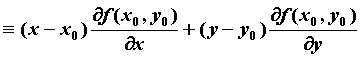 , ,
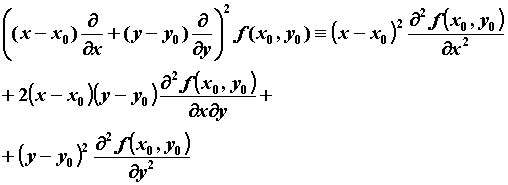
и т.д. Формула Тейлора, записанная в окрестности
точки (0,0) называется формулой Маклорена.
Например, для функции двух переменных при n=2: 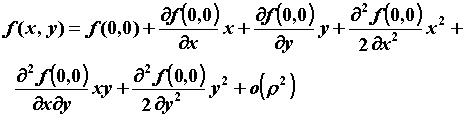 . .
ПРИМЕР 1. Разложение функции
по формуле Тейора в окрестности произвольной
точки.

Аппроксимация функции многочленом.
Выражение
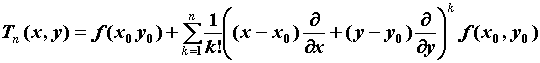 называется многочленом Тейлора n-го порядка.
Поскольку
называется многочленом Тейлора n-го порядка.
Поскольку 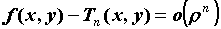 , то в окрестности точки функцию , то в окрестности точки функцию 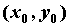 можно
приближенно заменить, или, как говорят,
аппроксимировать, ее многочленом Тейлора, т.е. можно
приближенно заменить, или, как говорят,
аппроксимировать, ее многочленом Тейлора, т.е. 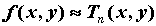 . Чем
ближе точка . Чем
ближе точка 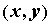 к точке к точке 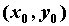 , тем выше
точность такой аппроксимации; кроме того,
точность возрастает с ростом n. Это означает, что,
чем больше непрерывных производных имеет
функция , тем выше
точность такой аппроксимации; кроме того,
точность возрастает с ростом n. Это означает, что,
чем больше непрерывных производных имеет
функция 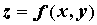 , тем точнее представляет ее
многочлен Тейлора. , тем точнее представляет ее
многочлен Тейлора.
ПРИМЕР 2. Сравнение точности
аппроксимации функции многочленм Тейлора
разного порядка.

|

