Неявная функция одной
переменной ~Неявная функция многих
переменных ~ Производная неявной
функции
Неявная функция одной переменной. Пусть
в некоторой области 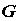 плоскости плоскости 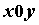 задана
функция задана
функция 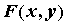 , и пусть линия уровня этой функции
, определяемая уравнением , и пусть линия уровня этой функции
, определяемая уравнением 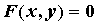 , является
графиком некоторой функции , является
графиком некоторой функции 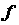 , определяемой
уравнением , определяемой
уравнением 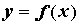 . В этом случае говорят, что
функция . В этом случае говорят, что
функция 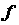 задана неявно уравнением задана неявно уравнением 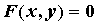 . Для
существования неявной функции требуется
выполнение следующих условий: функция . Для
существования неявной функции требуется
выполнение следующих условий: функция 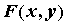 и ее
частная производная по и ее
частная производная по 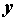 непрерывны в непрерывны в
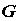 , ,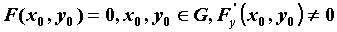 . Тогда в некоторой окрестности
точки . Тогда в некоторой окрестности
точки 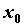 существует единственная
непрерывная функция существует единственная
непрерывная функция 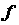 , задаваемая
уравнением , задаваемая
уравнением 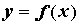 , так, что в этой окрестности , так, что в этой окрестности 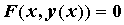 . .
ПРИМЕР 1. Построение
графиков неявных функций одной переменной.
Неявная функция многих переменных.
Аналогично рассматривают функции многих
переменных, заданные неявно. Например, при
выполнении соответствующих условий, уравнение
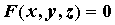 задает неявно функцию задает неявно функцию 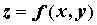 . Это же
уравнение может задавать неявно функцию . Это же
уравнение может задавать неявно функцию 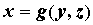 или или
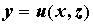 . .
Производная неявной функции. При
вычислении производной неявной функции
воспользуемся правилом дифференцирования
сложной функции. Продифференцируем уравнение 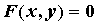 : :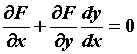 .
Отсюда получим формулу для производной функции .
Отсюда получим формулу для производной функции
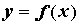 ,
заданной неявно: ,
заданной неявно: 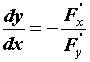 . Таким же
способом нетрудно получить формулы для частных
производных функции нескольких переменных,
заданной неявно, например, уравнением . Таким же
способом нетрудно получить формулы для частных
производных функции нескольких переменных,
заданной неявно, например, уравнением 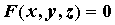 : : 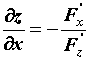 , , 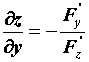 . .
ПРИМЕР 2. Вычисление
производных функций, заданных неявно.

|

