Частные производные ~Производная
по направлению ~ Градиент ~ Полный
дифференциал~ Производные и
дифференциалы высших порядков
Частные производные. Пусть 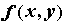 -
функция двух переменных, определенная в
некоторой окрестности точки -
функция двух переменных, определенная в
некоторой окрестности точки 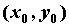 . Если существует
конечный предел . Если существует
конечный предел 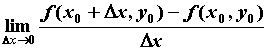 , то говорят, что
функция , то говорят, что
функция 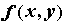 имеет в точке имеет в точке 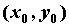 частную
производную по переменной частную
производную по переменной 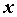 . Аналогично
определяется частная производная по . Аналогично
определяется частная производная по 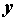 .
Обозначают: .
Обозначают:
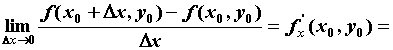
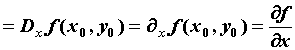 . .
Пусть 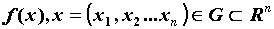 - функция n переменных,
определенная в области - функция n переменных,
определенная в области 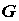 n-мерного
пространства. Частной производной функции n-мерного
пространства. Частной производной функции 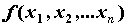 по
переменной по
переменной 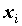 называется предел называется предел
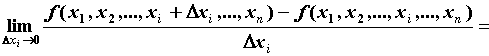
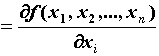 . .
Из определения частной производной следует
правило: при вычислении производной по одной из
переменных все остальные переменные считаем
постоянными, учитывая, что производная
постоянной равна нулю и постоянную можно
выносить за знак производной.
ПРИМЕР 1. Вычисление частных производных.
Производная по направлению. Если в
n-мерном пространстве задан единичный вектор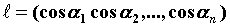 , то
изменение дифференцируемой функции в
направлении этого вектора характеризуется
производной по направлению: , то
изменение дифференцируемой функции в
направлении этого вектора характеризуется
производной по направлению: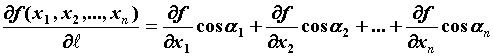 . В частности, для
функции трех переменных . В частности, для
функции трех переменных 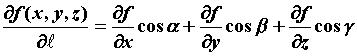 , , 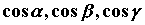 - направляющие
косинусы вектора - направляющие
косинусы вектора 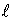 . .
ПРИМЕР 2. Вычисление производных по
направлению.

Градиент. Производная по направлению
представляет собой скалярное произведение
вектора 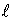 и вектора с координатами и вектора с координатами 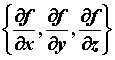 ,
который называется градиентом функции ,
который называется градиентом функции 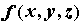 и
обозначается и
обозначается 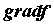 . Поскольку . Поскольку 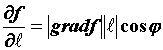 ,
где ,
где 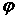 - угол между - угол между 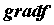 и и 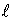 , то вектор , то вектор указывает направление скорейшего возрастания
функции
указывает направление скорейшего возрастания
функции 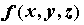 , а его модуль равен производной по
этому направлению. , а его модуль равен производной по
этому направлению.
ПРИМЕР 3. Вычисление градиента функции.

Полный дифференцал. Для приращения
дифференцируемой функции 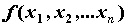 справедливо
равенство справедливо
равенство 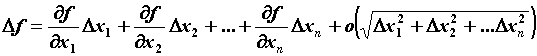 . Линейная по приращениям
аргументов часть приращения функции называется
полным дифференциалом функции . Линейная по приращениям
аргументов часть приращения функции называется
полным дифференциалом функции 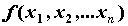 и
обозначается и
обозначается 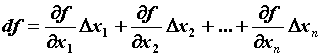 . .
ПРИМЕР 4. Вычисление полного
дифференциала.

Производные и дифференциалы высших
порядков. Дифференцируя частную производную
как функцию нескольких переменных по одной из
переменных, получим производные второго порядка.
Например, для функции двух переменных: 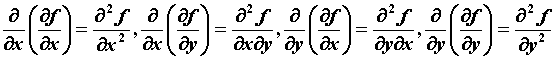 . Если
смешанные производные . Если
смешанные производные 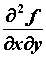 и и 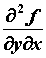 непрерывны, то они равны, то есть не зависят от
порядка дифференцирования. Аналогично
определяются, например,
непрерывны, то они равны, то есть не зависят от
порядка дифференцирования. Аналогично
определяются, например, 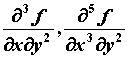 . Если при
вычислении полного дифференциала от
дифференциала первого порядка учесть, что
приращения аргументов . Если при
вычислении полного дифференциала от
дифференциала первого порядка учесть, что
приращения аргументов 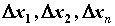 есть числа и
оставить их неизменными, то получим дифференциал
второго порядка. Например, для функции двух
переменных: есть числа и
оставить их неизменными, то получим дифференциал
второго порядка. Например, для функции двух
переменных: 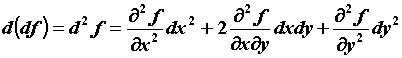 . Здесь учтено равенство смешанных
производных второго порядка и принято . Здесь учтено равенство смешанных
производных второго порядка и принято 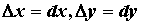 . При
этих допущениях формулу дифференциала любого
порядка можно получить из символического
выражения: . При
этих допущениях формулу дифференциала любого
порядка можно получить из символического
выражения: 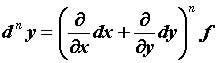 . .
ПРИМЕР 5. Вычисление
производных высших порядков.

|

