Сходимость ряда Фурье,
явление Гиббса ~Приближение функций,
минимальное свойство коэффициентов Фурье ~ Зависимость скорости сходимости от
гладкости функций
Сходимость ряда Фурье, явление Гиббса.
Если функция 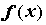 кусочно-гладкая на отрезке кусочно-гладкая на отрезке 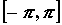 , то ее
тригонометрический ряд Фурье сходится в каждой
точке этого отрезка. При этом, если , то ее
тригонометрический ряд Фурье сходится в каждой
точке этого отрезка. При этом, если 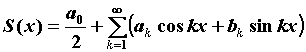 - сумма ряда
Фурье, то для любого - сумма ряда
Фурье, то для любого 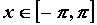 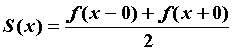 . То есть, если . То есть, если 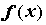 непрерывна
в точке непрерывна
в точке 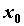 , то , то 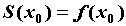 . Если в точке . Если в точке 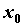 у у
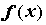 разрыв первого рода, то ряд Фурье
сходится к среднеарифметическому левого и
правого пределов функции в точке разрыв первого рода, то ряд Фурье
сходится к среднеарифметическому левого и
правого пределов функции в точке 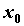 . В окрестности
точек непрерывности функции . В окрестности
точек непрерывности функции 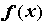 разность между
значением функции в точке и значением частичной
суммы ряда в этой точке стремится к нулю при разность между
значением функции в точке и значением частичной
суммы ряда в этой точке стремится к нулю при 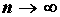 , что
полностью соответствует теории, поскольку в этом
случае , что
полностью соответствует теории, поскольку в этом
случае 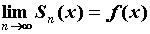 . В окрестности точек разрыва . В окрестности точек разрыва 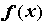 частичные суммы ряда Фурье ведут себя иначе. Эта
особенность поведения частичных сумм Фурье в
окрестности точек разрыва называется явлением
Гиббса. Оно состоит в том, что для некоторых
функций в точке ее скачка
частичные суммы ряда Фурье ведут себя иначе. Эта
особенность поведения частичных сумм Фурье в
окрестности точек разрыва называется явлением
Гиббса. Оно состоит в том, что для некоторых
функций в точке ее скачка 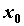 существуют
такие значения существуют
такие значения 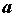 , что , что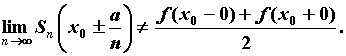
Это не противоречит теории, поскольку у Гиббса
рассмотрен предел 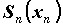 , а в теории v , а в теории v
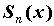 . .
ПРИМЕР 1. Исследование
явления Гиббса.

Приближение функций, минимальное
свойство коэффициентов Фурье. Функция 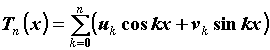 , где , где
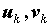 -
произвольные числа, называется
тригонометрическим многочленом.
Тригонометрическим многочленом наилучшего
приближения n-ой степени для функции -
произвольные числа, называется
тригонометрическим многочленом.
Тригонометрическим многочленом наилучшего
приближения n-ой степени для функции 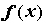 на
отрезке на
отрезке 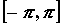 называется такой многочлен называется такой многочлен 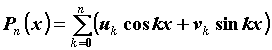 ,
среднеквадратичное отклонение ,
среднеквадратичное отклонение 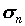 которого от
функции которого от
функции 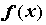 минимально: минимально: 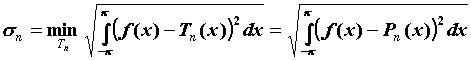 . Для любой
ограниченной интегрируемой на . Для любой
ограниченной интегрируемой на 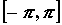 функции
частичная сумма функции
частичная сумма 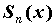 ее ряда Фурье является
тригонометрическим многочленом наилучшего
приближения n-ой степени. ее ряда Фурье является
тригонометрическим многочленом наилучшего
приближения n-ой степени.
ПРИМЕР 2. Нахождение
тригонометрического многочлена наилучшего
приближения.

Зависимость скорости сходимости от
гладкости функций. Скорость сходимости ряда
Фурье функции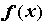 зависит от ее гладкости
(количества непрерывных производных). Если зависит от ее гладкости
(количества непрерывных производных). Если 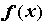 непрерывно дифференцируема r раз на отрезке
непрерывно дифференцируема r раз на отрезке 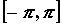 , то
справедливо неравенство , то
справедливо неравенство 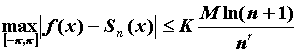 , где , где 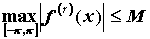 . Для
среднеквадратичного отклонения справедлива
оценка . Для
среднеквадратичного отклонения справедлива
оценка 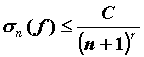 , где , где 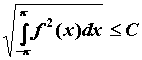 . .
ПРИМЕР 3. Исследование
сходимости ряда Фурье в зависимости от гладкости
функций.

|

