Ряд Фурье, его сходимость ~ Разложение в ряд Фурье на произвольном
отрезке
Ряд Фурье, его сходимость. Пусть
функция 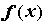 абсолютно интегрируема на отрезке абсолютно интегрируема на отрезке 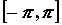 , то есть
существует , то есть
существует 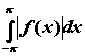 . Тогда ей можно поставить в
соответствие ее тригонометрический ряд Фурье: . Тогда ей можно поставить в
соответствие ее тригонометрический ряд Фурье: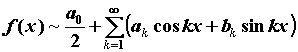 .
Коэффициенты тригонометрического ряда Фурье
называют коэффициентами Фурье и вычисляют по
формулам Эйлера-Фурье: .
Коэффициенты тригонометрического ряда Фурье
называют коэффициентами Фурье и вычисляют по
формулам Эйлера-Фурье: 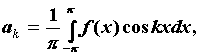 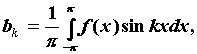 . Если функция . Если функция 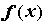 кусочно-гладкая на отрезке
кусочно-гладкая на отрезке 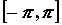 , то ее
тригонометрический ряд Фурье сходится в каждой
точке этого отрезка. При этом, если , то ее
тригонометрический ряд Фурье сходится в каждой
точке этого отрезка. При этом, если 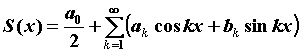 - сумма
ряда Фурье, то для любого - сумма
ряда Фурье, то для любого 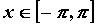 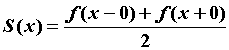 . То
есть, если . То
есть, если 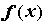 непрерывна в точке непрерывна в точке 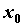 , то , то 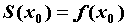 . Если в
точке . Если в
точке 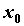 у у 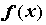 разрыв первого
рода, то ряд Фурье сходится к
среднеарифметическому левого и правого пределов
функции в точке разрыв первого
рода, то ряд Фурье сходится к
среднеарифметическому левого и правого пределов
функции в точке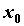 . .
ПРИМЕР 1. Разложение в ряд
Фурье и исследование частичных сумм.
Разложение в ряд Фурье на произвольном
отрезке. Для кусочно-гладкой на отрезке 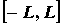 функции функции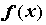 задача
о разложении в ряд Фурье на этом отрезке линейной
заменой сводится к задаче о разложении функции
на отрезке задача
о разложении в ряд Фурье на этом отрезке линейной
заменой сводится к задаче о разложении функции
на отрезке 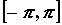 : : 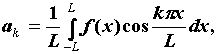 , , 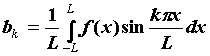 . .
ПРИМЕР 2. Разложение в ряд
Фурье на произвольном отрезке.

|

