Степенные ряды ~ Разложение
функций в ряд Тейлора
Степенные ряды. Функциональный ряд
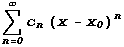 , где , где 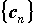 - числовая последовательность,
называется степенным рядом. Степенной ряд
сходится на интервале - числовая последовательность,
называется степенным рядом. Степенной ряд
сходится на интервале 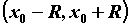 с центром в
точке с центром в
точке 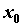 . Число . Число 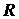 - радиус
сходимости степенного ряда может быть вычислено
по формулам - радиус
сходимости степенного ряда может быть вычислено
по формулам 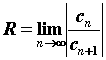 , или , или 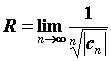 . Степенной ряд
сходится равномерно на любом отрезке, целиком
лежащем внутри интервала сходимости. Сходимость
степенного ряда на границах интервала
сходимости необходимо исследовать специально
для конкретного ряда. . Степенной ряд
сходится равномерно на любом отрезке, целиком
лежащем внутри интервала сходимости. Сходимость
степенного ряда на границах интервала
сходимости необходимо исследовать специально
для конкретного ряда.
ПРИМЕР 1. Нахождение области сходимости
функционального ряда.
Разложение функций в ряд Тейлора. При
исследовании свойств бесконечно
дифференцируемых функций изучают их степенные
ряды ряды Тейлора. Пусть функция 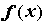 определена в
некоторой окрестности точки определена в
некоторой окрестности точки 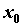 и имеет в этой
точке производные всех порядков. Ряд и имеет в этой
точке производные всех порядков. Ряд
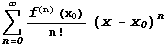 называется
рядом Тейлора для функции называется
рядом Тейлора для функции 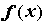 в точке в точке 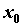 . При . При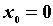 такой
ряд называют также рядом Маклорена: такой
ряд называют также рядом Маклорена: 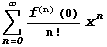 .
Функция .
Функция 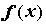 может быть разложена в степенной
ряд на интервале может быть разложена в степенной
ряд на интервале 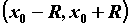 , если существует степенной ряд,
сходящийся к , если существует степенной ряд,
сходящийся к 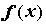 на этом интервале. Если функция
раскладывается в степенной ряд в некоторой
окрестности точки на этом интервале. Если функция
раскладывается в степенной ряд в некоторой
окрестности точки 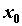 , то это ряд Тейлора. Пусть
функция , то это ряд Тейлора. Пусть
функция 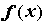 бесконечно дифференцируема на
интервале бесконечно дифференцируема на
интервале 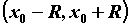 и все ее производные ограничены в
совокупности на этом интервале, то есть
существует число и все ее производные ограничены в
совокупности на этом интервале, то есть
существует число 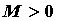 , такое, что для всех , такое, что для всех 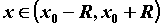 и для
всех и для
всех 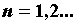 справедливо неравенство справедливо неравенство 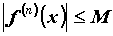 . Тогда
ряд Тейлора сходится к . Тогда
ряд Тейлора сходится к 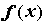 для всех для всех 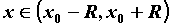 .
Приведем разложения в ряд Тейлора для основных
элементарных функций. .
Приведем разложения в ряд Тейлора для основных
элементарных функций.
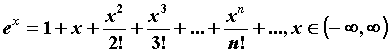
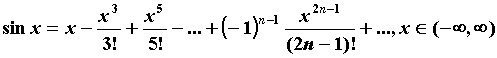
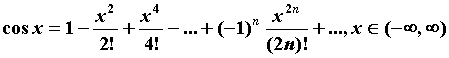
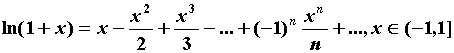
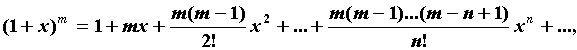
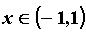
ПРИМЕР 2. Разложение в ряд Маклорена
некоторых элементарных функций.
ПРИМЕР 3. Разложение в ряд
Тейлора с использованием стандартных
разложений.

|

