Функциональный ряд, его
сходимость ~ Равномерная сходимость ~ Исследование на равномерную сходимость
Функциональный ряд, его сходимость.
Рассмотрим ряд, 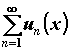 , членами которого являются
функции, определенные на промежутке , членами которого являются
функции, определенные на промежутке 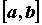 . При
каждом фиксированном . При
каждом фиксированном 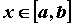 имеем числовой
ряд, сходимость которого может быть исследована
рассмотренными ранее методами. Сумма
функционального ряда имеем числовой
ряд, сходимость которого может быть исследована
рассмотренными ранее методами. Сумма
функционального ряда 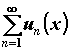 также является
функцией от х: также является
функцией от х: 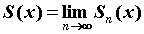 . По определению предела
последовательности: если для . По определению предела
последовательности: если для 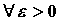 можно указать
номер можно указать
номер 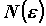 ( что интересно, для каждого
фиксированного ( что интересно, для каждого
фиксированного 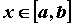 - свой номер, т.е. - свой номер, т.е. 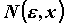 ), такой, что для ), такой, что для
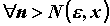 выполняется неравенство выполняется неравенство 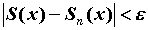 , то это и
означает, что функциональный ряд сходится к
функции , то это и
означает, что функциональный ряд сходится к
функции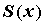 . Множество . Множество 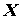 , для которого это
выполняется, называется областью сходимости
функционального ряда. , для которого это
выполняется, называется областью сходимости
функционального ряда.
ПРИМЕР 1. Нахождение области
сходимости функционального ряда.

Равномерная сходимость функционального
ряда. Пусть 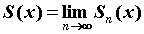 , т.е. функциональный ряд сходится.
Если для , т.е. функциональный ряд сходится.
Если для 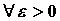 можно указать номер можно указать номер 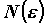 независимо от независимо от 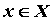 , такой,
что для , такой,
что для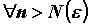 выполняется неравенство выполняется неравенство 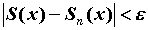 , то
говорят, что функциональный ряд сходится
равномерно на множестве . , то
говорят, что функциональный ряд сходится
равномерно на множестве .
ПРИМЕР 2. Изучение
сходимости функционального ряда.
Исследование на равномерную сходимость.
Признак Вейерштрасса равномерной сходимости
функционального ряда: если существует
сходящийся числовой ряд 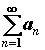 с положительными
членами, такой, что для всех с положительными
членами, такой, что для всех 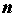 , начиная с
некоторого номера и всех , начиная с
некоторого номера и всех 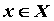 выполняется
неравенство выполняется
неравенство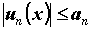 , то функциональный ряд , то функциональный ряд 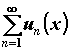 сходится на
сходится на 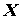 равномерно. Числовой ряд равномерно. Числовой ряд 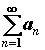 в этом
случае называют мажорантой для функционального
ряда. в этом
случае называют мажорантой для функционального
ряда.
ПРИМЕР 3. Исследование
функционального ряда на равномерную сходимость.

|

