Абсолютная и условная
сходимость ~ Исследование
знакочередующихся рядов
Абсолютная и условная сходимость. Если
в последовательности 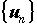 бесконечно много
положительных и отрицательных членов, то ряд
называется знакопеременным. Ряд бесконечно много
положительных и отрицательных членов, то ряд
называется знакопеременным. Ряд 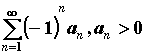 называется
знакочередующимся. Знакопеременный ряд называется
знакочередующимся. Знакопеременный ряд 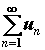 называется абсолютно сходящимся, если сходится
ряд
называется абсолютно сходящимся, если сходится
ряд 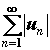 . Если ряд из модулей расходится, а
сам ряд сходится, то его называют условно
сходящимся. Исследование знакопеременного ряда . Если ряд из модулей расходится, а
сам ряд сходится, то его называют условно
сходящимся. Исследование знакопеременного ряда
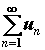 начинают с исследования на сходимость ряда из
модулей
начинают с исследования на сходимость ряда из
модулей 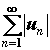 методами для рядов с
неотрицательными членами. Если такой ряд
сходится, то получен ответ: ряд методами для рядов с
неотрицательными членами. Если такой ряд
сходится, то получен ответ: ряд 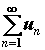 сходится
абсолютно. сходится
абсолютно.
ПРИМЕР 1. Исследование
знакопеременного ряда на абсолютную сходимость.
Исследование знакочередующихся рядов.
Если ряд из модулей расходится, то для
знакочередующегося ряда можно применить признак
Лейбница: если последовательность 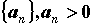 стремится к нулю, монотонно убывая,
стремится к нулю, монотонно убывая, 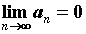 , то ряд , то ряд
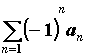 сходится, по крайней мере, условно.
Для знакочередующегося ряда очень просто
оценивается остаток ряда: сходится, по крайней мере, условно.
Для знакочередующегося ряда очень просто
оценивается остаток ряда: 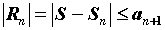 . .
ПРИМЕР 2. Исследование
сходимости знакочередующихся рядов.

|

