Теоремы сравнения ~ Признаки
сходимости
Теоремы сравнения.
1. Рассмотрим два числовых ряда с
неотрицательными членами 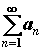 и и 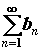 , , 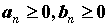 . Если при всех n,
начиная с некоторого номера, . Если при всех n,
начиная с некоторого номера, 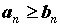 , то из сходимости
ряда , то из сходимости
ряда 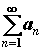 следует сходимость ряда
следует сходимость ряда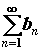 . Наоборот, из
расходимости ряда . Наоборот, из
расходимости ряда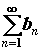 следует расходимость ряда следует расходимость ряда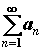 . .
2. Если для таких же двух рядов 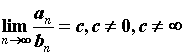 , то оба
ряда или сходятся или расходятся одновременно.
При использовании теорем сравнения нужно иметь
ряд-эталон, с которым сравнивать и про сходимость
которого известно заранее. В качестве таких
рядов чаще всего берут обобщенный гармонический
ряд , то оба
ряда или сходятся или расходятся одновременно.
При использовании теорем сравнения нужно иметь
ряд-эталон, с которым сравнивать и про сходимость
которого известно заранее. В качестве таких
рядов чаще всего берут обобщенный гармонический
ряд 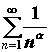 , который сходится при , который сходится при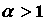 и расходится при и расходится при 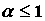 , или
геометрический ряд , или
геометрический ряд 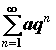 , который сходится при , который сходится при 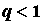 и расходится при и расходится при 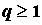 . .
ПРИМЕР 1. Исследование сходимости ряда по
первой теореме сравнения.
ПРИМЕР 2. Исследование сходимости ряда по
второй теореме сравнения.

Признаки сходимости. Признаки
сходимости Даламбера. Для ряда с положительными
членами 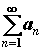 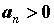 , вычислим , вычислим 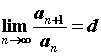 . Если . Если 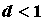 , то ряд сходится, , то ряд сходится, 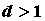 -
расходится. При -
расходится. При 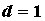 признак Даламбера ответа не дает:
ряд может как сходиться, так и расходиться. признак Даламбера ответа не дает:
ряд может как сходиться, так и расходиться.
Признак сходимости Коши. Для ряда с
неотрицательными членами 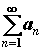 , ,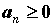 вычислим вычислим 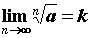 . Если . Если
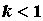 , то
ряд сходится, , то
ряд сходится, 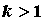 - расходится. При - расходится. При 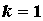 признак Коши
ответа не дает: ряд может как сходиться, так и
расходиться. признак Коши
ответа не дает: ряд может как сходиться, так и
расходиться.
ПРИМЕР 3. Исследование сходимости ряда по
признаку Даламбера.
ПРИМЕР 4. Исследование
сходимости ряда по признаку Коши.

|

