Числовой ряд ~ Сходимость числовго ряда ~ Суммирование числовых рядов
Числовой ряд. Рассмотрим произвольную
числовую последовательность 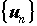 и формально
составим сумму ее членов и формально
составим сумму ее членов 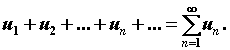 Это выражение
называют числовым рядом, или просто рядом. Члены
последовательности Это выражение
называют числовым рядом, или просто рядом. Члены
последовательности 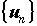 называют членами ряда. Конечно,
невозможно вычислить сумму бесконечного числа
слагаемых, но легко вычислить сумму первых n
членов ряда называют членами ряда. Конечно,
невозможно вычислить сумму бесконечного числа
слагаемых, но легко вычислить сумму первых n
членов ряда 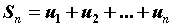 . Эта сумма называется n-ой
частичной суммой. . Эта сумма называется n-ой
частичной суммой.
ПРИМЕР 1. Вычисление
частичной суммы числового ряда.
Сходимость числового ряда. Ряд 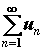 называют сходящимся, если существует и конечен
предел последовательности
называют сходящимся, если существует и конечен
предел последовательности 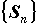 частичных сумм ряда. Сам предел при этом называют
суммой ряда и обозначают
частичных сумм ряда. Сам предел при этом называют
суммой ряда и обозначают 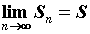 , , 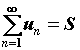 . Если предел
частичных сумм не существует или бесконечен, то ряд
расходится. Разность . Если предел
частичных сумм не существует или бесконечен, то ряд
расходится. Разность 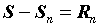 называется
остатком ряда. Очевидно, что для сходящегося
ряда называется
остатком ряда. Очевидно, что для сходящегося
ряда 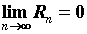 . Это означает, что сумму
сходящегося ряда можно вычислить с любой
точностью, заменяя ее частичной суммой
соответствующего порядка. Для расходящегося
ряда это не так. Поэтому сходимость или
расходимость конкретного ряда является основным
вопросом для исследования. Если ряд сходится,
то . Это означает, что сумму
сходящегося ряда можно вычислить с любой
точностью, заменяя ее частичной суммой
соответствующего порядка. Для расходящегося
ряда это не так. Поэтому сходимость или
расходимость конкретного ряда является основным
вопросом для исследования. Если ряд сходится,
то 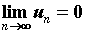 (необходимое условие сходимости
ряда). Обратное, вообще говоря, неверно. Члены
ряда могут стремиться к нулю, но ряд при этом
может расходиться. (необходимое условие сходимости
ряда). Обратное, вообще говоря, неверно. Члены
ряда могут стремиться к нулю, но ряд при этом
может расходиться.
ПРИМЕР 2. Исследование
сходящегося и расходящегося рядов.
Суммирование числовых рядов. Если
возможно найти общий член последовательности
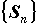 ,
то по определению можно найти и сумму ряда,
вычисляя предел этой последовательности. ,
то по определению можно найти и сумму ряда,
вычисляя предел этой последовательности.
ПРИМЕР 3. Простейшие методы
вычисления суммы ряда.

|

