Математическое
ожидание ~ Дисперсия ~ Моменты
~ Эксцесс ~ Среднее
геометрическое и среднее гармоническое
Каждая случайная величина полностью
определяется своей функцией распределения. В то
же время при решении практических задач
достаточно знать несколько числовых параметров,
которые позволяют представить основные
особенности случайной величины в сжатой форме. К
таким величинам относятся в первую очередь
математическое ожидание и дисперсия.
Математическое ожидание случайной
величины
Математическое ожидание — это число,
вокруг которого сосредоточены значения
случайной величины.
Если x — дискретная случайная величина с
распределением
то ее математическим ожиданием
(обозначается Mx) называется величина,
вычисленная по формуле
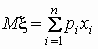 , ,
если число значений случайной величины
конечно, и по формуле
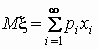 , ,
если число значений случайной величины счетно.
При этом, если ряд в правой части последнего
равенства расходится, то говорят, что случайная
величина x не имеет математического ожидания.
Математическое ожидание непрерывной
случайной величины с плотностью вероятностей px
(x) вычисляется по формуле
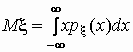 . .
При этом, если интеграл в правой части
равенства расходится, то говорят, что случайная
величина x не имеет математического ожидания.
Если случайная величина h является функцией
случайной величины x, h = f(x ), то
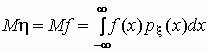 . .
Аналогичные формулы справедливы для функций
дискретной случайной величины:
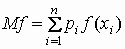 , , 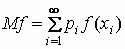 . .
При вычислении математического ожидания
случайной величины полезны следующие его
свойства:
- математическое ожидание константы равно этой
константе, Mc = c;
- математическое ожидание — линейная функция
случайной величины, т.е. при произвольных
постоянных a и bсправедливо: M(ax +bh
) = aMx + bMh;
- математическое ожидание произведения двух независимых
случайных величин равно произведению их
математических ожиданий, т.е. M(xh )=Mx Mh;
Ниже приведены значения математических
ожиданий для наиболее распространенных
распределений:
биномиальное распределение:
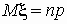 , ,
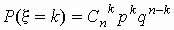 ; ;
геометрическое распределение:
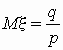 , , 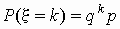 ; ;
гипергеометрическое распределение:
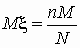 , , 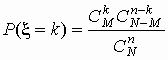 ; ;
пуассоновское распределение:
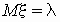 , , 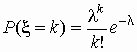 . .
pавномерное распределение:
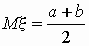 , , 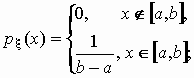
экспоненциальное (показательное)
распределение:
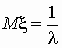 , , 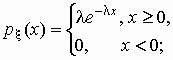
нормальное распределение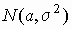 : :
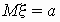 , , 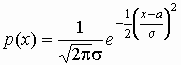 ; ;
распределение хи-квадрат (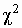 - распределение) с n степенями
свободы: - распределение) с n степенями
свободы:
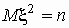 , ,
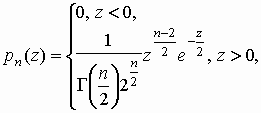
где 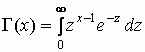 —
гамма-функция Эйлера; —
гамма-функция Эйлера;
распределение Стьюдента с любым числом
степеней свободы:
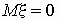 , , 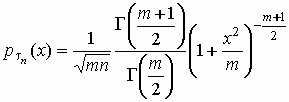 ; ;
F-распределение Фишера с n и m степенями
свободы:
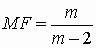 , ,  , ,  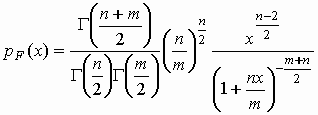 , , 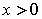 ; ;
распределение Парето имеет математическое
ожидание только при r >1: 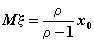 , , 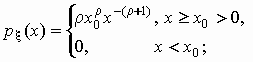
логистическое распределение:
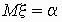 , , 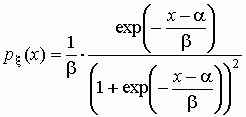 . .
Дисперсия случайной величины
Дисперсия случайной величины характеризует
меру разброса случайной величины около ее
математического ожидания.
Если случайная величина x имеет математическое
ожидание Mx, то дисперсией случайной
величины x называется величина
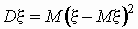 . .
Легко показать, что
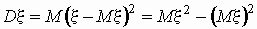 . .
Эта универсальная формула одинаково хорошо
применима как для дискретных случайных величин,
так и для непрерывных. Величина Mx2
вычисляется по формулам 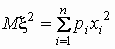 , , 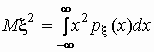
для дискретных и непрерывных случайных величин
соответственно.
Еще одним параметром для определения меры
разброса значений случайной величины является среднеквадратичное
отклонение s x , связанное с дисперсией
соотношением 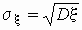 . .
Перечислим основные свойства дисперсии:
- дисперсия любой случайной величины
неотрицательна, Dx >= 0;
- дисперсия константы равна нулю, Dc = 0;
- для произвольной константы D(cx ) = c2Dx
;
- дисперсия суммы двух независимых случайных
величин равна сумме их дисперсий, D(x ± h ) = Dx
± Dh .
Приведем выражения для дисперсий наиболее
распространенных распределений:
биномиальное распределение: 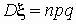 ; ;
геометрическое распределение: 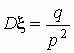 ; ;
гипергеометрическое распределение: 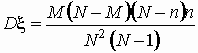 ; ;
пуассоновское распределение: 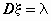 ; ;
pавномерное распределение: 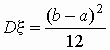 ; ;
экспоненциальное (показательное)
распределение: 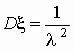 ; ;
нормальное распределение 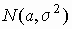 : : 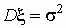 ; ;
распределение хи-квадрат (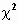 - распределение) с - распределение) с 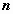 степенями свободы: степенями свободы: 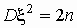 ; ;
распределение Стьюдента с n степенями
свободы, n > 2: 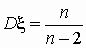 ; ;
F-распределение Фишера с n и m>4 степенями
свободы: 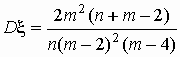 ; ;
распределение Парето имеет дисперсию только
при r > 2: 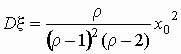 ; ;
логистическое распределение: 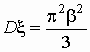 . .
Пример 1. Случайная
величина 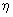 распределена равномерно на промежутке [0, 1].
Найдем математическое ожидание и дисперсию
площади квадрата со стороной
распределена равномерно на промежутке [0, 1].
Найдем математическое ожидание и дисперсию
площади квадрата со стороной 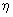 , т.е. характеристики случайной
величины , т.е. характеристики случайной
величины 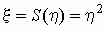 . .
Моменты
В теории вероятностей и математической
статистике, помимо математического ожидания и
дисперсии, используются начальные и
центральные моменты.
Начальным моментом k-го порядка случайной
величины x называется математическое ожидание k-й
степени случайной величины x , т.е. 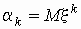 . .
Центральным моментом k-го порядка случайной
величины x называется величина 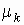 , определяемая формулой , определяемая формулой 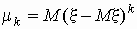 . .
Заметим, что математическое ожидание случайной
величины — начальный момент первого порядка, 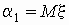 , а дисперсия —
центральный момент второго порядка, , а дисперсия —
центральный момент второго порядка, 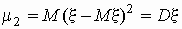 . .
Существуют формулы, позволяющие выразить
центральные моменты случайной величины через ее
начальные моменты. Одна из таких формул
приведена выше: 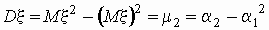 . .
В дальнейшем будет использована формула
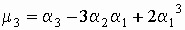 . .
Нетрудно понять, что если плотность
распределения вероятностей случайной величины
симметрична относительно прямой x = Mx , то
все ее центральные моменты нечетного порядка
равны нулю.
В теории вероятностей и в математической
статистике в качестве меры асимметрии
распределения является коэффициент асимметрии,
который определяется формулой
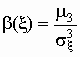 , ,
где 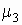 — центральный
момент третьего порядка, — центральный
момент третьего порядка, 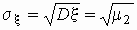 — среднеквадратичное отклонение. — среднеквадратичное отклонение.
Коэффициент асимметрии — безразмерная
величина, а по его знаку можно судить о характере
асимметрии.
Пример 2. Вычислим коэффициент
асимметрии распределения Рэлея, плотность
вероятностей которого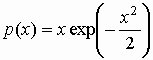 и коэффициент асимметрии распределения с
плотностью вероятностей
и коэффициент асимметрии распределения с
плотностью вероятностей 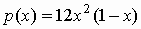 . .
Как видно из проведенных в примере вычислений,
коэффициент асимметрии первого распределения
положителен и у графика плотности вероятностей
"круче левый склон". У второго
распределения, наоборот, коэффициент асимметрии
отрицателен и у графика плотности вероятностей
"круче правый склон".
Эксцесс
Нормальное распределение наиболее часто
используется в теории вероятностей и в
математической статистике и поэтому график
плотности вероятностей нормального
распределения стал своего рода эталоном, с
которым сравнивают другие распределения. Одним
из параметров, определяющих отличие
сравниваемого распределения от нормального,
является эксцесс.
Эксцесс g случайной величины x определяется
равенством 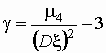 . .
У нормального распределения, естественно, g = 0 .
Если 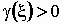 , то это означает,
что график плотности вероятностей , то это означает,
что график плотности вероятностей 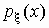 "заострен" сильнее, чем у
нормального распределения, если же "заострен" сильнее, чем у
нормального распределения, если же 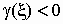 , то
"заостренность" графика , то
"заостренность" графика 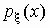 меньше, чем у нормального
распределения. меньше, чем у нормального
распределения.
Пример 3. Вычислим эксцесс для
двух случайных величин, первая имеет
распределение Лапласа (плотность вероятностей 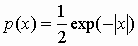 ), а вторая распределена
равномерно на отрезке [-2, 2]. Для сравнения вместе
с графиками плотности вероятностей исследуемых
случайных величин приведем график плотности
вероятностей нормального распределения N(0, 1). ), а вторая распределена
равномерно на отрезке [-2, 2]. Для сравнения вместе
с графиками плотности вероятностей исследуемых
случайных величин приведем график плотности
вероятностей нормального распределения N(0, 1).
Из приведенных в примере 3 вычислений видно, что
график плотности вероятностей распределения с
отрицательным эксцессом имеет боле
“сглаженный” максимум, чем у плотности
вероятностей нормального распределения, а
плотность вероятностей с отрицательным
эксцессом, наоборот, "острее", чем плотность
вероятностей нормального распределения.
Среднее геометрическое и среднее
гармоническое случайных величин, принимающих
только положительные значения
Среднее гармоническое и среднее
геометрическое случайной величины — числовые
характеристики, используемые в экономических
вычислениях.
Средним гармоническим случайной величины,
принимающей положительные значения, называется
величина 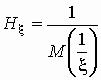 . .
Например, для непрерывной случайной величины,
распределенной равномерно на отрезке [a, b],
0 < a < b среднее гармоническое
вычисляется следующим образом:
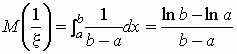 и и 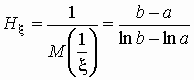 . .
Средним геометрическим случайной величины,
принимающей положительные значения, называется
величина 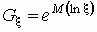 . .
Название "среднее геометрическое"
происходит от выражения среднего
геометрического дискретной случайной величины,
имеющей равномерное распределение
Оно, среднее геометрическое, вычисляется
следующим образом:
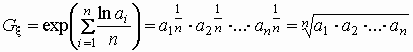 , ,
т.е. получилось традиционное определение
среднего геометрического чисел 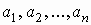 . .
Вычислим среднее геометрическое случайной
величины, имеющей, например, показательное
распределение с параметром l :
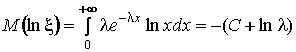 , , 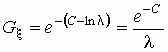 , ,
где 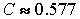 —
постоянная Эйлера, —
постоянная Эйлера,
Пример 4. Случайная величина x
распределена равномерно на отрезке [2, 3]. Найдем
для нее среднее гармоническое и среднее
геометрическое.

|

