Условие
совместности ~ Исследование
неоднородной системы. Частное решение
Рассмотрим неоднородную систему m
линейных алгебраических уравнений относительно n
неизвестных
x1 , x2 , ..., xn:
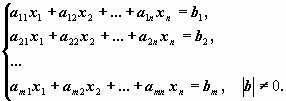
В отличие от однородной системы, эта система
совместна не всегда.
Справедливо следующее утверждение (теорема
Кронекера-Капелли).
Для того, чтобы неоднородная система линейных
алгебраических уравнений была совместна,
необходимо и достаточно, чтобы ранг расширенной
матрицы системы совпадал с рангом матрицы
системы.
ПРИМЕР 1. Проверка условия
совместности неоднородной системы.
Исследовать неоднородную систему
— это значит установить, является ли она
совместной, и если является — найти выражение
для общего решения системы.
Исследуем неоднородную систему методом
Гаусса.
Пусть
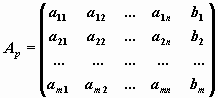
расширенная матрица исследуемой системы, ранг
которой r равен рангу матрицы системы и r<
n.
Такая матрица приводится Гауссовым
исключением к ступенчатому виду
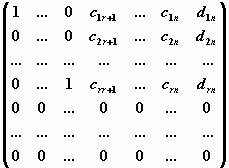 . .
Соответствующая эквивалентная система имеет
вид
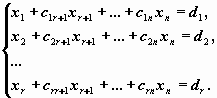
Отсюда легко получить выражения базисных
переменных x1 , x2 , ..., xr
через свободные переменные xr+1 , xr+2 ,
..., xn . Формулы
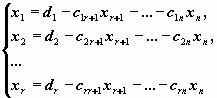
определяют общее решение системы. Положив
свободные переменные равными нулю, xr+1 =0, xr+2
=0, ..., xn=0, и вычислив соответствующие
значения базисных переменных, получим частное
решение исследуемой системы
x1 =d1 , x2 =d2 , ..., xr=dr
, xr+1 =0, xr+2 =0, ..., xn=0.
ПРИМЕР 2. Исследование
неоднородной системы для двух различных правых
частей методом Гаусса.

|

