Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4 ~ Пример 5 ~ Пример 6

Пример 1. Написать каноническое уравнение плоскости, перпендикулярной вектору n={3,1,1} и проходящей через точку М(2,-1,1).

Решение примера в среде пакета Maple

Теоретическая справка

Пример 2. Написать каноническое уравнение плоскости, содержащей точки K(2,1,-2), L(0,0,-1), M(1,8,1).

Решение примера в среде пакета Maple

Теоретическая справка

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Написать канонические и параметрические уравнения прямой, параллельной прямой 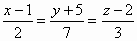, проходящей через точку М(1,2,3).

Решение: Необходимая для решения точка задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для заданной, т.к. они параллельны: n={2,7,3}. Осталось воспользоваться формулой.

Ответ: .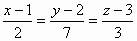

Решение примера в среде пакета Maple

Теоретическая справка

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей

Написать канонические уравнения прямой, заданной пересечением двух плоскостей: 2x – y + 3z + 3 = 0 и 3x + y + z – 6 = 0.

Решение примера в среде пакета Maple

Теоретическая справка

Пример 5. Найти точку пересечения прямой и плоскости

Найти точку А пересечения прямой 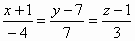и плоскости 2x–y+3z+3 = 0.

Решение примера в среде пакета Maple

Теоретическая справка

Пример 6. Найти расстояние от точки до плоскости

Найти расстояние от точки (1,3,2) до плоскости 3x + y + z – 6 = 0

Решение примера в среде пакета Maple

Теоретическая справка