Описание продукта CurvXML
CurvXML, представляет собой программный продукт для отображения и хранения различных
математических кривых. Реализованный подход позволяет, не заботитясь о способах хранения и вычисления
кривых, сосредоточиться на главных задачах:
- наглядное представление и отображение различных математических кривых;
- удобное управление данными кривых.
Компонентная структура
Для реализации продукта были использованы два внешних компонента:
- CioinaEval
для вычисления значений функций;
- NewLife Document Components Package
для интерпретирования XML - документов.
Вычисление функций
Компонент CioinaEval был выбран из нескольких подобных (интепретирующих строку, как математическое
выражение, и позволяющих определять пользовательские функции и переменные). Он обладает, на наш
взгляд, наименьшим количеством ограничений и наибольшим количеством возможностей:
- позволяет обрабатывать не только выражения, но и целые пользовательские функции,
написанные на квазиязыке;
- количество параметров и длина выражения не ограничены;
- контроль ошибок синтаксиса;
- возможность интеграции с пакетом Mathematica.
Представление и хранение данных
Данные кривых хранятся в формате XML, позволяющем описывать данные произвольного типа.
XML-документы выполняют роль универсального формата обмена информацией.
Не ограничивая автора каким-либо фиксированным набором выражений, XML позволяет ему вводить любые имена,
представляющиеся полезными. Эта возможность является ключевой для активного манипулирования данными
различных прикладных областей.
Благодаря хранению данных в таком формате был реализован унифицированный подход к математическим кривым:
- иерархическое представление данных (головной элемент - XML-документ; его дочерние элементы -
математические кривые, - потомки которых формулы соответствующих кривых);
- возможность простого редактирования и добавления новых данных (кривых).
Особенности подхода
Если кривая представлена прерывающейся линией (конхоида Никомеда, Декартов овал,
лемниската Бернулли, трактриса, овалы Кассини и др.), предлагается строить каждую непрерывную часть отдельно.
Такой подход резко упрощает поставленные задачи.
Дополнительной возможностью программы является «совмещение» кривых: при рисовании очередной
кривой можно воспользоваться рисунком с ранее начерченной, при этом масштаб не пересчитывается.
Примеры
Для демонстрации возможностей программы рассмотрим описание нескольких математических кривых.
Декартов овал
Задание его в параметрических координатах элементарно:
Y=R*sin(t); X= R*cos(t)
Значение параметра R определяется из квадратного уравнения, значения одного из коэффициентов
которого зависят от значения t:
(M^2-1)*R^2 - 2*R*( M^2*d*cos(t) – A ) + (M*d)^2 – A^2 = 0
Для построения такой кривой на встроенном языке описывается функция R(t).
Значения этой функции зависят от значения дискриминанта, который обращается в ноль при параметре
кривой |М|=1. Т.е. при |М|=1 уравнение имеет один корень, в случае |М| не равном 1 и неотрицательном
дискриминанте - два.
R(t)~ if(eq(abs(M),1),
(1/2)*((d^2-A^2)/(d*cos(t)-A)),
(M^2*d*cos(2*pi*t)-A)-sqrt((M^2*d*cos(2*pi*t)-A)^2-(M^2-1)*(M^2*d^2-A^2))/(2*(M^2-1)))
Лемниската БернуллиЗадание ее в параметрических координатах выглядит так же, как и у Декартового овала:
Y=R*sin(t); X= R*cos(t)
Но значение параметра R рассчитываются более простым способом: 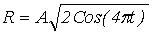
R(t)~ A*sqrt(2*cos(2*t))
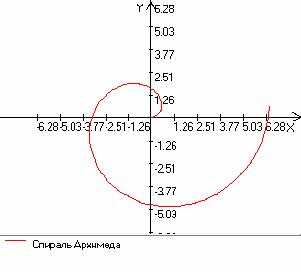
Спираль Архимеда
Параметрическое задание:
x = t * Cos (t); y = t * Sin (t), где t oт 0 дo бесконечности.
Спираль Архимеда получается как траектория точки, движущейся равномерно по прямой,
которая вращается вокруг точки, принадлежащей этой прямой. В момент движения движущаяся точка совпадает
с центром вращения прямой.
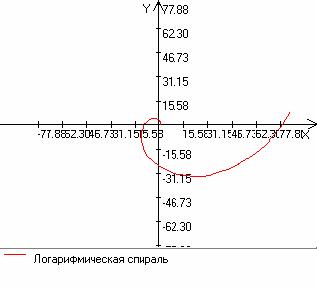
Логарифмическая спираль
Кривую эту можно было бы назвать по имени Декарта, так как впервые о ней говорится в одном из его
писем (1638 г.). Однако подробное изучение ее свойств было проведено только полвека спустя Якобом Бернулли.
На современных ему математиков эти свойства произвели сильное впечатление. На каменной плите,
водруженной на могиле этого знаменитого математика, изображены витки логарифмической спирали.
Архимедову спираль описывает точка, движущаяся вдоль луча так, что расстояние от начала луча
возрастает пропорционально углу его поворота: r = ka. Логарифмическая спираль получится, если потребовать,
чтобы не само расстояние, а его логарифм возрастал прямо пропорционально углу поворота.
Спираль Корню(спираль Эйлера, клофоида)
Процесс построения кривой интересен тем, что границы (Xmin, Ymin, Xmax, Ymax) определяются по формуле
в зависимости от значения параметра.
Параметрическое задание кривой является достаточно сложным:
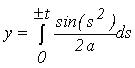 , ,
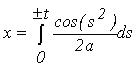 , где t oт 0 дo бесконечности.
Функция, вычисляющая значение интеграла, является внешней и выглядит следующим образом: , где t oт 0 дo бесконечности.
Функция, вычисляющая значение интеграла, является внешней и выглядит следующим образом:
integral_KCos(a, b)~ bk(ex=0.00001, N=4, X0=0, s1=0, s0=0+3*ex,
while (gr(abs(s1-s0), ex), bk(s0=s1, h=(b-a)/N, su=0, i=0,
while(lseq(i, N-1), bk(x0=a+i*h, su=su+h*(cos(x0^2)/(2*c)+cos((x0+h)^2)/(2*c))/2, i=i+1)), s1=su, N=N*2)), s1),
integral_KSin(a, b)~ bk(ex=0.00001, N=4, X0=0, s1=0, s0=0+3*ex,
while (gr(abs(s1-s0), ex), bk(s0=s1, h=(b-a)/N, su=0, i=0,
while(lseq(i, N-1), bk(x0=a+i*h, su=su+h*(sin(x0^2)/(2*c)+sin((x0+h)^2)/(2*c))/2, i=i+1)), s1=su, N=N*2)), s1).
В процессе работы с программой предоставляется возможным:
- изменение границ интегрирования (вплоть до задания их от любой функции);
- изменение способа (либо условностей описанного способа) расчета значения интеграла путем внесения изменений в код описания;
- изменение значений границ;
- изменение параметров;
- изменение начального и конечного значения t;
- изменение шага табулирования.
Стоит отметить интересную особенность начертания кривых в зависимости от шага.
Например, рассмотрим производную гипоциклоиды – кривую Штейнера. Ее красиво можно окрестить «рыбкой»:
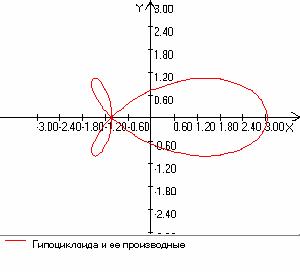
При шаге равном pi/32 изображение значительно отличается от того, что получается при шаге pi/5:
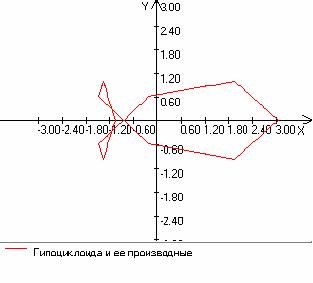
И в заключении хотелось бы сказать следующее. В реализации данного продукта был найден
унифицированный подход к представлению и изменению данных математических кривых. Такой подход обеспечвает возможность:
- изменения значений параметров (например, присвоение им значений функции) и уравнений, определяющих кривую;
- изменения границ построения;
- использования пользовательских переменных и функций.
– в процессе работы программы
Наверх
|

