|
Стереографическая проекция 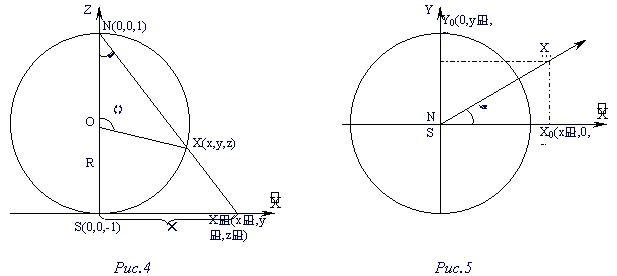
Пусть сфера единичного радиуса с центром в
точке О (0, 0, 0) касается пополненной плоскости z=-1 в
южном полюсе S(0, 0, -1).
Выберем на плоскости произвольно точку Х' с
координатами (х', у', -1). Полученная точка Х
пересечения отрезка Х'N (рис.4) со сферой –
стереографическая проекция точки Х' на сферу.
Обозначим ее координаты через (x, y, z) и найдем их.
Известно, что декартовы координаты точки через
сферические выражаются следующими формулами:
x = R cosa sinq , y = R sina sinq , z = R cosq
.
Введем следующее обозначение: r =
SX'. Тогда по рис. 5
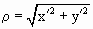 , NX'= , NX'= 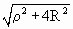 . .
Рассмотрим D NOX. Применяя теорему
синусов, получаем
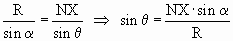 . .
Рассматривая подобные треугольники NSX' и NSX,
получим, что
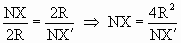 или или 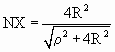 . .
При этом 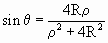 .
Следовательно .
Следовательно 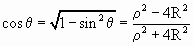 . .
По рис.4: 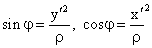 . .
Таким образом, получаем координаты точки Х –
стереографической проекции точки Х':
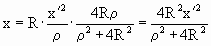 , , 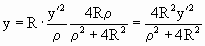 , , 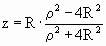 . .
Но в нашем случае радиус сферы равен 1, тогда
формулы приобретут вид:
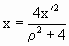 , , 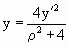 , ,
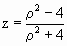 . .
Конформные преобразования
Пусть сфера единичного радиуса с центром в
точке О (0, 0, 0) касается пополненной плоскости z=-1 в
южном полюсе S(0, 0, -1).
Будем рассматривать конформные
дробно-линейные преобразования, которые
переводят окружность с координатами (x, y, -1) в
окружность с координатами (х' , у', -1). Подвергнем
ее конформному преобразованию вида
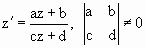 , ,
где a, b, c, d, z – комплексные.
Очевидно комплексная координата z = x+iy. Зная z,
можем получить z', а, следовательно, и координаты
окружности, полученной в результате
преобразования. При этом x'=Re(z), y'=Im(z).
Экваториальная плоскость 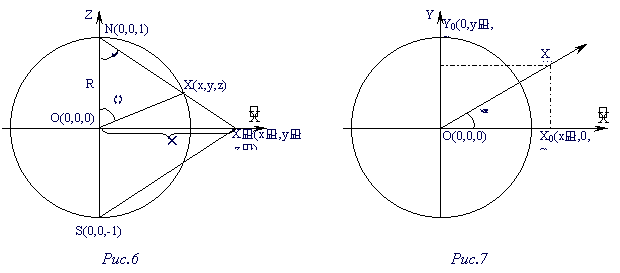
Пусть пополненная ХY-плоскость проходит через
центр О(0,0,0) сферы единичного радиуса, т.е.
является плоскостью экватора.
Выберем на плоскости произвольно точку Х' с
координатами (х', у', 0). Полученная точка Х
пересечения отрезка Х'N (рис.6) со сферой –
стереографическая проекция точки Х' на сферу.
Обозначим ее координаты через (x, y, z) и найдем их.
Снова применим сферические координаты точки,
через которые можем найти ее декартовы
координаты:
x = R cosa sinq , y = R sina sinq , z = R cosq
.
Введем следующее обозначение: r =
ОX'. Тогда
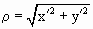 , NX'= , NX'= 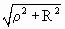 . .
Рассмотрим D NOX. Применяя теорему
синусов, получаем
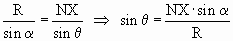 . .
Рассматривая подобные треугольники NОX' и NХS,
получим, что
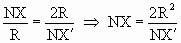 или или 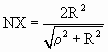 . .
При этом 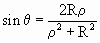 .
Следовательно .
Следовательно 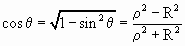 . .
По рис.7: 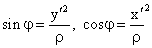 . .
Таким образом, получаем координаты точки Х –
стереографической проекции точки Х':
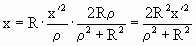 , , 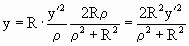 , ,
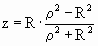 . .
Но в нашем случае радиус сферы равен 1, тогда
формулы приобретут вид:
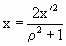 , , 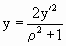 , ,
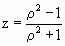 . (1) . (1)
Как сказано выше, дробно-линейное конформное
отображение вида
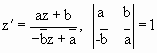
соответствует повороту на сфере SU(2)>SO(3).
Если b=0, то неподвижными точками являются z1=0
и z2=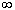 . .
Если b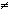 0, то неподвижными будут точки 0, то неподвижными будут точки 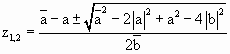 . При чем х=Re(z) и y=Im(z). . При чем х=Re(z) и y=Im(z).
Пусть l, m, n координаты неподвижной точки на
сфере, полученные применением преобразования (1)
к точке (3).
Пусть (х', y', z' ) – координаты стереографической
проекции точки (x, y, 0). Пусть также точка (x1, y1,
0) – отображение точки (x, y, 0) конформным
преобразованием (2), а (х", у", z" ) –
стереографическая проекция точки (x1, y1,
0).
Расстояние между точками (х', y', z' ) и (х", у", z")
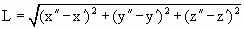 . .
Расстояние от этих точек до прямой, проходящей
через неподвижные точки на сфере (оси вращения) 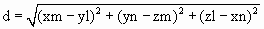 . .
Угол поворота относительно оси вращения,
переводящей (х', y', z' ) в (х", у", z" ) 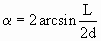 . .
Список литературы
- Бакельман И.Я. Высшая геометрия, М.: Просвещение,
- 1967 г.
- Постников М.М. Аналитическая геометрия, М.: Наука
– 1973 г.
- Ф. Клейн Лекции об экосаэдре и решение уравнений
пятой степени, М: 1989 г.
- Дьяконов А.Г. Matlab 5, М: 2000 г.
|

