1. Описание конформной геометрии в координатах

Запишем уравнение сферы в прямоугольных координатах с началом в центре сферы

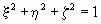.                                                                                   (1)

Введем теперь комплексную величину z=x+iy, изображая вначале x+iy обычным образом на xh - плоскости (плоскость экватора), а затем отображая эту плоскость с помощью стереографической проекции на полюса x=0, h=0, z=1 однозначно на поверхность сферы. Мы получаем формулы

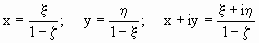                                           (2)

или

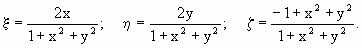.                  (3)

Поскольку мы хотим определить те дробно-линейные подстановки z, которые соответствуют вращениям сферы, для нас представляют интерес диаметрально противоположные точки сферы (так как при каждом вращении одна из пар таких точек остается неподвижной). Чтобы получить искомое соотношение, изменим в (2) знаки x, h и z. Тогда для диаметрально противоположной точки получим

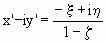
и отсюда, умножая на x+iy и учитывая (1),

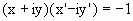,                                                                           (4)

или, записывая x+iy в виде ,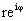

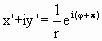.                                                                                   (5)

Диаметрально противоположным точкам отвечают комплексные числа, у которых абсолютные величины обратны друг другу, а аргументы отличаются на p.

Рассмотрим теперь вращение на угол a вокруг оси 0-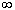 (перпендикулярной к плоскости экватора) против часовой стрелки, если смотреть извне сферы на ее верхний полюс. Пусть точка z переходит при этом в z'. Нас интересует, как z' связана с z. Ясно, что таким же образом, как x' +ih и x +ih при повороте x h -плоскости указанным образом, поскольку знаменатель 1-z в формулах (2) при вращении не меняется. Если направить ось x вправо, а ось h от нас, то справедливы хорошо известные формулы

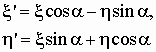
или

,

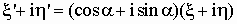откуда следует

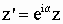                                                                                          (1)

Если мы хотим теперь аналогично записать вращение на угол a вокруг оси, соединяющей (x ,h ,z ) и (-x ,-h ,-z ), где первая точка играет ту роль, что и точка 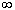выше (т.е. поворот совершается против часовой стрелки, если смотреть извне на точку (x ,h ,z )), то мы должны подставить в (6) вместо z и z' соответственно, которые обращаются в 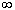в точке (x ,h ,z ) и в 0 в точке (-x ,-h ,-z ). Такая дробно-линейная функция определена однозначно с точностью до множителя; она имеет вид

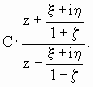
Множитель С нет необходимости определять, поскольку он все равно исчезает из окончательной формулы. В самом деле, подставляя в (6) наше выражение для z, получаем независимо от С

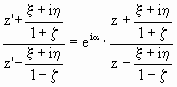
или после небольших преобразований

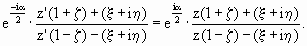                             (2)

Это - общая искомая формула для вращения. Если разрешить ее относительно z' и ввести обозначения

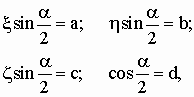                                                          (3)

где, очевидно,

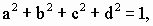                                                                    (4)

то мы получим

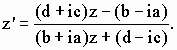                                                              (5)

Мы получили при этом (как можно было бы сообразить заранее) две формулы для каждого вращения сферы. А именно, вращение не изменится, если увеличить угол a на 2p . При этом все четыре величины в формулах (8) изменяли знак. Это согласуется с тем, что определитель преобразования (10) равен 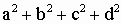. В силу (9) он равен 1, и это составляет для знаков a, b, c, d ровно две возможности.

Одновременно мы получаем удобное правило для вычисления косинуса половины угла поворота, заданного формулой

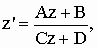
и тем самым для определения периода этого преобразования (если вообще мы имеем дело с периодическим преобразованием). А именно, сравнение (10) дает

В начало

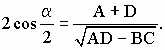
Далее