© Ф.Пинежанинов
В начало
Зеркало: http://pinega.da.ru/
Программирование метода конечных элементов
неотделимо от графического представления
результатов по трем причинам. Первая в том, что в
силу численного характера результаты решений,
это множество цифр ассоциированных с областями
геометрического пространства, и для того, чтобы
не перегружать человека излишними усилиями по
использованию пространственного воображения, а
дать возможность принять разумное решение на
основе видения картины в целом. Вторая, тесно
связанная с первой, связана со стилем
мышления инженеров-конструкторов. Им привычен
стиль мышления присущий скорее художникам, чем
бухгалтерам и графическое представление важнее
для их интуиции, чем скучные колонки цифр, хотя,
иногда и таблички не мешают. Такая уж у них
работа, требующая фантазии художника, точности
бухгалтера и понимания психолога. Но только они и
могут видеть воплощение своих мыслей в металле,
бетоне и других неодушевленных предметах
материального мира. И третья причина связана с
описанием задачи, не просто описать геометрию
сложного объекта, но с силу определенной
регулярности инженерных конструкций обычно их
можно строить из более простых образов с помощью
некоторых регулярных преобразований.
Таким образом будем рассматривать три объекта:
предмет рассмотрения, образ рассмотрения и
наблюдателя, или, вспомнив обычные гегелевские
триады, например "единство и борьба..."
сосредоточимся на "и". В случае машинной
графики роль "и" выполняет экран компьютера.
Нарисуем картинку:
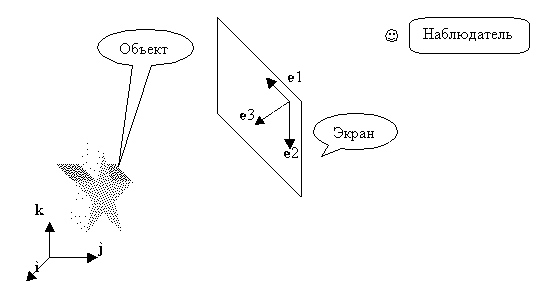
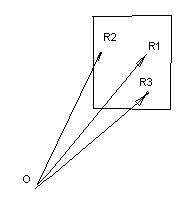
Наблюдатель не может непосредственно
наблюдать объект, хотя бы потому что объекта нет,
а есть его образ в виде набора цифр, которые
описывают его геометрию свойства, деформацию,
напряжения и другие. Объект или модель, как
правило описывается в некоторой системе
координат, связанной с этой моделью. Система
координат связанная с объектом, в машинной
графике обычно называется мировой системой,
чтобы подчеркнуть ее связь с миром, который мы
хотим изображать на экране. Пусть эта система
определена с помощью 3 базисных векторов { i,
j, k }, где i={1,0,0}; j={0,1,0}; k={0,0,1},
понятно, что любая точка обьекта описывается
линейной комбинацией этих векторов x= x i + y
j + z k и это геометрический объект, с
другой стороны на вектор можно смотреть как на
тройку чисел - координат {x,y,z} в смысле
принятом в алгебре. Здесь и далее жирными
буквами будем обозначать векторы, а прописными
координаты, или коэффициенты при векторах или
координаты векторов.
С экраном , удобно связать другую систему
координат, которую обычно называют системой
координат экрана. Пусть в системе координат
экрана, которая определяется тремя векторами { e1,
e2, e3 } мы умеем рисовать , точнее, умеем
изображать точки, которые определяются
координатами в базисе { e1, e2, e3 }.
Другими словами – первые две координаты можно
использовать в качестве параметров в методах
типа MoveTo или LineTo в GDI или их аналогах в других
графических контекстах.
Таким образом, если объект, описанный в мировом
базисе { i, j, k }, удастся
представить в базисе экрана { e1, e2, e3 },
другими словами найти координаты в экранном
базисе, то только тогда сможем и нарисовать его.
Основная задача компьютерной графики может быть
сформулирована так : для объекта, описанного
координатами в мировом базисе, надо найти
координаты в экранном базисе. На картинке
изображены два правых базиза, но в силу
установившихся традиций в системах машинной
графики, с экраном часто связывают левостороннюю
систему координат. Это не очень удобно для
дальнейших рассуждений, так как усложняет
использование векторной алгебры, поэтому будем
считать обе системы правосторонними, а все
необходимые изменения всегда сможем внести за
счет координат векторов базиса { e1, e2, e3
}.
Векторы можно рассматривать в двух видах:
свободных, которые определяются только длиной и
направлением; и определенных, которые
определяются длиной, направлением и точкой
начала. Понятно, что можно задавать и множество
других ограничений на начало вектора и получать
некоторые другие типы векторов. Наиболее общими
свойствами обладают свободные векторы и с их
помощью удобно рассуждать, наиболее удобными для
вычислений свойствами обладают определенные
векторы, потому, что все операции с ними могут
быть описаны с помощью матричных преобразований.
Будем пользоваться и теми и другими, тем более,
что между ними легко установить связь. Подробнее
с вопросами векторного исчисления можно
познакомиться в прекрасной книге Кочина, а о
более абстрактном подходе в замечательной книге
Клейна.
Пусть вектор O связывает начало мировой
системы координат с началом экранной системы
координат, вектор R задает произвольную
точку пространства в виде вектора направленного
из начала мировой системы координат, а r
задает ту же точку пространства в виде вектора,
направленного из начала экранной системы
координат. Таким образом задав вектор, O
связывающий начала двух систем координат, всегда
можем переходить от r к R и обратно с
помощью обычных соотношений векторной алгебры
R=r+O и r=R-O.
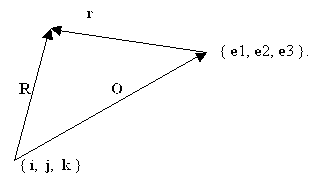
Пусть вектор O и тройка векторов { e1, e2,
e3 } заданы, тогда для любого вектора
пространства существует представление в виде
линейной комбинации векторов базиса экрана r=
r1 e1 + r2 e2+ r3 e3, где {r1, r2, r3} суть
координаты точки в базисе экрана и, как
отмечалось выше, если они известны, то легко
можем рисовать. При этом для рисования на
плоскости достаточно двух первых координат, а по
третьей координате можем судить об удаленности
от экрана.
С учетом предыдущего можем записать R-O= r1 e1 + r2 e2+ r3 e3
и последовательно скалярно умножая это
равенство на базисные векторы экрана можем
записать выражение в матричном виде:
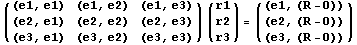
Здесь выражение (*,*) обозначает скалярное
произведение векторов.
Таким образом, если в терминах координат мирового базиса заданы
базисные векторы экрана { e1, e2, e3 } и
вектор смещения начала координат экранного
базиса O, то для любой точки мирового
пространства, описываемой вектором R, решая
систему линейных уравнений, легко найти
координаты {r1, r2, r3} этой точки в экранном
базисе, а следовательно и нарисовать ее. Еше
несложно заметить, что координаты точки в
экранном базисе являются линейными функциями от
координат в мировом базисе, а значит добавив еще
одну абстрактную координату, можно набор
линейных функций превратить в линейное
отображение, что достаточно часто и используется
в системах трехмерной машинной графики,
например в Open GL если Вам нравится язык
программирования C, или Direct3D если предпочитаете C++. Покажем
как это делается.
Сначала общее определение однородных
координат. Объект из n –мерного линейного
пространства, возможно представить как объект в
n+1 линейном пространстве. Во многих случаях, это
полезно, так как сложные соотношения при
рассмотрении их во вспомогательном
пространстве оказываются более простыми и
понятными, и вычисления можно осуществлять по
однообразной схеме, что важно при
программировании. Такое представление не
единственно и их может быть бесконечно много.
Однородные координаты, это один из способов
такого расширения, когда дополнительная
координата S, называемая масштабным фактором,
вводится как n+1 координата, таким образом, чтобы
вектор (X1, X2, ... Xn) в n –мерном пространстве, имел
представление (S X1,S X2, ...S Xn, S) . Таким образом
проекция вектора ( X1, X2, ... Xn, Xn+1) из n+1 пространства,
определяется как вектор ( X1/ Xn+1, X2/ Xn+1, ... Xn/
Xn+1 ) из пространства n измерений.
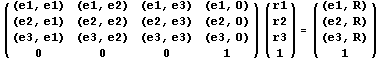
Запишем полученную ранее систему в 4 мерном
пространстве . Логично предположить, что векторы
экранного базиса попарно не параллельны, а
следовательно существует и обратная к
квадратной матрице и следовательно можно
записать :
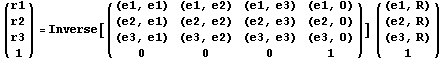 . .
Выражение R-O= r1 e1 + r2 e2+ r3 e3
последовательно умножали на e1, e2, e3
и получили симметрию для подматрицы, но умножать
можно на любую тройку попарно не параллельных
векторов (линейно независимых на языке алгебры) и
получать выражение для вычисления координат
экранного базиса, а следовательно и рисовать.
Например, если используем для скалярного
произведения мировой базис { i, j, k
}, то вместо скалярных произведений в матрице и
векторе правой части соответствующие
коэффициенты будут просто координатами
соответствующих векторов в мировом базисе. Если
экранный базис постоянный и не завистит от
координат объекта, а объект как правило имеет
множество точек, то время вычисления и обращения
матрицы обычно пренебрежимо мало по сравнению с
остальными вычислениями, но на вычислении правой
части возникает экономия, так как ее надо
вычислять многократно.
Используемый прием, замены вектора скалярными
произведениями с целью получения системы
уравнений, или другими словами - замена линейным
функционалом над некоторым пространством
основных векторов, по существу конечномерное
использование обобщенных функций, и имеет
глубокие связи с методом Галеркина или более
широко с методом взвешенных невязок.
В методе конечных элементов обычно не
требуется при изображениях добиваться полной
реалистичности и предыдущей технологии вполне
хватает, но для полноты картины опишем
перспективное отображение, вдруг кто-то захочет
написать игру и потребуется "полная"
реалистичность изображения.
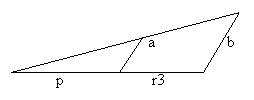
Пусть p расстояние от наблюдателя до экрана, а r3
вычисленная координата, из графики известно, что
если наблюдатель видит предметы одинаковыми, a и b
"сидящие на трубе" в нашем случае, а они
находятся на различном расстоянии от него, то
более удаленный предмет кажется больше близкого.
Аналогичная ситуация и с одинаковыми
предметами "А рельсы то, как водится, у
горизонта сходятся...". Из подобия
треугольников можем записать a/p= b/(p+r3) и
следовательно a=(p/(p+r3))*b. Таким образом, если мы
хотим иметь правильное изображение перспективы,
то каждую из полученных координат точки надо
домножить на (p/(p+r3)) и получим экранные координаты
с учетом перспективы. Такие проективные
преобразования обладают важным свойством – они
являются единственными взаимно однозначными
преобразованиями, которые прямые линии всегда
переводят в прямые линии. При больших p, когда
наблюдатель находится далеко от объектов,
множитель будет стремиться к 1. Если Вам нравятся
однородные координаты то можно просто домножить
полученные ранее экранные координаты на матрицу 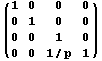 или учесть это
пожелание в более общих процессах вычислений.
Можно придумать и более сложную зависимость
координат в экранном базисе от расстояния
расстояния или (и) угла и понять, например, как
видит мир рыба с большими глазами. Ну и так далее. или учесть это
пожелание в более общих процессах вычислений.
Можно придумать и более сложную зависимость
координат в экранном базисе от расстояния
расстояния или (и) угла и понять, например, как
видит мир рыба с большими глазами. Ну и так далее.
Выше получено достаточно общее выражение для
вычисления координат точки в экранном базисе
через координаты мирового базиса:
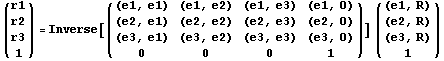
При этом подразумевается, что экранные
базисные вектора описаны в координатах
мирового базиса, так как вектор точки R и
вектор начала координат экрана O описаны в
этом базисе.
Практически можно принять гипотезу о том, что
экран плоский и прямоугольный, по крайней мере
промышленность стремится к этому и,
следовательно, можно предположить, что экран
можно рассматривать, как прямоугольный фрагмент
ориентированной плоскости. Для практического
представления и манипуляций с экранным базисом
будут полезны идеи Германа Грассмана о
плоскостных элементах о которых можно почитать
в замечательной книге Крейна и представить в
виде матрицы
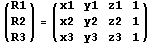
здесь используются три точки, лежащие на
плоскости экрана, при этом будем считать, что 1
точка – это координаты начала экранного базиса.
Пусть e2=R2-R1 и совпадает с горизонтальным
направлением экрана, тогда направление 3 оси
экранного базиса можно определить, как
ортоганальное плоскости экрана, через векторное
произведение, а затем найдем базисный вектор
экрана в вертикальном направлении, при этом
установим согласованные длины базисных
векторов:
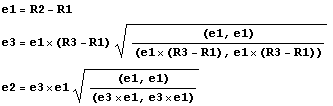
Для возможности использования векторного
произведения здесь 4 координату опустим, так как
используются разности векторов, а в них она
тождественный 0. Простая проверка показывает
ортогональность построенного базиса, в силу
того, что матрица Грама диагональная.
 и вот результаты этих вычислений
и вот результаты этих вычислений
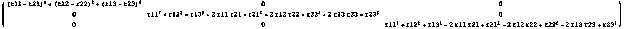
В силу ортогональности построенных базисных
векторов внедиагональные элементы в подматрице
будут нулевыми и ее обращение легко осуществить
явно, скалярное произведение будем обозначать
через нижнее подчеркивание для удобства
манипулирования в программе символьных
вычислений. Учтем, что вместо O начало
экранной системы координат теперь обозначается R1
и вектор из скалярных произведений вектора
произвольной точки мирового пространства на
вектора экранного базиса можно представить в
виде:
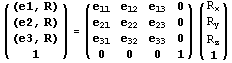 . .
Тогда основное соотношение
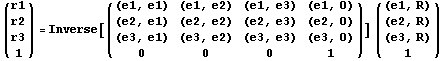 можно представить в виде можно представить в виде
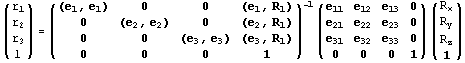 и вычислить в одной из возможных
форм: и вычислить в одной из возможных
форм:
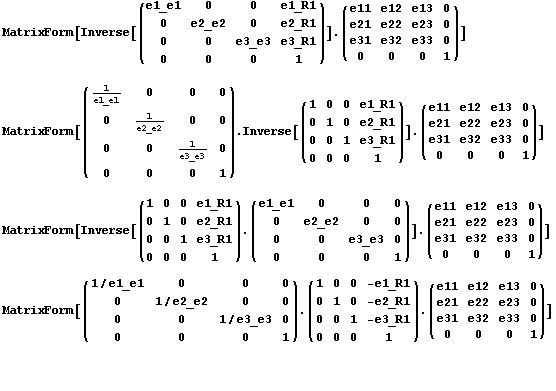 , ,
которые естественно дают одинаковый результат 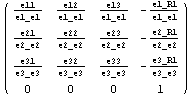 для матрицы преобразования к
экранному базису. для матрицы преобразования к
экранному базису.
Теперь можем записать вычисление координат
произвольной точки в экранном базисе через
линейное отображение координат точки в
мировом базисе в более технологичном виде:
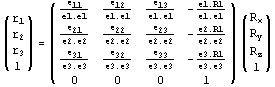 . .
Для проверки и исследования свойств полученной
матрицы, как обычно, воспользуемся программой
символьных вычислений. Оформим вычисление
матрицы преобразования в виде функции, алгоритм
которой будет таким - сначала по трем точкам
экрана строим ортонормальный базис,
масштабируем его в соответствии с желательной
длиной в мировых координатах затем вычисляем
коэффициенты матрицы. Заодно предусмотрим
возможность нарисовать реалистичные
изображения учитывающие перспективу:

Сначала проверим тождественное
преобразование, оно должно получиться если
описать треугольник в плоскости XY с первой
нулевой точкой и единичными по ортам
координатами двух других точек: 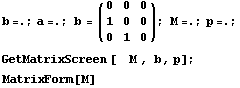
=> 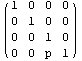 , все правильно. Теперь ориентированный
треугольник развернем в другую сторону , все правильно. Теперь ориентированный
треугольник развернем в другую сторону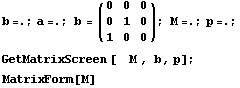 => =>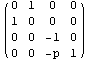 , тоже логично X и Y
меняются местами, а Z напрявляется в другую
сторону. , тоже логично X и Y
меняются местами, а Z напрявляется в другую
сторону.
Теперь если мы научимся управлять тремя
точками плоскости экрана, то сможем и изображать
любой объект, описанный в мировой системе на
экране.
Вращение или поворот это такое движение, при
котором по крайней мере одна точка объекта
остается неподвижной. Для более строгого
определения необходимо исключить деформации,
тогда вращение - это такое преобразование,
которое сохраняет расстояния между точками,
углы между прямыми (векторами) и ориентацию для
плоскостей (или векторное произведение для
векторов). Если вращение описывается линейным
отображением, то неподвижными будут уже две
точки, а следовательно и все точки лежащие на
линии, соединяющей эти точки. Эта линия
называется осью.
Таким образом, под осью будем понимать
произвольную ориентированную прямую линию в
пространстве. Практически мы можем задать ее с
помощью двух точек, и принять за положительное
направление движение от первой точки ко второй,
или задать одну точку A, лежащую на прямой, и
свободный вектор направления n, который не
умаляя общности можем считать единичной
длины. В противном случае просто нормируем его,
то есть разделим координаты на длину. Понятно,
что представление оси в виде двух точек легко
преобразовать к представлению в виде точки и
направления и наоборот.
Сначала рассмотрим вспомогательную задачу.
Пусть ось задана точкой на линии A и свободным
вектором направления n, и задана еще
произвольная точка пространства вне оси R.
Через эту произвольную точку можно провести
плоскость перпендикулярную вектору направления.
Задача: найти точку P пересечения этой
плоскости и оси.
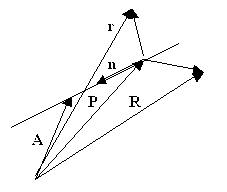
Вектор R-P ортогонален n, так как лежит в
плоскости ортогональной оси, а направление
вектора A-P совпадает с направлением
вектора n. Эти условия можно записать
следующим образом: 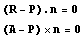 следовательно следовательно 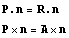 . Напомним формулу для двойного векторного
произведения из векторной алгебры
. Напомним формулу для двойного векторного
произведения из векторной алгебры 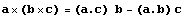 .
Векторно умножим слева последнее соотношение на n
и воспользуемся формулой для двойного
произведения .
Векторно умножим слева последнее соотношение на n
и воспользуемся формулой для двойного
произведения 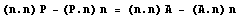 и, учтя первое
соотношение, получим искомое выражение для точки
пересечения оси и плоскости вращения и, учтя первое
соотношение, получим искомое выражение для точки
пересечения оси и плоскости вращения 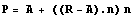 . Эту точку
будем называть точкой вращения. В принципе можно
было бы и догадаться, что к вектору A надо
добавить вектор длиной R-A и направлением
обратным n, но подобную схему решения
векторных уравнений будем использовать в более
сложных случаях и технологию лучше увидеть на
простой и полезной задаче. Приведенное выше
выражение показывает, что координаты точки
вращения являются линейными функциями
относительно координат вращаемой точки и
следовательно оператор, определяемый этими
функциями имеет матричное представление.
Получим его: . Эту точку
будем называть точкой вращения. В принципе можно
было бы и догадаться, что к вектору A надо
добавить вектор длиной R-A и направлением
обратным n, но подобную схему решения
векторных уравнений будем использовать в более
сложных случаях и технологию лучше увидеть на
простой и полезной задаче. Приведенное выше
выражение показывает, что координаты точки
вращения являются линейными функциями
относительно координат вращаемой точки и
следовательно оператор, определяемый этими
функциями имеет матричное представление.
Получим его:
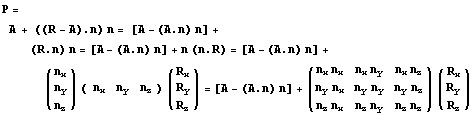 . .
Отметим, что квадратная матрица, это по
существу матрица Грама для вектора оси вращения.
В однородных координатах это будет иметь
следующий вид: 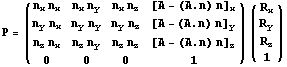 . .
Вращение точки R на положительный угол
вокруг ориентированной оси будет
осуществляться в плоскости ортогональной n
и в соответствии с правилом буравчика. Пусть r
положение точки R после вращения вокруг оси.
Введем обозначения для векторов радиусов
вращения a=R-P, b=r-P, а квадрат длины этих
векторов обозначим буквой d, по существу это
квадрат радиуса вращения. Тогда в соответствии с
определением векторного и скалярного
произведения векторов можем записать систему
векторных уравнений: 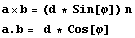 , из решения этих
векторных уравнений найдем b и сможем
записать новое положение точки после вращения r=P+b
в мировой системе координат. Для решения
системы снова умножим верхнее соотношение
векторно на a и, как и ранее, воспользуемся
формулой для двойного векторного произведения , из решения этих
векторных уравнений найдем b и сможем
записать новое положение точки после вращения r=P+b
в мировой системе координат. Для решения
системы снова умножим верхнее соотношение
векторно на a и, как и ранее, воспользуемся
формулой для двойного векторного произведения 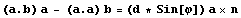 и учтя последнее соотношение
системы получим и учтя последнее соотношение
системы получим 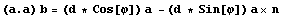 . Учтем, что квадрат длины
радиуса вращения равен . Учтем, что квадрат длины
радиуса вращения равен 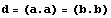 можем сократить
и получим решение системы относительно b>: можем сократить
и получим решение системы относительно b>: 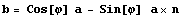 . Теперь можно найти в мировой
системе координат вектор нового положения точки
после вращения на произвольный угол фи вокруг
произвольной оси, для этого сначала выпишем
вместе основные полученные соотношения: . Теперь можно найти в мировой
системе координат вектор нового положения точки
после вращения на произвольный угол фи вокруг
произвольной оси, для этого сначала выпишем
вместе основные полученные соотношения:
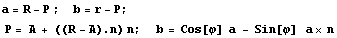
На основе этих соотношений выразим вектор
точки после вращения через характеристики
оси угла поворота и вектора точки до вращения.
При этом учтем, что векторное произведение
вектора на самого себя равно нулю:
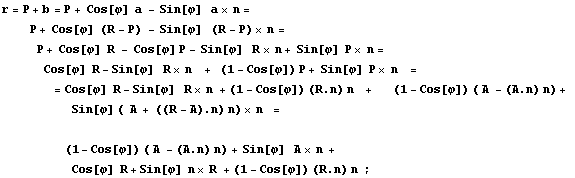
Полученное выражение является линейным
отображением R в r и следовательно может
быть представлено в матричном виде. Первые два
слагаемых по существу вектор, зависящий только
от оси, рассмотрим матричное представление
членов, зависящих от R:
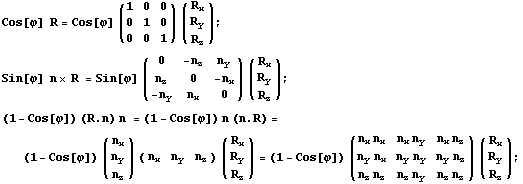
Собрав все вместе, несложно представить это в
виде линейного отображения в 4 мерном
пространстве
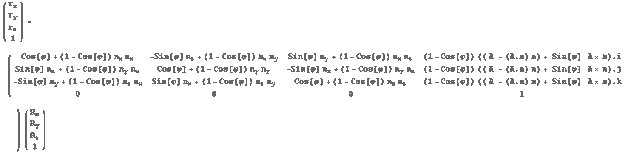
Выражение выглядит несколько громоздким, но
при программировании описать 12 элементов
матрицы не представляет никакого труда, зато мы
сразу имеем возможность описать любое вращение.
Для полного описания возможных движений
твердого тела в пространстве, обычно
назаваемых собственными движениями или
движениями сохраняющими длины, углы и
ориентацию, или для двух произвольных векторов
не лежащих на одной прямой сохраняющих скалярное
и векторное произведения, еще надо иметь
возможность смещать его в заданном направлении.
Это совсем просто r = R + S , где S свободный
вектор, который надо добавить к исходным
координатам. Таким образом полностью
собственные движения твердого тела могут быть
описаны формулой:
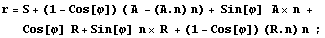
Для матричного представления надо просто
добавить в крайний правый столбец
соответствующие координаты вектора S.
Для проверки и исследования свойств полученных
соотношений воспользуемся программой
символьных вычислений. Сначала оформим
вычисление матрицы собственных движений в виде
функции:

Проведем небольшую проверку с помощью
следующего фрагмента:

и получим
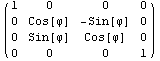 , , 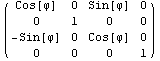 , , 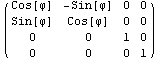 , , 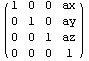
Сравнив полученные матрицы вращения, например,
с данными из популярного справочника по
математике Корнов, убедимся в правильности
результатов при вращении вокруг координатных
осей. Полученная векторная формула, или
соответствующая ей матрица реализуют вращение
вокруг произвольной оси и смещение, но
геометрически можно представить две ситуации:
сначала поворачиваем, а потом смещаем, или
наоборот. Равосильны ли эти ситуации? Другими
словами коммутативны ли операции вращения и
смещения, и какое движение реализует общая
формула?
Проведем небольшой вычислительный
эксперимент:

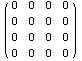
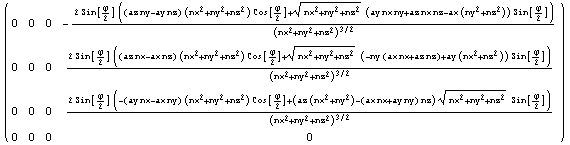
Из этого эксперимента следуют два вывода. Во
первых, операции вращения и смещения не
коммутативны, то есть надо следить за
последовательностью движений, а во вторых общая
операция в виде линейного отображения с помощью
векторной формулы или матрицы эквивалентна
следующим двум: сначала повороту, а затем
смещению.
Вращения вокруг оси и смещения на вектор
позволяют расположить объект в любой области
пространства, что позволяет рассмотреть его с
любых сторон или сделать игру типа
"леталки". Но в программах метода конечных
элементов геометрические преобразования можно
использовать для создания моделей и
постановки краевых условий в виде ограничений
типа линейных соотношений между степенями
свободы, поэтому полезно рассмотреть еще два
линейных преобразования. Сначала рассмотрим
образ, который возникает в результате
зеркального отражения относительно
произвольной плоскости в пространстве.
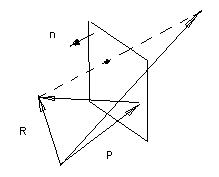
Расстояние от точки R до плоскости
определенной нормированным свободным вектором n
и точкой P, через которую проходит
плоскость отражения, легко определить из
картинки (R-P).n. Теперь несложно записать и
координаты зеркального образа точки: r = R –2
((R-P).n) n , или в виде матричном виде:
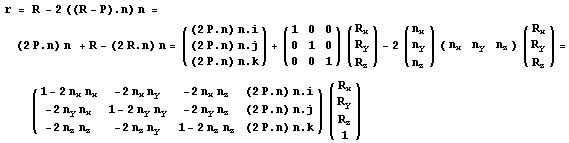
Добавив строчку {0 0
0 1} в матрицу преобразования, получим
линейное отображение в проективном
пространстве.
И еще одно линейное преобразование, обычно
называемое масштабированием, которое можно
рассматривать как расширение понятия
зеркального отражения. Сначала формально
заменим множитель –2 на параметр альфа:
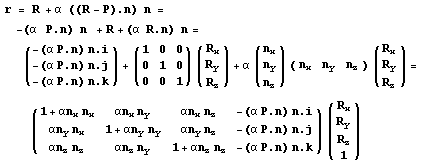
Раз уж мы назвали операцию масштабированием, то
здравый смысл и географические карты требуют,
чтобы было число M называемое масштабом и при
значении М=1 ничего не менялось, поэтому заменим
альфа на M-1 и запишем окончательный результат:
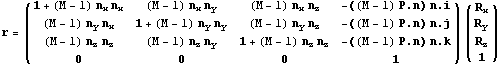
Как и ранее для проверки и исследования свойств
полученных соотношений воспользуемся
программой символьных вычислений. Сначала
оформим вычисление матрицы масштабирования
относительно произвольной плоскости в виде
функции и для совпадения параметров с функцией
вращения добавим возможность смещать
координаты:

Сначала проверим масштабирование относительно
координатных плоскостей:

Результат вполне совподает с ожидаемым:
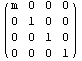 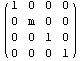 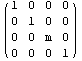 . .
Аналогичная ситуация будет и с зеркальным
отражением относительно координатных
плоскостей если положить m=-1.
Полезно проверить и общий вид:
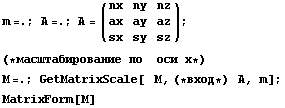

Результат вполне совпадает с ожидаемым если
учесть, что в знаменателе условие нормировки
вектора задающего плоскость.
Для метода конечных элементов удобно размещать
точку на прямой в середине объекта и вращать
вокруг базисных векторов экрана, при этом
возникает интуитиво понятная для человека
активная ситуация, когда он управляет вращением
объекта в горизонтальной, вертикальной
плоскостях и в плоскости экрана. Понятно, что
эту точку можно смещать и тогда будет смещаться
ось вращения. Но в некоторых ситуациях
может оказаться более наглядной игровая точка
зрения, когда наблюдатель "летает или ездит"
вокруг объекта. По сути это одно и то же.
Соберем воедино рассмотренные выше технологии
и поэкспериментируем на практическом рисовании
трехмерных объектов на примере обычного
квадратичного элемента, который подробно изучен
в предыдущих статьях. Сначала для проверки
используем стандартные средства рисования
системы символьных вычислений, так, как
использовали в предыдущих статьях:
Напишем функцию, которая рисует объект,
описанный координатами в мировом пространстве
на основе преобразования к экранным координатам
виртуального экрана через матрицу линейного
преобразования:

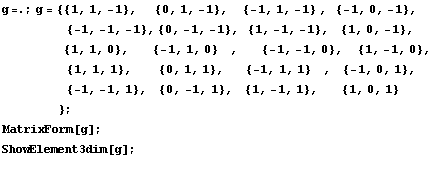

Теперь можем приступить к экспериментам
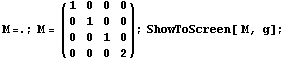 => =>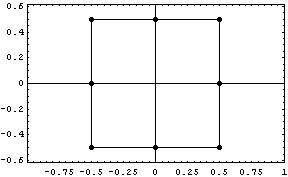 , вполне логично,
нарисовали сечение по двум первым координатам, а
2 используется для масштабирования, хотя можно
было бы и просто увеличить mx или другими
словами образ экрана в мировом базисе. , вполне логично,
нарисовали сечение по двум первым координатам, а
2 используется для масштабирования, хотя можно
было бы и просто увеличить mx или другими
словами образ экрана в мировом базисе.
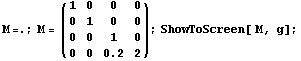 => => 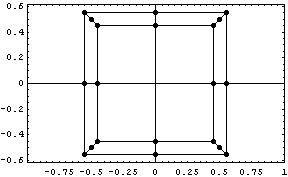 , а это уже перспектива,
передняя стенка увеличилась, задняя уменьшилась,
а точки на серединах боковых граней сохранили
координаты. Теперь опишем плоскость экрана с
помощью треугольника, координаты которого
разместим по строкам матрицы X, а перспективу
зададим с помощью 0.5. , а это уже перспектива,
передняя стенка увеличилась, задняя уменьшилась,
а точки на серединах боковых граней сохранили
координаты. Теперь опишем плоскость экрана с
помощью треугольника, координаты которого
разместим по строкам матрицы X, а перспективу
зададим с помощью 0.5.
 => => 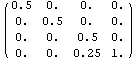
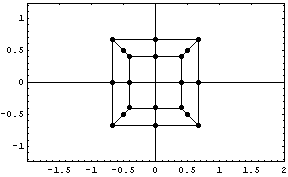 . .
Все логично, раз задали больший размер экрана, в
горизонтальном направлении, то размер
изображения уменьшился и также можно заметить,
что "расстояние между шпалами по мере удаления
от наблюдателя визуально уменьшается".
Будем вращать и смещать треугольник,
описывающий экран и менять его размеры
одновременно:
 = > = >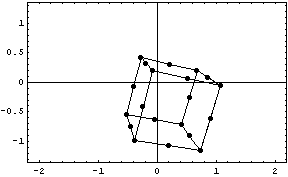 . .
Нет проблем.
А вот, что происходит с аналогичной
"функцией зазеркалья" 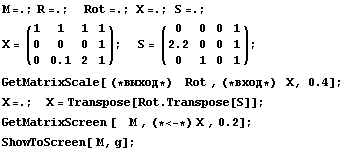 => => 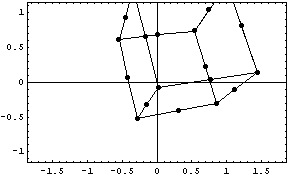
Ну, на этом пожалуй можно и остановиться и
подвести некоторые итоги и наметить новые
задачи.
С помощью всего одной функции можем
организовать проекцию любой точки на плоскость
экрана, описанной с помощью треугольника.
Добавив еще одну функцию, можем организовать
движение экрана, а значит двигаться и
рассматривать виртуальный мир с любой точки
зрения или крутить его вокруг себя, если Вам
нравится эгоцентрическая точка зрения. Добавив
еще одну функцию можно заглянуть к Алисе и узнать
на что "истопник то и открыл глаза"
героям популярной студенческой песни. При этом
достаточно тем или иным способом уметь ставить
точку в заданном месте экрана.
Отметим, что при выводе соотношений
относительно базисов принималось только
предположение об ортогональности и практически
не использовался мировой базис, а это означает,
что по этим формулам можно строить цепочку
отображений из одних ортогональных базисов в
другие и организовать движение их относительно
друг друга, подобно тому как это сделано в Direct3d и
изображать относительные движения при
геометрическом моделировании. Ну, это по
аналогии: лучше один раз увидеть, чем семь раз
услышать; лучше один раз пощупать, чем семь раз
увидеть, и так далее… .
Пока остается в стороне еще очень
интересная и очень полезная обратная задача о
восстановлении трехмерного образа по
произвольным проекциям.
Не рассмотрены и вопросы связанные с
раскраской граней элементов в соответствии с
произвольной функцией от координат, имеющие
большое практическое значение, но в них
математики немного, в основном это вопросы
искусства программирования. В начале этой статьи
упоминался наблюдатель, в чем его роль? Кто-то
должен принимать решения как управлять экранным
треугольником, хотя можно организовать и без
него. В хранителях экрана движение вроде
организовано без наблюдателя, хотя этого никто
не видел…, да и пиво кончается, а без горючего
даже русские танки не ездят, поэтому все эти
интересные проблемы рассмотрим в следующих
статьях.
- Дьяконов В.П. Системы символьной математики
Mathematica 2 и Mathematica 3:-М.:СКпресс,1998
- Капустина Т.В. Компьютерная система Mathematica 3.0 для
пользователей:-СОЛОН-Р,1999
- Клейн Ф. Элементарная математика с точки зрения
высшей. Геометрия. т. 2:М.:Наука,1987
- Корн Г.,Корн Т. Справочник по математике для
научных работников и инженеров:М.:Наука,1974
- Кочин Н.Е. Векторное исчисление и начала
тензорного исчисления: М.:АН СССР,1961
- Тихомиров Ю. Программирование трехмерной
графики:СПб.:BHV,1998
- Томпсон Н. Секреты программирования трехмерной
графики для Windows 95:СПб.:ПИТЕР,1997
Санкт-Петербург, апрель-май 2001
В начало |

