© Ф.Пинежанинов

В начало
Зеркало: http://pinega.da.ru/

• Влияние особенностей интегрируемых  функций
• Численное интегрирование для двухмерных элементов
• Численное интегрирование для трехмерных элементов
• Заключение
• Литература

Влияние особенностей интегрируемых  функций

При практическом написании программ для метода конечных элементов важен вопрос о определении коэффициентов матриц, связанных с квадратичным функционалом. Собственно ради этого и придуман метод конечных элементов, чтобы спроектировать идеи анализа на алгебраические методы.   Эти матрицы называются в теории упругости матрицей жесткости и матрицей масс и коэффициенты этих матриц определяются через кратные интегралы по области конечного элемента . Основное достоинство параметрических конечных элементов заключается в том, что в силу параметрического представления функций, входящих под знак интеграла, интегрирование по криволинейным областям, мы можем заменить интегрированием по области базового конечного элемента, достаточно простой, кубике или треугольной призме, обычно. При этом естественно изменяется подинтегральное выражение. Подинтегральные функции, которые по сути, являются плотностью энергии в физике, сложны, а после параметрических преобразований в них появляются еще якобиан и матрицы Якоби, и они становятся еще сложнее, поэтому для их вычисления   обычно используется  технология численного интегрирования. Поэтому встают два вопроса: сколько узлов численного интегрирования надо использовать,  и, если из-за искажений конечного элемента знак якобиана меняется внутри элемента, то как это может сказаться на точности вычислений, не выбросим ли мы ребенка выливая воду из ванночки.  

При рассмотрении второго вопроса будем придерживаться идеи, которую С.Л. Соболев назвал идеей исключения особенностей и соответственно интеграл будем понимать в смысле теории интеграла Лебега. 

В предыдущих статьях в качестве скалярного произведения  использовали интеграл вида

,

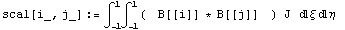если смотрели на базисные функции как на элементы пространства непрерывных функций С0  , и интеграл вида

если смотрели на базисные функции как на элементы пространства  функций  непрерывных со своими производными С1.  Здесь B[[ i ]] список, или вектор  базисных функций.  В силу аддитивности, последний интеграл можно рассматривать как сумму первого и интеграла только из произведений производных

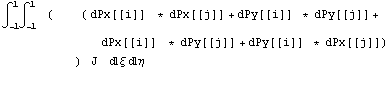
В треугольниках и трехмерных элементах ситуация аналогичная, разница в пределах интегрирования и (или) числе неизвестных, поэтому для качественного анализа ограничимся квадратиком.

Кроме того нет необходимости рассматривать и суммы под знаком интеграла и еще упростим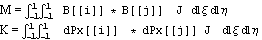    

Матрицы, используемые в конкретных  приложениях по структуре  подобны этим, поэтому изучим эти матрицы и, далее, основные качественные результаты распространим на все остальные. 

Знак якобиана связан с ориентацией области базового элемента и его образа или конкретного элемента. Если положителен значит ориентации совпадают, а если отрицателен, то ориентации различные. Не снижая общности будем считать, что все базисные конечные элементы имеют положительную ориентацию, то есть узлы базисного элемента в правой системе координат занумерованы в согласии с правилом правого винта или штопора, если Вам нравится вино, а не пиво. 

Если знак якобиана отрицателен, то можем просто перенумеровать узлы элемента и сделать его положительным, или проще, просто  брать якобиан по абсолютной величине. Это хорошо, правила движения симметричны относительно правостореннего или левостороннего движения и проблем не будет ни во Франции ни в Англии. Но есть еще и граница.  

Рассмотрим модернизированный интеграл 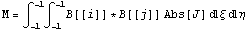,базисные функции – это полиномиальные функции и, следовательно, гладкие для знакопостоянных якобианов. Пусть якобиан меняет знак внутри области интегрирования, следовательно подинтегральная функция имеет излом. Не снижая общности рассуждений будем считать, что якобиан обращается в нуль на одной линии. Тогда квадрат можно разбить на три области: область положительного якобиана, область отрицательного якобиана и  эпсилон-окрестность нулевого якобиана с малой толщиной. Вне эпсилон-окрестности подинтегральные функции обычные полиномы и могут быть вычислены точно.

В эпсилон-окрестности Abs[J] мало отличается от нуля и, следовательно, вся окрестность будет давать малый вклад в интеграл, которым можно пренебречь, учитывая аппроксимирующую роль самих базисных функций и существование изломов функций на границах элементов. И ситуация не может качественно измениться. В силу полиномиальной природы, области нулевого якобиана или эпсилон-окрестности всегда будут иметь меру близкую к  нулю по сравнению с областью интегрирования и интегрироваться по этой мере будут почти нулевые функции.   

Рассмотрим более интересный интеграл, связанный с производными от базисных функций: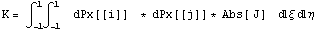 

Сначала проанализируем подробнее получение производных в глобальной системе координат. Пусть функция 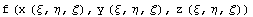,  тогда по правилу дифференцирования сложной функции можно записать:

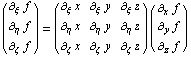.  Квадратная матрица – это матрица Якоби и будем обозначать ее MJ, ее определитель – якобиан преобразования. Так как x, y, z в параметрических элементах полиномиальные функции, следовательни и все алгебраические дополнения матрицы Якоби и сам якобиан будут полиномами. Из алгебры известно, что обратную матрицу можно выразить, через транспонированную матрицу составленную из алгебраических дополнений исходной, деленную на якобиан. Обозначим транспонированную матрицу составленную из алгебраических дополнений матрицы MJ как AMJ и подчеркнем еще раз, что коэффициенты ее полиномы. Обратную матрицу можно записать как AMJ/J и выразить через нее производные в глобальной системе координат:

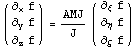 , и еще отметим, что модуль якобиана можно записать в виде: Abs[J]=Sign[J]*J. Теперь структуру интеграла K в трехмерном пространстве от произведений производных можно записать в следующем  виде: 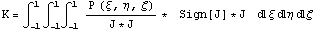, на J можно сократить и получим: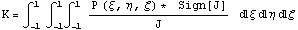.  Снова используем идею выделения особенностей и разобьем интеграл на области без особенностей, в которых якобиан отличен от нуля, и эпсилон окрестность нулевых значений якобиана. В трехмерном пространстве нулевые значения уже образуют поверхность и в силу полиномиальной природы якобиана она будет гладкой.

В направлении ортогональном этой поверхности интеграл будет типа: 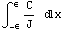, где в числителе можно поставить константу в силу ограниченности непрерывных функций на конечном интервале. Якобиан можно разложить в ряд Тейлора в окрестности нуля в ортогональном направлении и в силу малости эпсилон окрестности ограничится линейным членом. Для понимания поведения интеграла константой можно пренебречь и,  интеграл можно представить в виде 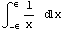 .  Ух, теперь уже недалеко.   Подинтегральная функция кососимметричная, и следовательно интеграл по симметричному интервалу равен нулю, то есть интеграл сходится в смысле главного значения по Коши.

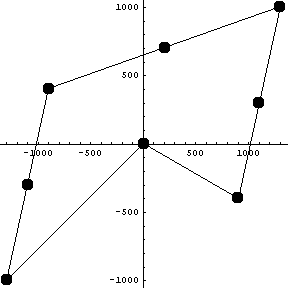
Таким образом, хотя в окрестности нуля функция возрастает неограниченно, но предел справа и предел слева имеют разные знаки и на любом симметричном интервале в интеграле гасят друг друга.

Нарисуем еще и график, для большей убедительности:

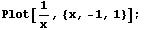
Подведем некоторые итоги. Интегралы обычно используемые в методе конечных элементов могут иметь особенности и ни к каким катастрофическим последствиям это не должно приводить, так как в силу кососимметричного характера подинтегральных функций, интегралы по эпсилон- областям будут иметь нулевую энергию, в смысле обычно приписываемом этим интегралам в математической физике. Процедура вычисления этих интегралов устойчива, в том смысле, что малым изменениям геометрии любого конечного элемента будут соответствовать малые изменения значений интеграла, построенного на базисных функциях и (или) производных и по структуре похожим на определение скалярного произведения в пространстве функций непрерывных со своими первыми производными.

 Для постановок задач, использующих предельный переход типа балок или оболочек, естественно надо еще подобным образом изучить поведение и производных более высокого порядка. Но об этом сейчас не будем. 

  Отметим еще важную для практических вычислений особенность. Если конечный элемент удовлетворяет условию аффинности, то есть может быть отображен на базисный элемент с помощью линейного преобразования, то матрица Якоби, а следовательно и якобиан будут постоянными по всей области интегрирования и якобиан может быть вынесен из под знака интегрирования, а подинтегральное выражение всегда будет полиномом и  может быть вычисленно точно.

 В случае нелинейных отображений под интегралом будет рациональная функция и, хотя в математическом анализе доказано, что  подобные неопределенные интегралы могут быть вычисленны точно, в силу сложности выражений, как и в аффинном случае, обычно используются процедуры численного интегрирования по Гауссу, как наиболее экономичные.

 Автору не известны пригодные для практического использования данные, которые позволяли бы численно и точно вычислять определенные интегралы для рациональных функций, подобно процедурам для полиномов, но математика развивается...

 Оценим на качественном уровне возможное влияние рациональных функций на  кратные интегралы по области конечного элемента. Из алгебры известно, что  если степень полинома  в числителе больше степени полинома в знаменателе и существует  разложение, через деление полиномов, на сумму полинома и рациональную функцию у которой степень числителя меньше степени знаменателя.

 В силу аддитивности интеграла его можно разложить на два: c полиномом и рациональной функцией.  С первым интегралом никаких вычислительных проблем нет и далее сосредоточимся на втором у которого степень полинома числителя меньше степени полинома знаменателя . Из алгебры известно, что такие рациональные функции можно разложить на элементарные дроби  в числителе которых константа, а в знаменателе разность между переменной и корнем якобиана, в рассматриваемом случае. Как влияют на кратный интеграл значения в эпсилон окрестности корней легко понять опираясь на идею исключения особенностей и это уже проанализировано выше, а посмотрев еще раз на график гиперболы можно сделать вывод о том, что вне областей  особенностей даже линейные функции будут хорошо аппроксимировать гиперболы, а тем более уж полиномы более высокого порядка.

 Логически вводя подобным образом аппроксимацию рациональных функций на областях конечного элемента полиномами мы можем быть уверены в успехе численного интегрирования, которое для полиномов при надлежащем выборе числа точек является точным. А в случае знакопостоянных якобианов в области конечного элемента, вообще не о чем беспокоиться. 

 Замена определения скалярного произведения в виде интеграла, определением в виде суммы через численное интегрирование является вполне эквивалентной, если понимать интеграл в смысле Лебега даже в случае особенностей.

 Основной вопрос таким образом в надлежащем выборе точек интегрирования.  При практических вычислениях автор использует такой прием: если абсолютная величина якобиана близка к минимальному значению не равному нулю, то возмущает точку интегрирования до тех пор пока якобиан не примет приличное значение. Применяя разные способы возмущения точки интегрирования, автор убедился, что результаты вычисления интегралов практически не зависят от способа возмущения. По существу это уход с эпсилон окрестностей. Хотя можно воспользоваться теоремой о среднем и за значение интеграла принимать среднее значение на окружности диаметр которой, превосходит диаметр эпсилон окрестности, отбрасывая при этом значения в области нулевого якобиана.      

 В подтверждение вышеизложенного приведем несколько "крамольных" картинок, полученных на программе "Pinega", разработанной автором на основе теории излагаемой в этих статьях.

 Вот вид порождающего сечения, белый цвет элемента показывает, что якобиан внутри области интегрирования меняет знак. На основе этих сечений сгенерированы стерженьки как трехмерные объекты теории упругости.

 Для нижних сечений поставлены условия нулевых смещений, а для верхних сечений смещения по 13 единиц в направлении осей x и y  (13 потому, что автор подобные упражнения называет чертовыми фокусами, наверное как то так выглядел квадратный трехчлен, который не мог продставить себе прославленный полководец   ) . Раскрашено в соответствии с первыми главными напряжениями и теплые цвета соответствуют растяжениям.

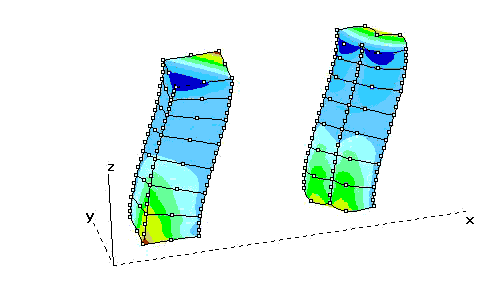
Видите, никаких неожиданностей все вполне соответствует как  излагаемой здесь теории, так и интуитивным представлениям инженера. Но Вы вовсе не обязаны так моделировать, автор просто хотел сказать, что можете, и выбор за Вами.

 Кстати, если, Уважаемый читатель, Вы можете помочь, то замечу, что автору нужны инвестиции для завершения работ по оснащению российских конструкторов лучшим программным обеспечением, ибо только их гений  (инженер - это от ингениус - умный, изобретательный человек) в сочетании с лучшей теорией и программами, может помочь промышленности, а следовательно и многострадальной России. Так же хотелось бы издать эти результаты и на бумаге для стимулирования молодых программистов и математиков.  Благодарность автора будет безграничной, хотя бы в смысле интеграла Лебега. 

А вот подтверждение того, что гиперболическую функцию можно достаточно хорошо представить полиномом, если разложить ее в ряд Тейлора относительно точки удаленной от особенности, на графике показан рост отклонения от гиперболы.

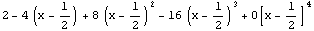
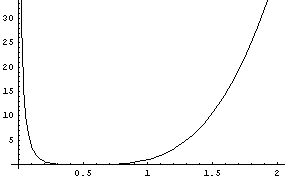
С точки зрения конечных элементов, как отмечал Зенкевич, и не хуже,   что подинтегральная функция в квадратичном функционале будет меньше вычисленной точно. Это будет только немного компенсировать избыточную жесткость из-за конечности конечноэлементных аппроксимаций функционала. Но на это не стоит особо рассчитывать, достаточно понимать, что разумно примененное численное интегрирование не ухудшает ситуации в целом.

На этом обсуждение поведения функций можно закончить и пора ответить на вопрос: сколько же точек интегрирования надо брать, чтобы быть уверенным в результатах вычислений.

 Численное интегрирование для двухмерных элементов

Как и в статье "Свойства изопараметрических конечных элементов" сначала создадим несколько функций для программы "Математика", осуществляющей символьные преобразования, а затем используя технологии построения базисных функций исследуем порядки полиномов, возникающие в методе конечных элементов и  сколько точек интегрирования надо использовать для точного вычисления интегралов при использовании схем Гаусса-Лежандра. Сначала функция рисования элемента:

Еще функция , которая определяет порядок полиномов для якобиана, по каждой переменной, подсчитывает необходимое число точек Гаусса –Лежандра, для точного вычисления кратного интеграла, рисует график якобиана и функции обратной ему, для визуального наблюдения эпсилон-окрестностей нулевого якобиана.

Еще функция с помощью которой будем определять порядок полиномов в числителе подинтегральной функции построенной на произведении производных и порядок функции построенной на произведении базисных функций для изопараметрических конечных элементов .   

Как и в предыдущих статьях построим систему базисных функций на основе исходного полиномиального семейства функций:

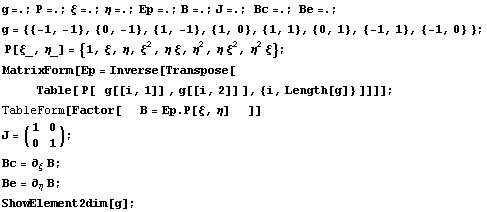
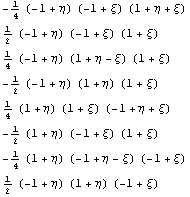
 Далее проверим порядок якобиана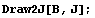

Якобиан =1.

Порядок якобиана по кси =0   точек интегрирования = 1

Порядок якобиана по эта  =0   точек интегрирования = 1

Изображения якобиана и обратной ему функции опустим ввиду очевидности, а определим порядок полиномов, необходимых для точного вычисления интегралов:

Порядок по кси числителя  = 4  точек интегрирования  = 3

Порядок по эта числителя  = 4  точек интегрирования  = 3

Порядок по кси = 4  точек интегрирования  = 3

Порядок по эта = 4  точек интегрирования  = 3

Напомним, еще раз, что первые два предложения относятся к интегралу от произведений производных, а вторые два к интегралу от произведений базисных функций.

Далее исследуем случай аффинного отображения :

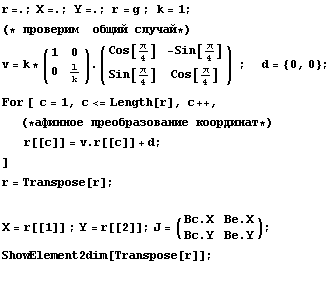
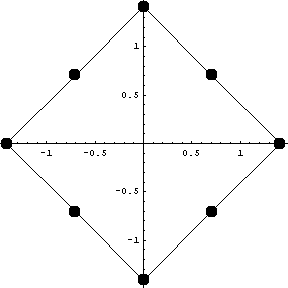
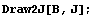
Якобиан =1.

Порядок якобиана по кси =0   точек интегрирования = 1

Порядок якобиана по эта  =0   точек интегрирования = 1

Изображения якобиана и обратной ему функции опустим ввиду очевидности, а определим порядок полиномов, необходимых для точного вычисления интегралов:

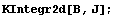
Порядок по кси числителя  = 2  точек интегрирования  = 2

Порядок по эта числителя  = 4  точек интегрирования  = 3

Порядок по кси = 4  точек интегрирования  = 3

Порядок по эта = 4  точек интегрирования  = 3

Видим, что результаты аналогичны базовому. Теперь исследуем влияние чисто изопараметрических возмущений:

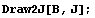
Якобиан =.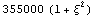

Порядок якобиана по кси =2   точек интегрирования = 2

Порядок якобиана по эта  =0   точек интегрирования = 1

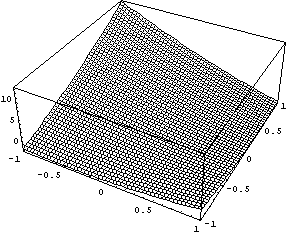
А так выглядит якобиан преобразования и обратная к нему функция.

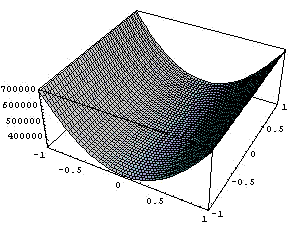
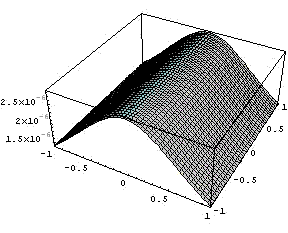
Порядок по кси числителя  = 6  точек интегрирования  = 4

Порядок по эта числителя  = 4  точек интегрирования  = 3

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 4  точек интегрирования  = 3

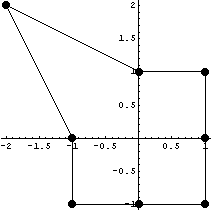
Еще пример гомотопного элемента:

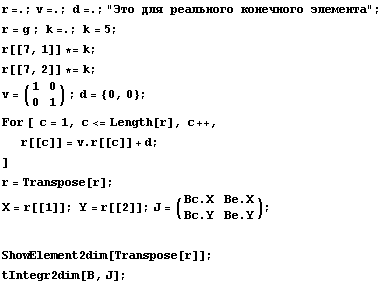
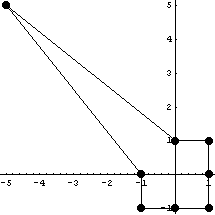
Якобиан =.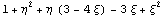

Порядок якобиана по кси =2   точек интегрирования = 2

Порядок якобиана по эта  =2   точек интегрирования = 2

А так выглядит якобиан преобразования и обратная к нему функция.

Порядок по кси числителя  = 6  точек интегрирования  = 4

Порядок по эта числителя  = 6  точек интегрирования  = 4

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 6  точек интегрирования  = 4

И еще одна гомотопия, но уже со знакопостоянным якобианом:

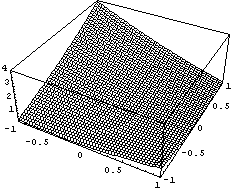
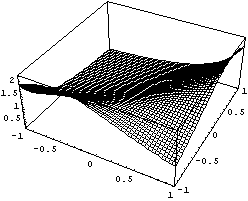
Данные по якобиану и подинтегральным функциям полностью совпадают с предыдущим, просто хотелось показать подробнее функцию обратную якобиану.

Поставлено достаточно много экспериментов, чтобы сделать обоснованные выводы для квадратичных элементов. Для  точного вычисления объемов в общем случае достаточно 2 точек интегрирования по Гауссу на переменную. Для точных вычислений на аффинных элементах интегралов от произведения базисных функций (матрицы масс) достаточно 3 точек на переменную.

Для точных вычислений определенных интегралов от произведения производных на аффинных элементах надо брать тоже по 3 точки на переменную. В случае изопараметрических элементов точно интеграл от рациональных функций не вычислить, но разумно потребовать, чтобы хотя бы полиномиальная часть вычислялась точно и следовательно порядок полиномов будет 6-2=4, а следовательно надо тоже 3 точки интегрирования, при этом можно быть достаточно уверенным в том, что рациональные остатки будут хорошо аппроксимироваться  на удалении от эпсилон-окрестности нулевого якобиана.  Если немного обобщить понятие главного значения интеграла, то можно говорить о точном вычислении кратных интегралов от рациональных функций в смысле главного значения, но вообще то эти случаи входят в теорию интеграла Лебега. Для точного вычисления интегралов от произведений базисных функций для этого случая надо брать по 4 точки интегрирования. Общее количество узлов интегрирования определяется через декартово произведение по переменным. 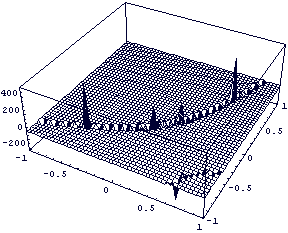Обратите внимание на график обращеного якобиана у элемента с сильно вытянутым узлом, на нем хорошо видны эпсилон-окрестности нулевого якобиана.    Для треугольников надо ориентироваться на порядок полинома 4 и можно использовать результаты из справочника по специальным функциям, руководствуясь степенью полинома, оттуда же можно взять и узлы для кубика,   ошибка будет иметь порядок 6, что соответствует 3 гауссовым точкам. Ниже приведены порядки остаточного члена для гауссовых точек.

Число точек = 1  остаточный член =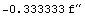

Число точек = 2  остаточный член =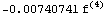

Число точек = 3  остаточный член =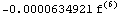

Число точек = 4  остаточный член =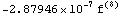

Число точек = 5  остаточный член =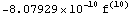

Число точек = 6  остаточный член =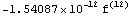

Число точек = 7  остаточный член =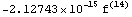

Число точек = 8  остаточный член =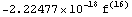

Далее аналогичным образом рассмотрим популярный линейный элемент:

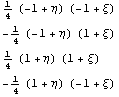
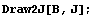
Якобиан = 1.

Порядок якобиана по кси =0   точек интегрирования = 1

Порядок якобиана по эта  =0   точек интегрирования = 1

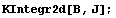
Порядок по кси числителя  = 2  точек интегрирования  = 2

Порядок по эта числителя  = 2  точек интегрирования  = 2

Порядок по кси = 2  точек интегрирования  = 2

Порядок по эта = 2  точек интегрирования  = 2

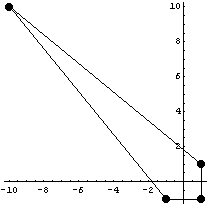
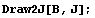
Якобиан = .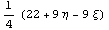

Порядок якобиана по кси =1   точек интегрирования = 1

Порядок якобиана по эта  =1   точек интегрирования = 1

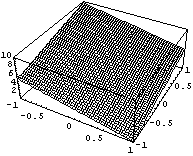
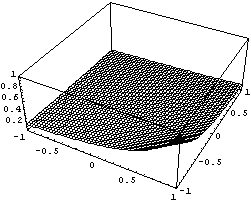
Порядок по кси числителя  = 2  точек интегрирования  = 2

Порядок по эта числителя  = 2  точек интегрирования  = 2

Порядок по кси = 3  точек интегрирования  = 2

Порядок по эта = 3  точек интегрирования  = 2

Для таких элементов  надо брать по 2  точки интегрирования.

Далее исследуем кубичный элемент:

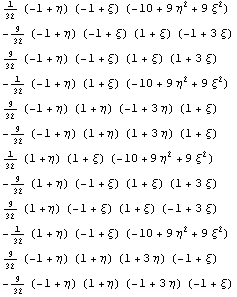
С якобианом в этом случае все понятно.

Порядок по кси числителя  = 6  точек интегрирования  = 4

Порядок по эта числителя  = 6  точек интегрирования  = 4

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 6  точек интегрирования  = 4

Снова случай аффинных пеобразований:

Порядок по кси числителя  = 4  точек интегрирования  = 3

Порядок по эта числителя  = 6  точек интегрирования  = 4

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 6  точек интегрирования  = 4

Вот чисто изопараметрическое преобразование:

Якобиан =.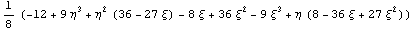

Порядок якобиана по кси =3   точек интегрирования = 2

Порядок якобиана по эта  =3   точек интегрирования = 2

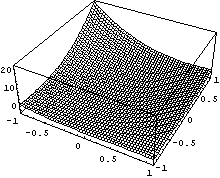
Порядок по кси числителя  = 10  точек интегрирования  = 6

Порядок по эта числителя  = 10  точек интегрирования  = 6

Порядок по кси = 9  точек интегрирования  = 5

Порядок по эта = 9  точек интегрирования  = 5

На последнем графике снова хорошо видна локализация эпсилон-окрестности нулевого якобиана. А следуя ранее изложенным соображениям, порядок полинома  10-2=8  и следовательно можно рекомендовать использовать по 5 узлов интегрирования на переменную при вычислении интегралов от произведений производных, но уж не меньше 4, чтобы точно интегрировать хотя бы аффинные элементы.

Численное интегрирование для трехмерных элементов

В принципе обобщение предыдущих результатов на трехмерный случай не представляет никакого труда на основе декартова произведения, от независимых переменных , однако подинтегральные выражения сложны и проверим на линейно квадратично кубичном элементе. Сначала как обычно подготовим несколько функций для исследования. 

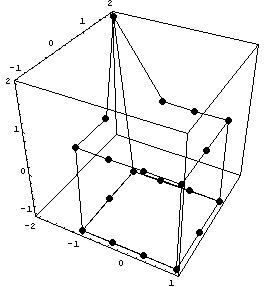
Теперь, используем метод окаймления для построения исходного базиса и на его основе построим конечно-элементные базисные функции:

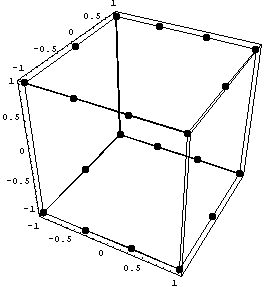
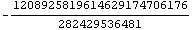
1

Якобиан =1.

Порядок якобиана по кси =0   точек интегрирования = 1

Порядок якобиана по эта  =0   точек интегрирования = 1

Порядок якобиана по дзета     точек интегрирования = 1

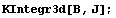
Порядок по кси числителя  = 6  точек интегрирования  = 4

Порядок по эта числителя  = 4  точек интегрирования  = 3

Порядок по дзета числителя  = 2  точек интегрирования  = 2

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 4  точек интегрирования  = 3

Порядок по дзета = 2   точек интегрирования   = 2

Случай аффинного преобразования:

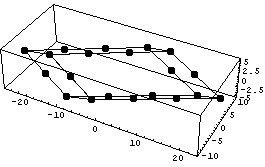
Якобиан =216.

Порядок якобиана по кси =0   точек интегрирования = 1

Порядок якобиана по эта  =0   точек интегрирования = 1

Порядок якобиана по дзета  =0   точек интегрирования = 1

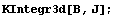
Порядок по кси числителя  = 6  точек интегрирования  = 4

Порядок по эта числителя  = 4  точек интегрирования  = 3

Порядок по дзета числителя  = 2  точек интегрирования  = 2

Порядок по кси = 6  точек интегрирования  = 4

Порядок по эта = 4  точек интегрирования  = 3

Порядок по дзета = 2   точек интегрирования   = 2

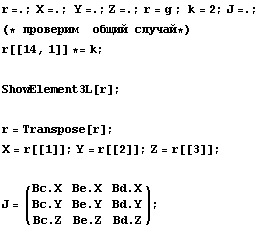
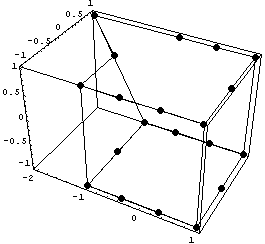
Якобиан =.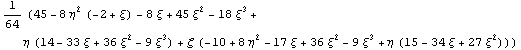

Порядок якобиана по кси =3   точек интегрирования = 2

Порядок якобиана по эта  =2   точек интегрирования = 2

Порядок якобиана по дзета  =1   точек интегрирования = 1

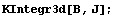
Порядок по кси числителя  = 10  точек интегрирования  = 6

Порядок по эта числителя  = 8  точек интегрирования  = 5

Порядок по дзета числителя  = 4  точек интегрирования  = 3

Порядок по кси = 8  точек интегрирования  = 5

Порядок по эта = 6  точек интегрирования  = 4

Порядок по дзета = 3   точек интегрирования   = 2

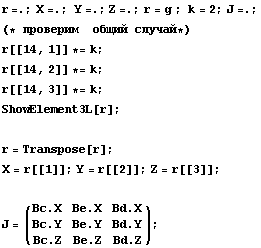
 Якобиан =.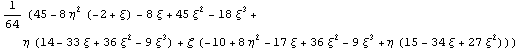

Порядок якобиана по кси =3   точек интегрирования = 2

Порядок якобиана по эта  =2   точек интегрирования = 2

Порядок якобиана по дзета  =1   точек интегрирования = 1

Порядок по кси числителя  = 12  точек интегрирования  = 7

Порядок по эта числителя  = 8  точек интегрирования  = 5

Порядок по дзета числителя  = 4  точек интегрирования  = 3

Порядок по кси = 9  точек интегрирования  = 5

Порядок по эта = 6  точек интегрирования  = 4

Порядок по дзета = 3   точек интегрирования   = 2

Следуя ранее изложенному, потребуем, чтобы полиномы считались точно  порядок полинома 12-3=9  и следовательно можно рекомендовать использовать по 5 узлов интегрирования на  кубическую переменную при вычислении интегралов от произведений производных, по 4 узла на квадратичную переменную и по 2 узла на линейную переменную. При этом интегралы от произведений базисных функций будем вычислять точно, а в интегралах от произведений производных будем точно считать полиномиальную составляющую, и неплохо аппроксимировать гиперболическую составляющую вне эпсилон – окрестности нулевого якобиана.

Заключение

Численное интегрирование практически всегда используется при работе с конечными элементами. На него можно смотреть как на замену функционала в виде интеграла функционалом в виде конечной суммы, или как на аппроксимацию подинтегральной функции полиномом, степени которого определяются числом точек интегрирования, при этом всегда говорим о квадратурах Гаусса-Лежандра, так как другие методы интегрирования крайне редко используются. Для точного вычисления объемов достаточно брать по линейной переменной 1 узел, по квадратичной и кубичной по 2 узла интегрирования. Для точного вычисления в случае аффинных элементов интегралов для матриц масс и матриц жесткости надо брать 2,3,4 узла интегрирования для линейной, квадратичной или кубичной переменной соответственно. Для "точного" вычисления, в смысле описанном в этой статье, автор предпочитает осторожные 3,4,5 для аналогичных ситуаций, чтобы поточнее интегрировать гиперболические остатки, иначе возможно завышение жесткости конечного элемента, а современные компьютеры работают быстро и это не проблема. С другой стороны точнее учитываются области знакопеременных якобианов в экстравагантных случаях, а это может пригодиться в нелинейных задачах. 

Для эрмитовых элементов и иерархических базисных функций несложно исследовать вопросы интегрирования используя технологию этой статьи. В случае затруднений свяжитесь с автором.   

Литература

 Соболев С.Л. Уравнения математической физики: -М.:Наука, 1992.

Стренг Г.,Фикс Дж. Теория метода конечных элементов: Пер. с англ. - М.:Мир, 1977.

Сьярле Ф. Метод конечных элементов для эллиптических задач: Пер. с англ. - М.:Мир, 1980.

Зенкевич О.Метод конечных элементов в технике: Пер. с англ. - М.:Мир, 1975.

Справочник по специальным функциям: Пер. с англ. - М.:Наука, 1979.

Образцов И.Ф.,Савельев Л.М.,Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов: - М.Высшая школа, 1985.

Санкт-Петербург,  февраль 2001 

В начало