|
Задача 6
Постановка задачи
Даны две задачи Коши для систем ОДУ 1 порядка с постоянными коэффициентами на отрезке [0, 1]:




выяснить, какая из задач является жесткой.
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Составить программу-функцию нахождения решения системы ОДУ 1 порядка с постоянными коэффициентами по явному методу Эйлера. Используя составленную программу, решить обе задачи с шагом h=0.01. Определить, для какой из задач явный метод неустойчив при данном шаге h.
2. Используя встроенную функцию eigenvals(M) (M матрица) пакета MathCAD для нахождения собственных чисел матриц A и B, найти коэффициенты жесткости обеих систем. Какая из задач является жесткой?
3. Для жесткой задачи теоретически оценить шаг h*, при котором явный метод Эйлера будет устойчив.
4. Составить программу-функцию нахождения решения системы ОДУ 1 порядка с постоянными коэффициентами по неявному методу Эйлера. Используя составленную программу, найти решение жесткой задачи с шагом h=0.01. Построить графики компонент полученного решения.
5. Для жесткой задачи экспериментально подобрать шаг h, при котором графики компонент решения, полученного по явному методу Эйлера, визуально совпадают с графиками компонент решения, полученного по неявному методу с шагом h=0.01. Сравнить найденное значение шага с шагом h*. Объяснить различие поведения явного и неявного методов Эйлера при решении жесткой задачи.
Необходимый теоретический материал
Жёсткие системы уравнений.
Пусть имеется система уравнений c постоянными коэффициентами:
 |
(*) |
которая имеет устойчивое решение

Если все его компоненты  существенно различаются по скорости своего изменения на промежутке [ существенно различаются по скорости своего изменения на промежутке [ ], на котором решается задача Коши, то применение здесь условно устойчивых численных процессов требует интегрирования с таким малым шагом, какой обеспечивает устойчивое вычисление самой быстрозатухающей компоненты (так как шаг h - это величина скалярная, общая для всех компонент). Следовательно, жесткость системы ДУ зависит от того, насколько сильно отличается поведение компонент вектора-решения при условии его асимптотической устойчивости. В свою очередь, в случае постоянной матрицы А в системе (*) это различие в скорости изменения функций ], на котором решается задача Коши, то применение здесь условно устойчивых численных процессов требует интегрирования с таким малым шагом, какой обеспечивает устойчивое вычисление самой быстрозатухающей компоненты (так как шаг h - это величина скалярная, общая для всех компонент). Следовательно, жесткость системы ДУ зависит от того, насколько сильно отличается поведение компонент вектора-решения при условии его асимптотической устойчивости. В свою очередь, в случае постоянной матрицы А в системе (*) это различие в скорости изменения функций  связано с тем, насколько сильно отличаются собственные числа связано с тем, насколько сильно отличаются собственные числа  матрицы А. Отсюда вытекает определение жесткой системы: матрицы А. Отсюда вытекает определение жесткой системы:
Система (*) с постоянной n x n - матрицей А называется жесткой, если собственные числа  (k=1,2,...,n) матрицы А удовлетворяют следующим условиям: (k=1,2,...,n) матрицы А удовлетворяют следующим условиям:
1) 
2) Число жесткости 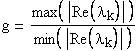 велико. велико.
Зададим исходные данные:
Матрица системы:


Начальные условия:


Концы отрезка:


Опишем функцию нахождения решения системы ОДУ 1 порядка c постоянными коэффициентами по явному методу Эйлера:
Описанная программа-функция, подобно встроенным функциям rkfixed, stiffb и др., возвращает таблицу решений, первый столбец которой - это значения аргумента в узлах равномерной сетки, а остальные столбцы - соответствующие значения компонент приближенного решения.

Решим обе системы по явному методу Эйлера с шагом h = 0.01:
Зададим векторы правых частей систем уравнений:







Графики решений для первой системы:


Графики решений для второй системы:


Определим, для какой из задач явный метод неустойчив при данном шаге h = 0.01.
Для нахождения жесткости системы и для определения неустойчивости явного метода Эйлера воспользуемся встроенной функцией eigenvals для нахождения собственных чисел матриц систем А и В.




Максимальные и минимальные собственные числа матриц:












Как видно, условие устойчивости выполняется для матрицы B (usB > h), но не выполняется для матрицы A (usA < h). Следовательно, явный метод Эйлера неустойчив для решения системы, описанной матрицей A.
Определим, какая из систем является жесткой:




Число жесткости системы gB мало (т. е. собственные числа матрицы B незначительно отличаются друг от друга), поэтому система не жесткая.
Число жесткости системы gA велико (т. е. собственные числа матрицы A значительно отличаются друг от друга), поэтому система жесткая.
Определим, при каком шаге h = h*, явный метод Эйлера будет устойчив при решении жесткой системы:




Графики решений для первой и второй компоненты систем:


Как видно из графиков решений, явный метод Эйлера устойчив с шагом h = 0.002 . Условие устойчивости  ( ( ). выполняется (см. выше). ). выполняется (см. выше).
Найдем решение жесткой задачи по неявному методу Эйлера:
Опишем функцию нахождения решения системы ОДУ 1 порядка c постоянными коэффициентами по неявному методу Эйлера:
Описанная программа-функция возвращает таблицу решений, первый столбец которой - это значения аргумента в узлах равномерной сетки, а остальные столбцы - соответствующие значения компонент приближенного решения.
В качестве параметров она принимает матрицу М системы, вектор начальных условий Vo начало to , конец отрезка интегрирования T и число узлов равномерной сетки N:

Для оценки результатов решения будем использовать встроенную функцию для решения жёстких систем stiffr. Для её применения необходима матрица Якоби:


Решим жесткую систему по неявному методу Эйлера с шагом h = 0.01:





Графики решений для первой и второй компоненты систем:


Найдем такое значение шага H для решения жесткой системы по явному методу Эйлера, что результаты решения будут визуально совпадать с решением, полученным неявным методом Эйлера с шагом h = 0.01:






Так как неявный метод тоже обладает некоторой погрешностью, то при дроблении шага H, дальнейшего приближения решения, полученного явным методом, к решению неявным методом, не произойдёт.
Вывод: явный метод Эйлера 1-го порядка точности дает приближённое решение систем ОДУ с постоянными коэффициентами. При решении жестких систем ОДУ, метод может быть неустойчив при достаточно большом шаге вычислений. При уменьшении шага вычислений метод будет устойчив, но это требует дополнительных (на некотором промежутке лишних) вычислений.
Путем простой модификации явного метода Эйлера, можно получить неявный метод Эйлера c абсолютной устойчивостью. Приемлемое устойчивое решение, получаемое при решении жёсткой системы уравнений чисто неявным методом, требует в несколько десятков раз меньше итераций, чем решение, полученное по явному методу Эйлера.
|

