|
Задача 2
Постановка задачи
Задача Коши для ОДУ 2-го порядка:
t  [ 0; T ]
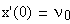
описывает движение груза массы m, подвешенного к концу пружины. Здесь x(t) смешение груза от положения равновесия, H - константа, характеризующая силу сопротивления среды, k - коэффициент упругости пружины, f(t) - внешняя сила. Начальные условия: x0 - смешение груза в начальный момент времени t0,  0 - скорость груза в начальный момент времени. Промоделировать движение груза на временном отрезке [0; T] при заданных трёх наборах (I, II, III) значений параметров задачи. Для каждого набора по найденной таблице или графику решения задачи определить максимальное и минимальное значения функции f(t) и моменты времени, в которых эти значения достигаются.
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1. Заменить исходную задачу эквивалентной задачей Коши для системы ОДУ 1 порядка:
2. Для каждого варианта выбора параметров решить задачу с помощью метода Рунге-Кутты 4 порядка точности с шагом h=0.1.
3. Для каждого варианта выбора параметров построить график найденного решения. Сравнить характер движения груза и дать интерпретацию полученного движения.
4. Для каждого варианта выбора параметров определить требуемые в задаче характеристики.
УКАЗАНИЕ. В п. 2 использовать встроенную функцию rkfixed пакета MathCAD.
Необходимый теоретический материал
Численное решение систем дифференциальных уравнений первого порядка.
Пусть требуется найти решение задачи Коши для системы обыкновенных дифференциальных уравнений первого порядка, разрешенных относительно производных:
.....................
.....................................
Введем следующие векторные обозначения:
   
С ними данная задача Коши принимает вид:
Легко понять, что к векторному дифференциальному уравнению, в принципе, можно применить любой из численных методов.
При этом скалярными величинами в формулах, определяющих методы, являются только независимая переменная x и расчетный шаг h; всем остальным величинам соответствуют введенные выше векторы размерности n. Следует лишь учесть, что при контроле точности вместо модуля нужно использовать норму вектора (например, норму-максимум).
Задача Коши для любого дифференциального уравнения n-го порядка легко сводится к задаче для системы дифференциальных уравнений порядка n: , где
  
Решение:
Дано:
Уравнение движения:
Интервал времени:
Шаг сетки интегрирования:
Число узлов сетки:
Набор параметров, которые не изменяются:
Так как это ДУ 2-го порядка, то сведём его к системе ДУ:
Первый изменяющийся набор параметров:
Преобразуем начальные значения - координату и скорость - к векторному представлению:
Преобразуем исходное уравнение 2 порядка в эквивалентной нормальной системе уравнений первого порядка, и представим её в форме вектора:
Решим систему методом Рунге-Кутты 4-го порядка:
Второй изменяющийся набор параметров:
Третий изменяющийся набор параметров:
Результаты решений представим в виде графиков. Кроме того, найдём минимальные и максимальные значения полученных решений для каждого набора данных и значения аргумента (времени), когда эти значения достигаются.
Для определения экстремумом воспользуемся встроенными функциями min и max, а для определения значений аргумента - встроенным средством Trace.
Для первого случая:
В первом случае происходит затухание колебаний - груз постепенно останавливается.
Максимальное значение амплитуды:
Минимальное значение амплитуды:
Для второго случая:
Подобно первому случаю, колебания затухают. Но отличие состоит в том, что небольшая, по сравнению с первым случаем, жёсткость пружины, влияющая на силу сжатия и растяжения пружины, не позволяет пружине преодолеть силу сопротивления среды, поэтому сжатия пружины не происходит - значение функции всегда положительно. (Предполагается, что положительное направление оси Х - в сторону растяжения пружины)
Максимальное значение амплитуды:
Минимальное значение амплитуды:
Для третьего случая:
Набор параметров подобран таким образом, что затухающие колебания происходят поодобно математическому маятнику - сопротивление среды останавливает со временем движение груза, происходящее по гармоническому закону.
Максимальное значение амплитуды:
Минимальное значение амплитуды:
Вывод: дифференциальные уравнения второго порядка - часто употребительный способ описания движения. Численное решение этих дифференциальных уравнений, ввиду их сложности, порой единственный способ нахождения закона движения. Но простота вычислений с применением системы MathCAD - это быстрый путь к решению проблемы.
| 
