Задача 1

Постановка задачи

Найти приближенное решение задачи Коши для обыкновенного дифференциального уравнения (ОДУ) 1 порядка и оценить погрешность решения задачи:

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Задать исходные данные: функцию f правой части, начальное значение y₀
2. Используя функцию eyler, найти приближенное решение задачи Коши с шагом h=0.1 по явному методу Эйлера.
3. Используя встроенную функцию rkfixed пакета MathCAD, найти приближенное решение задачи Коши с шагом h=0.1 по методу Рунге-Кутты 4 порядка точности.
4. Найти решение задачи Коши аналитически.
5. Построить таблицы значений приближенных и точного решений. На одном чертеже построить графики приближенных и точного решений.
6. Оценить погрешность приближенных решений двумя способами:
   a) формуле =max(y(t_i)-y_i), где y(t_i) и y_i - значения точного и приближённого решений в узлах сетки t_i, i=1,...,N.
   b) по правилу Рунге (по правилу двойного пересчета).
7. Выяснить, при каком значении шага h = h* решение, полученное по методу Эйлера, будет иметь такую же погрешность (см. п. 6а), как решение, полученное с помощью метода Рунге-Кутты с шагом h=0.1.

Необходимый теоретический материал

Постановка задачи. Классификация приближенных методов.

Будем рассматривать обыкновенное дифференциальное уравнение (сокращенно ОДУ) первого порядка

y'(x)=f(x,y), x [x0,b]

(1.1)

с начальным условием

где f(x,y) - некоторая заданная, в общем случае, нелинейная функция двух переменных.
Будем считать, что для данной задачи (1.1)-(1.2), называемой начальной задачей или задачей Коши, выполняются требования, обеспечивающие существование и единственность на отрезке [x₀,b] ее решения y=y(x).
Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнение интегрируется в квадратурах. В приложениях крайне редко встречаются уравнения, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.
Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и "законного" применения того или иного метода.
Несмотря на внешнюю простоту уравнения (1.1), решить его аналитически, т.е. найти общее решение y = y(x,C) с тем, чтобы затем выделить из него интегральную кривую y = y(x), проходящую через заданную точку (x₀,y₀), удается лишь для некоторых специальных типов таких уравнений. Поэтому, как и в родственной для (1.1) - (1.2) задаче вычисления интегралов, приходится делать ставку на приближенные способы решения начальных задач для ОДУ.

Приближённые методы можно разделить на три группы:

1. приближенно-аналитические методы;
2. графические или машинно-графические методы;
3. численные методы.

Наиболее значимыми в настоящее время, характеризуемое бурным развитием и проникновением во все сферы человеческой деятельности цифровой вычислительной техники, являются численные методы решения дифференциальных уравнений, предпологающие получение числовой таблицы приближенных значений y_i искомого решения y(x) на некоторой сетке x_i 0 [x₀,b] значений аргумента x. Что делать с получаемыми численными значениями решения, зависит от прикладной постановки задачи. Если речь идет о нахождении только значения y(b), тогда точка b включается как конечная в систему расчетных точек x_i, и все приближенные значения y_i=y(x_i), кроме последнего, учавствуют лишь как промежуточные, т.е. не требуют ни запоминания, ни обработки. Если же нужно иметь приближенное решение y(x) в любой точке x, то для этого к получаемой числовой таблице значений y_i можно применить какой либо из способов аппроксимации табличных функций, например, интерполяцию или сплайн- интерполяцию. Возможны и другие использования численных данных о решении.

Метод Эйлера. Геометрическая интерпретация метода Эйлера.

Учитывая ключевую позицию, которую занимает метод Эйлера в теории численных методов ОДУ, рассмотрим несколько способов его вывода. При этом будем считать, что вычисления производятся с расчетным шагом h = (b-x₀) / n, расчетными точками (узлами) служат точки x_i=x₀+i*h (i=0,1,...,n) промежутка [x₀,b] и целью является построение таблицы приближенных значений y_i решения y = y(x) задачи (1.1) - (1.2) в расчетных точках x_i.

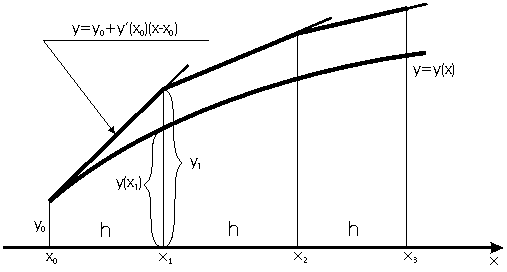
Пользуясь тем, что в точке x₀ известно и значение решения y(x₀)=y₀ (согласно(1.2)), и значение его производной y'(x₀)=f(x₀,y₀) (согласно(1.1)), можно записать уравнение касательной к графику искомой функции y=y(x) в точке (x₀;y₀):

При достаточно малом шаге h ордината

этой касательной, полученная подстановкой в правую часть (1.3) значения x₁=x₀+h, по непрерывности должна мало отличаться от ординаты y(x₁) решения y(x) задачи (1.1) - (1.2). следовательно, точка (x₁,y₁) пересечения касательной (1.3) с прямой x=x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую

y=y₁+f(x₁,y₁)(x-x₁),

которая уже приближенно отражает поведение касательной к y=y(x) в точке (x₁;y(x₁)). Подставляя сюда x=x₂(=x₁+h), иначе, пересекая эту "касательную" прямой x=x₂, получим приближение значения y(x₂) значением

y₂=y₁+hf(x₁,y₁)

и т.д. В итоге этого процесс, определяемого формулой

и называемого методом Эйлера, график решения y=y(x) данной задачи Коши (1.1)-(1.2) приближенно представляется ломаной, состовленой из отрезков приближенных касательных, откуда происходит другое название метода (1.5) - метод ломаных.

Методом Рунге-Кутты четвертого порядка точности называют одношаговый метод, относящийся к широкому классу методов Рунге-Кутты. В этом методе величины y_i+1 вычисляются по следующим формулам:

Оценка погрешности по правилу Рунге.

Практически оценить погрешность численного метода позволяет правило Рунге. Сначала вычисляют приближенное решение с шагом h, затем - с шагом h/2. Тогда для метода Рунге-Кутты 4 порядка точности справедливо приближенное равенство:

здесь - приближенное решение, вычисленное с шагом h, - приближенное решение, вычисленное с шагом h/2. За оценку погрешности решения, вычисленного с шагом h/2, принимают величину .

Решение:

Необходимые данные:

Определим правую часть уравнения:

Отрезок интегрирования:

Начальное значение в начале отрезка:

Шаг сетки:

Число узлов сетки:

Аналитическое решение исходного дифференциального уравнения:

Решение однородного уравнения:

Для нахождения значений возьмём интегралы от обеих частей уравнения:

По методу вариации произвольной постоянной заменим постоянную С на функцию C(t) и решим неоднородное уравнение:

Так как значение функции y уже известно, найдём значение производной и подставим в начальное уравнение:

Найдём значение C(t) путём интегрирования:

Подставим найденное значение в выражение для y:

Значение константы С отыщем из начальных условий: y0=2/3, x0=0

Подставим значение в у:

или, представляя как функцию:

Дискретизируем функцию s(t) на указанном отрезке интегрирования:

Обозначим функцию eyler, реализующую метод Эйлера:

Решим исходное уравнение с помощью описанной функции Эйлера:

Решим исходное уравнение, с помощью метода Рунге-Кутты:

Решения, полученные различными способами:

Аналитическим способом:	Методом Рунге-Кутты:	Методом Эйлера:

Построим графики решений ОДУ. По графикам видно, что решения, полученные методом Рунге-Кутты почти не отличаются от решений, полученных аналитическим путём. Можно сделать вывод о том, что метод Рунге-Кутты обладает большой точностью. Метод Эйлера, или метод касательных, не столь точен - отличия полученных значений от точных хорошо видны.

Рассчитаем погрешность полученных приближенных решений:

Погрешность метода Эйлера:	Погрешность метода Рунге-Кутты оценим по правилу Рунге:
	- порядок метода
	- уменьшенный вдвое шаг

Погрешность решения задачи методом Эйлера:

методом Рунге-Кутты:

Выясним, при каком значении шага h = h* решение, полученное по методу Эйлера, будет иметь такую же погрешность, как решение, полученное с помощью метода Рунге-Кутты с шагом h = 0.1 .

- шаг метода Эйлера

- число узлов сетки для метода Эйлера

- вектор значений функции, полученной аналитическим путем, в узлах сетки

- вектор значений функции, полученной аналитическим путем, в узлах сетки

Рассчитаем значения погрешностей вычисления для каждого узла сетки:

Вычисления показыают, что значительное (в несколько сотен раз) уменьшение шага сетки для решения по методу Эйлера не приводят к такой точности, которая достигнута решением уравнения методом Рунге-Кутты 4-го порядка точности. Проведённые выше вычисления показывают, что при уменьшении шага интегрирования в 256 раз, метода Эйлера даёт погрешность на 3 порядка больше, чем метод Рунге-Кутты.

Вывод: явный метод Эйлера - это численный метод 1-го порядка точности. Метод Рунге-Кутты - это метод 4-го порядка точности. Поэтому погрешности методов сильно (на несколько порядков) отличаются. В рассмотренном выше примере методом Рунге-Кутты было получено решение, которое незначительно отличается от решения, полученного аналитическим путём.