Задача 5. Построить кривую, приведя её уравнение к каноническому виду ортогональным преобразованием.

> По условию задачи:

> restart:with(plots):with(plottools):with(linalg):with(LinearAlgebra):

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the assigned name GramSchmidt now has a global binding

> f(x,y):=8*x^2+6*x*y=9;

Cоcтавим квадратичную форму и оценим её определитель:

> A := convert(hessian(op(1,f(x,y)/2),[x,y]),Matrix);
'det(A)'=det(A);
if (det(A)>0) then print (`Данная кривая имеет эллептический вид.`);
elif (det(A)<0) then print (`Данная кривая имеет гиперболический вид.`);
else print (`Данная кривая имеет параболичсекий вид.`);
end if;

Найдём собственные числа, решая характерестическое уравнение:

> (l,OwnMatrix):=Eigenvectors(A);

> 'det'('A'-lambda*E)=0;
charmat(-A,-lambda)=0;
sort(charpoly(-A,-lambda))=0;
'lambda'=convert(l,vector);

Найдём собственные вектора, решая характерестическое уравнение:

> for i to vectdim((convert(l,matrix))) do
lambda[i]=l[i];
charmat(-A,-l[i]);
print(`Собственный и нормализованый вектор:`);
'a'[i]=convert(col(OwnMatrix,i),matrix),
'e'[i]=convert(normalize(col(OwnMatrix,i)),matrix);od;

Выразим координаты старого базиса через коордиинаты нового:

> normM:=transpose(matrix(2,2,[normalize(col(OwnMatrix,1)),normalize(col(OwnMatrix,2))])):
xy:=matrix(2,1,[`x`,`y`]):x1y1:=matrix(2,1,[`x'`,`y'`]):
evalm(xy)=evalm(normM)*evalm(x1y1);
evalm(xy)=multiply(normM,x1y1);
x=(multiply(normM,x1y1))[1,1];y=(multiply(normM,x1y1))[2,1];

Подставим их в исходное уравниение и получим каноническое уравнение кривой в координатах нового базиса:

> subs(x=(multiply(normM,x1y1))[1,1],y=(multiply(normM,x1y1))[2,1],f(x,y));
expand(%);
%/(op(2,%));
f(`x'`,`y'`):=%:

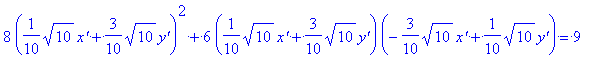
Выразим координаты в новом базисе через координаты в старом:

> solve({x=(multiply(normM,x1y1))[1,1],y=(multiply(normM,x1y1))[2,1]},{`x'`,`y'`});

Построим график данной кривой в системе координат XOY:

> coordp := [[-1,3],[1,3],[1,-3],[-1,-3],[-1,3]]:
rect1:=curve(coordp,linestyle=3):
c1:=col(OwnMatrix,1):
c2:=col(OwnMatrix,2):
X1Y1:=implicitplot({c1[1]*y=c1[2]*x,
c2[1]*y=c2[2]*x},
x=-6..6, y=-6..6,scaling=constrained,color=black,linestyle=DASH):
XY:=implicitplot({f(x,y)},
x=-6..6,y=-6..6,thickness=3,numpoints=600,labels=["",""]):
t1:=textplot([[c1[1]*2+.2,c1[2]*2, `x'`],
[-c2[1]*2, -c2[2]*2+.2,`y'`]],align={ABOVE,RIGHT},color=BLUE):
t2:=textplot([[6,.3,`x`],[-.7,6,`y`]],align={ABOVE,RIGHT},color=BLUE):
alpha:=arctan(1/3):rect2:=rotate(rect1,alpha):
plots[display]([XY,X1Y1,t1,t2,rect2],color=black,title="рис. 1");