Вернуться
на страницу <Model Vision Studium>
В начало
Приложение
Задание
Студент должен в качестве решения задачи
представить следующие результаты:
- описание системы, представленной в задаче, в
терминах унифицированного языка моделирования
UML;
- модель данной системы, реализованную в
подсистеме Simulink пакета Matlab на основе полученного
описания;
- модель данной системы, реализованную в пакете
Model Vision Studium на основе полученного описания;
- результаты, полученные в процессе исследования
данных моделей и их объяснение в терминах данной
прикладной области.
Примечание:
При построении модели любой из задач в пакете
Model Vision Studium необходимо реализовать трехмерную
анимацию (задача №1-10) или создать панель
управления параметрами, содержащую в себе
компоненты двухмерной анимации (задача №11, №12).
Задача 1 | Задача
2 | Задача 3 | Задача
4 | Задача 5 | Задача
6
Задача 7 | Задача 8
| Задача 9 | Задача
10 | Задача 11 | Задача
12
Задача №1
Переменная сила Q, изменяющаяся по
гармоническому закону (1) или (2), передается на
фундамент машиной с неуравновешенным ротором
(рис.1):
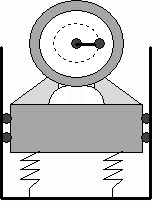
Рисунок 1
Q1 = H1*Sin(w1*t) (1)
Q2 = H2*Cos(w2*t) (2)
где
H1 и H2 - амплитуда
возмущающей силы,
w1 и w2 - частота возмущающей
силы.
Пусть H1 = 2см, H2 = 3см, w1
= 0.3с-1, w2 = 0.5с-1.
Гармонические законы сменяют друг друга с
периодом в 50 секунд.
Пусть k = 0.4с-1 - это собственная частота
рассматриваемой системы. Если она не совпадает с
частотой возмущающей силы, в данный момент
времени предаваемой на фундамент (то есть k № w1
или k № w2), то значение координаты q,
по оси которой будут происходить колебания,
определяются следующими уравнениями:
для гармонического закона (1):
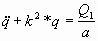 (3) (3)
для гармонического закона (2):
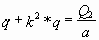 (4) (4)
где
а = 1 с-2 - инерционный коэффициент.
Начальные условия:
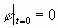 (5) (5)
Если собственная частота системы совпадает с
частотой возмущающей силы, в данный момент
времени предаваемой на фундамент (то есть k = w1
или k = w2), то во избежание резонанса
воздействие на фундамент прекращается, значение
частоты, передаваемой на фундамент на момент
возникновения резонанса уменьшается на 10% и
через 1 секунду колебания возобновляются по тому
же закону, что действовал до пререрыва уже с
новой частотой.
Построить модель данной системы и модель для
двух таких машин работающих одновременно и
независимо друг от друга. Вторая машина обладает
аналогичным поведением, за исключением того, что
переменная сила Q’ для нее задается теми же
законами, но с иными параметрами:
Q1‘ = H3*Sin(w3*t) (1’)
Q2‘ = H4*Cos(w4*t) (2’)
где
H3 и H4 - амплитуда
возмущающей силы,
w3 и w4 - частота возмущающей
силы.
Задача №2
Дана система из двух маятников - маятника 1
и обращенного маятника 2 (рис.2):
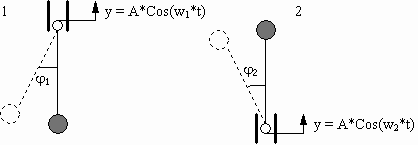
Рисунок 2
Точка подвеса первого маятника гармонически
колеблется по вертикали около среднего
положения по закону (1), а точка подвеса второго
маятника гармонически колеблется по вертикали
около среднего положения по закону (2):
y1 = A*Cos(w1*t) (1)
y2 = A*Cos(w2*t) (2)
где
А - амплитуда колебаний,
w1 и w2 - частоты колебаний.
Пусть A = 2м, w1 = 3с-1, w2 =
3с-1.
При этом каждые 10 секунд значение A
изменяется на величину ±0.5 поочередно.
Длина каждого из маятников равна l = 40м.
Пусть j1 - это угол отклонения первого
маятника от строго вертикального положения, а j2
- это угол отклонения второго маятника от строго
вертикального положения.
У первого маятника j1 изменяется в
соответствии с уравнением:
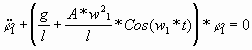 (3) (3)
У второго маятника поведение иное: если 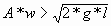 , где g - это ускорение
свободного падения, то маятник находится в
устойчивом состоянии и j2 = 0. , где g - это ускорение
свободного падения, то маятник находится в
устойчивом состоянии и j2 = 0.
В противном случае, j2 изменяется в
соответствии с уравнением:
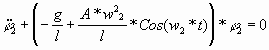 (4) (4)
У обоих маятников в начальный момент времени
отклонение от положения равновесия составляет 0,1
градуса. Значения j1 и j2
изменяются в пределах от 0 до 360 градусов.
Построить модель данной системы.
Задача №3
Дан неровный участок со сложным профилем. По
нему движутся две идентичные системы, каждая из
которых представляет собой подрессорный груз
массой m = 0,7кг, прикрепленный к безотрывно
движущемуся с постоянной горизонтальной
скоростью V1 = 0,9м/с (для первой системы) и
V2 = 1м/с (для второй системы) колесу
(рис.3):
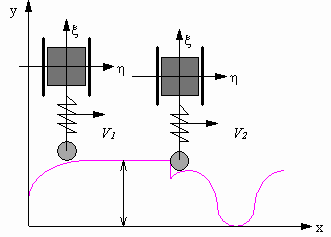
Рисунок 3
Профиль участка имеет следующий вид:
известно, что при скорости V1 система
движется в течении отрезка времени Time1 =
20с по участку, описываемому уравнением (1), а
делее с периодичностью Time2 = 30с для
скорости V1 (Time2’ = 27с для
скорости V2) профиль участка
описывается уравнениями (2) и (3) поочередно:
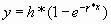 (1) (1)
y = A1*Cos x (2)
y = A2*Sin x (3)
где
h - предел, к которому стремится высота
неровности,
g - параметр, характеризующий кривизну
профиля,
А1 и А2 - амплитуды колебаний.
Пусть h = 1м, g = 1, А1 = 0,8м, А2 = 0,7м.
Первая система в начальный момент времени
расположена в начале пути, а вторая расположена в
начале косинусоидального участка. В начальный
момент времени начинает двигаться первая
система со скоростью V = V1, а вторая
остается на месте. Как только первая система
достигает конца экспоненциального участка,
начинает свое движение вторая система со
скоростью V = V2 (где V2 > V1),
и далее обе системы движутся вместе.
Так как x = V*t (где V = V1),
дифференциальные уравнения, описывающие
вертикальные колебания x (в начальный момент
времени отвутствующие) первого груза
записываются следующим образом:
для уравнения (1):
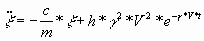 (4) (4)
для уравнения (2):
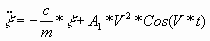 (5) (5)
для уравнения (3):
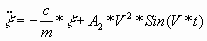 (6) (6)
где
с - жесткость упругой подвески.
Пусть с = 0,5кг/с2.
Движения второго груза описывается
уравнениями (5) и (6) при условии, что V = V2.
Если предел h меньше hmin = 0,001м или
амплитуды А1 и А2 меньше Аmin
= 0,01м, то профиль участка считается
прямолинейным и колебания грузов описываются
уравнением:
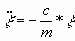 (7) (7)
Построить модель данной системы.
Задача №4
Жесткая плоская пластинка длиной l = 5м
находится в потоке газа (жидкости), скорость V =
1м/с которого направлена вдоль срединной
плоскости пластинки в невозмущенном состоянии
равновесия (рис.4):
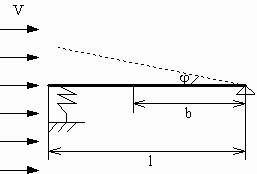
Рисунок 4
В этом положении аэродинамические силы равны
нулю и пластинка находится в равновесии под
действием силы тяжести и реакции опор. При
отклонении пластинки возникают
аэродинамические давления, зависящие от угла
отклонения пластинки j. В начальный момент
пластинка отклоняется от положения равновесия
на угол 0.01 градуса.
Пусть I = 1кг*м2 - момент инерции
пластинки относительно оси шарнира; тогда
дифференциальным уравнением движения будет:
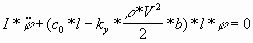 (1) (1)
где
c0 - коэффициент жесткости пружины,
Ky - постоянный аэродинамический
коэффициент,
r - плотность газа,
b - расстояние от оси шарнира, определяющее
точку приложения равнодействующих
аэродинамических давлений на пластину.
Пусть c0 = 0,5кг/с2, Ky = 0,5м*с2,
r = 2кг/м3, b = 1м.
Уравнение (1) выполняется при условии 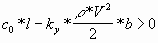 . В противном случае, под
действием аэродинамических сил пластинка снова
возвращается в положение равновесия. . В противном случае, под
действием аэродинамических сил пластинка снова
возвращается в положение равновесия.
Каждые 5 секунд скорость подаваемого газа то
увеличивается на 50%, то возвращается к прежнему
значению. Также каждые 10 секунд плотность газа то
увеличивается на 50%, то возвращается к прежнему
значению.
Построить модель данной системы, а также модель
системы, состоящей из двух систем типа
"пластинка в потоке газа", несвязанных друг
с другом. Вторая система "пластинка в потоке
газа" идентична первой, за исключением того,
что в ней пластинка имеет другую длину l1
> l, а поток газа имеет другую скорость V1>V
и иную плотность r1 < r.
Задача №5
Дана система из двух тел с массами m1
и m2, соединенных двумя пружинами,
жесткости которых равны c1 и с2
(рис.5):
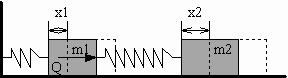
Рисунок 5
Пусть m1 = 1кг, m2 = 1кг, c1
= 1кг/с2, с2 = 1кг/с2.
На левый груз системы действует гармоническая
возмущающая сила Q, задаваемая с интервалом в
20 секунд то законом (1), то законом (2):
Q = H1*Sin(w*t) (1)
Q = H2*Cos(w*t) (2)
где
H1 и H2 - амплитуды колебаний,
w - частота колебаний.
Пусть H1 = 1м, H2 = 1,5м, w = 2с-1.
Частота колебаний вне зависимости от закона
колебаний каждые 25 секунд то уменьшается на 50%, то
возвращается к прежнему значению.
Пусть x1 и x2 - горизонтальное
отклонение грузов от положения равновесия (в
начальный момент времени отсутствующее). Тогда
уравнениями движения будут:
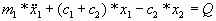 (3) (3)
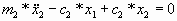 (4) (4)
Построить модель данной системы, а также модель
системы, состоящей из двух систем типа "два
груза", несвязанных друг с другом. Вторая
система "два груза" идентична первой, за
исключением того, что в ней левый груз имеет
другую массу m2< m’1 < m1, а
правая пружина имеет другую жестксть с’2>
с2.
Задача №6
Дан вертикальный безмассовый упругий
стержень длиной l = 5м с постоянной жесткостью
сечения EJ = 1кг*м3/с2. С концом
стержня связан сосредоточенный груз массой m =
1кг. Верхней опорой стержня служит неподвижный
шарнир, а нижней опорой служит подвижная втулка с
шарикоподшибником (рис.6):
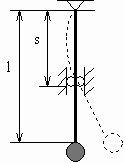
Рисунок 6
Расстояние между опорами s < l не
постоянно и изменяется засчет движения втулки
попеременно с периодом 30 секунд по одному из двух
гармонических законов:
s = H1*Cos(w1*t) (1)
s = H2*Sin(w1*t) (2)
где
H1 и H2 - амплитуды колебаний,
w1 - частота колебаний.
Пусть H1 = 1,5м, H2 = 2м, w = 1с-1.
Частота колебаний вне зависимости от закона
колебаний каждые 20 секунд то уменьшается на 40%, то
возвращается к прежнему значению.
Состоянию равновесия соответствует положение
груза на вертикали и прямолинейная форма оси
стержня. При возмущении этого состояния груз
отклоняется в сторону, ось балки изгибается, и
последующее движение описывается
дифференциальным уравнением:
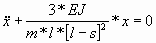 (3) (3)
В начальный момент времени происходит
отклонение груза на расстояние x0 = 0,1м.
Если x превышает пороговое значение xmax
= 3м, то стержень разрушается.
Построить модель данной системы и модель для
двух таких систем, работающих одновременно и
независимо друг от друга. Вторая система
обладает аналогичным поведением, за исключением
того, что переменная сила s’ для нее задается
теми же законами, но с иными параметрами:
s’ = H3*Cos(w2*t) (1)
s’ = H4*Sin(w2*t) (2)
где
H3 и H4 - амплитуды колебаний,
w2 - частота колебаний.
Задача №7
Дана система из груза массой M = 1кг,
связанного с безмассовой жесткой упруго
закрепленной балкой.
Пусть 2l - длина балки, с0 -
коэффициент жесткости пружины. Один конец балки
закреплен на шарнире, расположенном на
неподвижной опоре (рис.7):
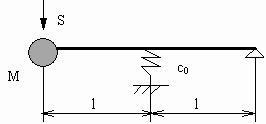
Рисунок 7
Пусть l = 1м, с0 = 1кг/с2.
В начальный момент времени происходит
однократный вертикальный удар по грузу с
величиной мгновенного ударного импульса S = 2Н*с.
Скорость груза получает мгновенное приращение,
из чего следуют начальные условия:
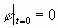 (1) (1)
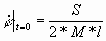 (2) (2)
где
j - это угол отклонения системы от положения
равновесия.
Движение системы описывается следующим
уравнением:
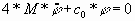 (3) (3)
Через 25 секунд после начала колебаний масса
груза M мгновенно уменьшается на 50%. Далее
движение системы продолжается, но уже с грузом
новой массы.
Если угол j становиться больше предельного
значения 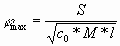 , то
происходит разрушение системы. , то
происходит разрушение системы.
Построить модель системы "балка - груз", а
также модель системы, состоящей из двух систем
"балка - груз", несвязанных друг с другом.
Вторая балка с грузом идентична первой, за
исключением того, что удар по грузу в ней
происходит через 10 секунд после того, как
произошел удар по грузу в первой системе
"балка - груз".
Задача №8
В воде плавает кусок пробки в виде
параллелепипеда с площадью основания S = 1 м2
и высотой H = 0,5 м. Пробку погружают в воду на
небольшую глубину x0 = 5 см и отпускают
(рис.8):
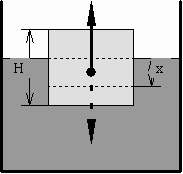
Рисунок 8
В результате пробка начинает совершать
колебания. Сопротивление воды не учитывается.
Изменение глубины погружения пробки в воду х
описывается следующим уравнением:
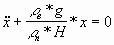 (1) (1)
с начальными условиями:
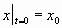 (2) (2)
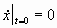 (3) (3)
где
rв = 1000 кг/м3 - плотность воды,
rп = 200 кг/м3 - плотность пробки,
g - ускорение свободного падения.
Пусть существует вторая точно такая же система
"вода - пробка" в которой пробку в начальный
момент времени не погрузили в воду и отпустили, а
сообщили ей скорость, равную v0 = 1м/с.
Пусть в данной системе существует сила
сопротивления воды, пропорциональная скорости
пробки: Fc = -r*v, где r = 1кг/с -
коэффициент пропорциональности. Колебания в
этой системе описываются уравнением:
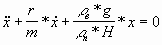 (4) (4)
с начальными условиями:
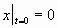 (5) (5)
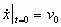 (6) (6)
где
m - масса пробки.
Построить модель системы, состоящей из этих
двух систем "вода - пробка", несвязанных друг
с другом. Построить также модель системы, в
которой каждые 20 секунд в первой системе вода
мгновенно "превращается" в ртуть ( а ртуть с
той же периодичностью - в воду), а во второй
системе каждые 25 секунд происходят аналогичные
"превращения" воды в спирт. Плотность ртути -
rр = 1360 кг/м3, плотность спирта - rс
= 790 кг/м3.
Задача №9
Материальная точка массы m = 1 кг находится
в поле тяготения тонкого кольца массы M = 1020
кг и радиуса R = 1 км. В начальный момент
времени точка помещается в точку Q1,
расположенную на оси кольца на расстоянии x0
< R от плоскости кольца и начинает совершать
колебательные движения (рис.9):
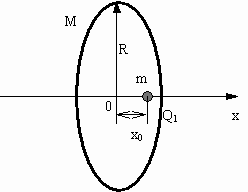
Рисунок 9
Если x0 < 0.1*R, то колебания x
описываются следующим уравнением:
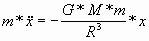 (1) (1)
Если x0 і 0.1*R или в результате
колебаний выполняется условие x і 0.1*R, то
колебания описываются следующим уравнением:
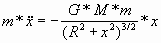 (2) (2)
где
G - гравитационная постоянная.
Пусть x0 = 1м.
Каждые 15 секунд радиус кольца поочередно
мгновенно расширяется и сжимается в 10 раз. Если
точка отклоняется от кольца на расстояние,
превышающее в 10 раз его первоначальный радиус,
система разрушается.
Построить модель данной системы, а также модель
системы, состоящей из двух систем
"материальная точка - кольцо", несвязанных
друг с другом. Вторая система "материальная
точка - кольцо" идентична первой, за
исключением того, что в ней радиус кольца
изменяется в 5 раз каждые 20 секунд.
Задача №10
В длинной вертикальной цилиндрической
трубке, закрытой с нижнего конца, может ходить
без трения поршень, масса М =10кг которого
велика по сравнению с массой идеального газа,
заключенного внутри трубки. В положении
равновесия расстояние между поршнем и дном
трубки равно l0 = 1000м (рис.10):
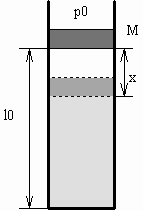
Рисунок 10
Площадь поперечного сечения трубки равна S =
1м2, на поршень действует нормальное
атмосферное давление p0. В начальноый
момент времени поршень отклоняют от положения
равновесия на расстояние x << l0. В
результате этого поршень начинает совершать
колебания, описываемые следующими уравнениями:
если p0 № 0:
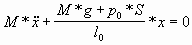 (1) (1)
если p0 = 0:
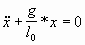 (2) (2)
где
g - ускорение свободного падения.
Пусть x = 1м.
Атмосферное давление каждые 10 секунд
мгновенно изменяет свое значение с нормального
значения на меньшее на 80% (и обратно).
Построить модель данной системы, а также модель
системы, состоящей из двух систем типа "трубка
с поршнем", несвязанных друг с другом. Вторая
"трубка с поршнем" идентична первой, за
исключением того, что в ней поршень имеет другую
массу М’ > M и другую площадь поперечного
сечения трубки S’>S.
Задача №11
Дана однокамерная фармакокинетическая
модель с всасыванием (рис.11):
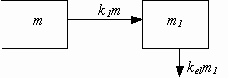
Рисунок 11
где
1 - это место введения лекарственного
препарата,
2 - камера.
Камера представляет собой ограниченный в
пространстве объем жидкости (ткани), неизменный с
течением времени. Дан определенный объем
лекарственного препарата, который всасывается в
камеру пропорционально своей массе в
соответствии с уравнением:
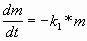 (1) (1)
где
m - масса лекарственного препарата в месте
введения 1,
k1 - константа скорости поступления
препарата в камеру (константа скорости
всасывания).
Пусть k1 =0,3 с-1 .
Предполагается, что масса лекарственного
препарата в 1 в начальный момент времени
равна М = 30мг, причем в самой камере в
начальный момент времени препарата нет. Тогда
масса лекарственного препарата в камере
изменяется в соответствии с следующим
уравнением:
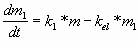 (2) (2)
где
m1 - масса лекарственного препарата в
камере,
kel - константа элиминации (выведения)
лекарственного препарата из камеры.
Пусть kel =0,5 с-1 .
Как только масса лекарственного препарата в
месте введения становится меньше порогового
значения e = 0,001мг, засекается отрезок времени Time
= 10с, по истечении которого в месте введения
уничтожаются все остатки прежней дозы препарата
и вводится новая доза m = M.
Существует более сложная система, называемая
двухкамерной фармакокинетичкской моделью с
всасыванием (рис. 12):
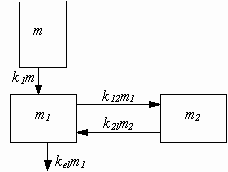
Рисунок 12
В ней лекарственный препарат вводится из
аналогичного ранее описанному места введения 1’
и выводится из камеры 2’, но существует еще
камера 3, подсоединенная к камере 2’.Между
камерами 2’ и 3 может циркулировать
лекарственный препарат.
В этой модели масса лекарственного препарата в
месте введения описывается также уравнением (1) с
теми же начальными условиями. Массы же в камерах 2’
и 3 описываюстя уравнениями (3) и (4)
соответственно:
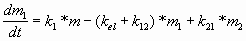 (3) (3)
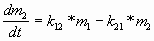 (4) (4)
где
m2 - масса лекарственного препарата в
камере 3,
k12 - константа скорости поступления
препарата из камеры 2’ в камеру 3.
k21 - константа выведения лекарственного
препарата из камеры 3 в камеру 2’.
Пусть k12 =0,4 с-1, k21 =0,6 с-1.
Как и в первой системе, в начальный момент
времени в камерах 2’ и 3 лекарственный
препарат отсутствует. Как и в первой системе, как
только масса лекарственного препарата в месте
введения становится меньше порогового значения e’,
засекается отрезок времени Time1, по
истечении которого в месте введения
уничтожаются все остатки прежней дозы препарата
и вводится новая доза m = M.
Построить модель системы, содержащей обе
фармакокинетические модели, несвязанные друг с
другом с различными местами введения
лекарственного препарата. Также построить
модель системы, состоящей из обеих
фармакокинетических моделей, имеющих общее
место введения препарата. Скорость всасывания
лекарственного препарата k1 в обеих
фармакокинетических моделях одинаковая, отрезок
времени Time’ и пороговое значение e’ для
места введения препарата совпадают со
значениями, принятыми для однокамерной
фармакокинетической модели с всасыванием.
Задача №12
Даны две биологические популяции,
оспаривающие одну и ту же пищу. Пусть это будут
популяции медведей (численностью N1) и
волков (численностью N2) (рис.13):
Рисунок 13
Пусть при количестве пищи, достаточном для
полного удовлетворения рассматриваемых видов,
существуют постоянные положительные
коэффициенты прироста популяций: e1 = 0,7мес-1
для медведей и e2 = 0,9мес-1 для
волков. Для каждого вида заданы "коэффициенты
прожорливости" - g1 = 0,7кг-1 и g2
= 0,5 кг-1, соответствующие потребности в
пище для каждой из двух популяций.
Пусть F(N1, N2) - количество пищи,
поедаемой обеими популяциями в единицу времени.
Оно задается уравнениями (1) и (2), где уравнение (1)
соответствует случаю, когда обе популяции
активны, а уравнение (2) - когда медведи впадают в
спячку. Переключение между режимами (1) и (2)
происходит периодически, причем с режима (1) на
режим (2) переключение происходит через отрезок
времени Time1 = 9мес, а с режима (2) на режим
(1) - через Time2 = 3мес:
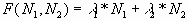 (1) (1)
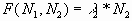 (2) (2)
где
l1 и l2 - некие положительные
коэффициенты.
Пусть l1 = 0,01кг/(мес*шт), l2 =
0,02кг/(мес*шт).
В начальный момент времени популяции
обладают начальной численностью N1’ =
10шт и N2’= 20шт.
Тогда развитие популяций описывается
следующими уравнениями:
медведи:
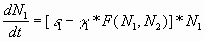 (3) (3)
волки:
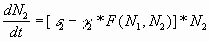 (4) (4)
Как только численность той или другой
популяции становится меньше 1 (умирает последняя
особь), засекается отрезок времени Time3 =
3мес (если это медведи) или Time3’ = 5мес
(если это волки), по истечении которого вместо
прежней популяции поселяется новая популяция с
новой начальной численностью (N1’ если
это медведи и N2’ если волки).
Построить модель данной системы, а также модель
системы, состоящей из двух систем типа "две
популяции", несвязанных друг с другом. Вторая
система "две популяции" идентична первой, за
исключением того, что в ней вместо медведей и
волков в качестве конкурирующих видов
рассматриваются лоси и олени, имеющие иные
значения коэффициентов прироста e1’и e2’,
другие значения "коэффициентов
прожорливости" g1’ и g2’,а
также иные значения коэффициентов l1 и
l2.
В начало
Вернуться на страницу <Model Vision
Studium> |

