Использование интегрированной символьной системы Mathematica при изучении курса высшей математики в вузе

АВТОРЕФЕРАТ диссертации
Дьяченко С.А.

В начало

Основное содержание работы

• Введение
• Первая глава “Теоретические основы использования новых компьютерных технологий в процессе обучения высшей математике в вузе”
• Вторая глава “Методические основы применения ИССМ при обучении курсу высшей математики в вузе”
• Педагогический эксперимент

Во введении обосновывается актуальность темы исследования, определяется объект, предмет, цель, гипотеза и задачи исследования, указывается новизна, теоретическая и практическая значимость работы, положения, выносимые на защиту.

Первая глава “Теоретические основы использования новых компьютерных технологий в процессе обучения высшей математике в вузе” состоит из трех параграфов.

В первом параграфе проанализировано современное состояние проблемы использования новых компьютерных технологий в вузе.

В современных условиях будущий специалист сталкивается с необходимостью восприятия и переработки информации, передаваемой по каналам средств массовой информации, в том числе и с использованием компьютерной техники. Сформированное в настоящее время новое специфическое направление в педагогической науке – медиаобразование призванно помочь студентам и школьникам лучше адаптироваться в мире медиакультуры, освоить язык средств массовой информации, научиться анализировать медиатексты и т. д. Его основная задача – подготовить новое поколение к жизни в современных информационных условиях, предполагающих восприятие и понимание различной информации, овладение способами общения на основе невербальных форм коммуникации.

Использование компьютерных технологий в образовании можно рассмотреть как часть медиаобразования, и определить компьютерные технологии как совокупность приемов и методов, направленных на получение, переработку и хранение информации средствами компьютерной техники.

Анализ трудов известных педагогов и психологов, а также анкетирование преподавателей вузов позволили обобщить достоинства и трудности применения компьютерных технологий в процессе обучения в вузе; сформулировать основное требование к будущему специалисту – постижение общих методов, познание существенного, умение ориентироваться в поисках информации. Это привело к необходимости разработки научных основ применения новых информационных технологий в процессе обучения и создания конкретных методических рекомендаций по использованию компьютера при изучении курса высшей математики.

Во втором параграфе “Интегрированная символьная система Mathematica и ее дидактические возможности обучения высшей математике в вузе” рассмотрено одно из новых направлений в области проведения математических исследований – интегрированная символьная система Mathematica (ИССМ), созданная фирмой Wolfram Research Ltd. (США).

Наше исследование опирается на версию Mathematica 3, которая используется как калькулятор для проведения численных расчетов; для построения графиков функций одной или двух переменных, для вычерчивания кривых и изображения поверхностей по их уравнениям; как средство для представления математических сведений и т. д.

Дидактические возможности ИССМ позволяют рассмотреть интегрированную символьную систему Mathematica как метод обучения высшей математике, который мы рассматриваем как способ, средство или путь, при помощи которого учитель, вооружает обучаемых знаниями, развивает познавательную самостоятельность. Основную цель рассматриваемого метода мы видим в организации преподавателем на его основе такого процесса обучения, который обеспечивает активное усвоение студентами материала курса высшей математики и способствует формированию творческой познавательной самостоятельности, характеризующийся такими проявлениями как саморегуляция познавательной деятельности, синтез познавательного мотива и способов самостоятельного поведения, устойчивое положительное отношение обучаемых к познанию. При этом уровень познавательной самостоятельности должен определяется степенью дозировки помощи обучаемому в решении математических задач.

Для полной характеристики метода обучения на основе ИССМ была использована классификация, предложенная Ю. К. Бабанским позволившая отнести его к методам осуществления и организации учебно-познавательной деятельности студента. По источнику передачи и восприятия информации он относится к наглядным и практическим методам, поскольку позволяет иллюстрировать, демонстрировать изучаемые объекты и решать математические задачи. По логике передачи и восприятия учебной информации он классифицируется как дедуктивный метод, так как указывает общий способ решения задач определенного типа. По степени самостоятельности мышления обучаемых при овладении знаниями метод является поисковым и исследовательским. По степени управления учебной деятельностью метод направлен на активизацию самостоятельной деятельности студентов.

Использование метода обучения на основе ИССМ реализуются через включение системы лабораторных работ в процесс обучения и направлено на формирование обобщенных понятийных систем, приемов умственной деятельности на основе активизации познавательной самостоятельности. Этот метод в наибольшей степени соответствует одной из наиболее перспективных дидактических моделей, рассмотренных в современной педагогике, называемой знаковой моделью научения, описанной Н. В. Метельским, основной принцип построения которой – “Начинать обучение не с частного, а с общего, не с частей, а с целого”.

Таким образом, как показало наше исследование, ИССМ, являясь программным продуктом высокого качества, обладает большими дидактическими возможностями и может быть использована для повышения эффективности обучения высшей математике в вузе.

В третьем параграфе “Философские и психолого-педагогические основы использования ИССМ при изучении курса высшей математики” излагается построение процесса обучения базирующегося на современной концепции естествознания – концепции системного метода.

Системный метод позволяет рассмотреть диалектическое взаимодействие процесса обучения с использованием ИССМ с различными областями наук: математикой, информатикой, педагогикой, психологией, теорией и методикой преподавания математики.

Психолого-педагогические аспекты такого взаимодействия, по нашему мнению, базируются на личностно-ориентированном подходе в образовании, когда студент становится во главе процесса обучения, его активным субъектом, а преподаватель – компетентным консультантом и помощником, формирующим познавательную самостоятельность обучаемого. При этом традиционная парадигма образования “преподаватель – учебник – студент” заменяется новой парадигмой “студент – учебник – преподаватель”, отражающей гуманистические тенденции в педагогике и нарушающей главное условие традиционного образования – наличие готовых, систематизированных знаний, подлежащих усвоению.

Сведения могут представлять собой не только знания, но и информацию. Знания – проверенный практикой результат познания действительности, основная особенность которого – систематичность, непротиворечивость, объективность. Информация – сведения любого характера, иногда сомнительной достоверности. В их систематизации мы видим задачу самого обучающегося. Основным элементом учебного процесса становится не только знание, но и информация, а в качестве нового средства обучения выступает компьютер. В этих условиях с учетом информатизации образования возникает вопрос о взаимодействии традиционных и новых средств обучения.

Такой подход позволяет нам пересмотреть новую парадигму образования и прийти к ее усовершенствованной форме, при которой компьютер и учебник параллельно используются в учебном процессе (схема 1). Назовем эту парадигму – новой компьютерной парадигмой образования.

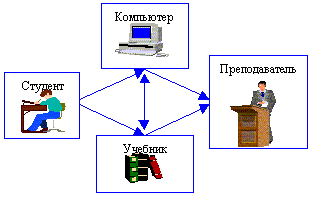
Схема 1

Преимущества такой парадигмы в том, что она успешно сочетает основное свойство учебника – доступность и основное свойство компьютера – высокое качество предъявления информации. Согласно ей студент обращается в поисках учебной информации либо к компьютеру, либо к учебнику по своему желанию, т. е. при работе на компьютере он может использовать учебник, а при чтении учебника обращаться к компьютерной информации. Имеющие навыки пользователя, высокий уровень знаний по основным предметам, по мнению К. А. Вольхина и И. Н. Вольхиной, используют компьютер в качестве основного средства обучения. При их отсутствии первоочередными средствами будут традиционные, а умения, связанные с применением компьютера студентам придется приобретать параллельно с изучением основного предмета.

Новая компьютерная парадигма образования с привлечением ИССМ ставит на качественно более высокий уровень весь процесс обучения, основными компонентами которого, согласно теории В. И. Крупича, являются содержание обучения, деятельность учения и деятельность преподавания. Содержание курса высшей математике выступает теперь в качестве одного из основных источников познания и стимулирования познавательного интереса. Деятельность учения получает направление на формирование умений приобретать новые знания и применять их в различных ситуациях. ИССМ поднимает познавательную самостоятельность студентов на творческий уровень. Возрастают требования к преподавателю, деятельность которого направлена не просто на контроль знаний и умений обучаемых, а на диагностику их деятельности, оказание своевременной помощи квалифицированными действиями, устранение намечающихся трудностей в познании и применении знаний.

Итак, анализ философских и психолого-педагогических основ использования ИССМ показал, что ее внедрение в качестве метода обучения способно качественно повысить все компоненты процесса обучения высшей математике в вузе. Это позволяет сделать вывод о необходимости создания учебно-методического комплекса.

Вторая глава “Методические основы применения ИССМ при обучении курсу высшей математики в вузе”.

В первом параграфе построена методическая модель обучения на основе ИССМ. Ее методологической и теоретической основой явились концепция системного метода, личностно-ориентированный подход к обучению, теоретические основы познавательной самостоятельности, знаковая модель научения, отвечающая методу обучения на основе ИССМ, а также содержание курса высшей математики в вузе, отвечающее государственному образовательному стандарту высшего профессионального образования.

Замысел построения модели отражает схема 2.

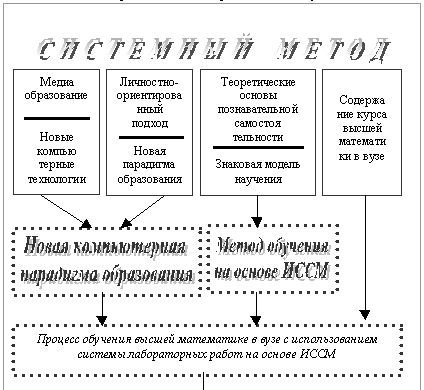
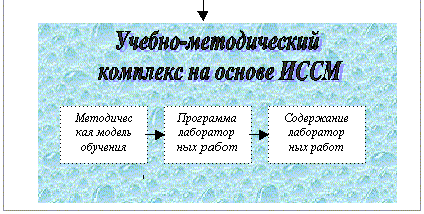
Схема 2

Системный метод требует рассмотрения в единстве содержательной и процессуальной сторон обучения, которые взаимосвязаны. Знания, полученные на лекциях, составляют теоретическую базу курса. Умения и навыки решения конкретных математических задач формируются на практических занятиях. Лабораторные работы являются связующим звеном теоретических знаний студента и его практических умений и навыков. С помощью ИССМ можно эффективно автоматизировать трудоемкие и опасные ошибками преобразования, иллюстрировать графические объекты и т. д.

Результат этого взаимодействия представлен на схеме 3.

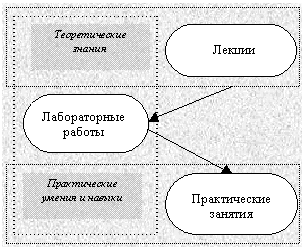
Схема 3

При этом с точки зрения системного метода лабораторные работы также должны составлять систему, т. е. уместно было бы говорить о системе лабораторных работ с использованием ИССМ как определенной целостности. При таком подходе учитываются все компоненты процесса обучения: целевой, содержательный, логический, гносеологический, управленческие аспекты деятельности, т. е. все наиболее известные ее компоненты, выделенные современной наукой, что обеспечивает системе лабораторных работ определенную целостность и дает возможность говорить о возникновении нового качества – о формировании умений и навыков использования новых информационных технологий для проведения математических исследований, и как следствия о повышении уровня знаний студентов, усиление их познавательной самостоятельности и т. д.

Для того чтобы система лабораторных работ с использованием ИССМ органично включалась в процесс обучения высшей математике в вузе нужно опираться на известные принципы дидактики: научности, доступности, наглядности, активного обучения, прочности, индивидуального подхода.

Для определения внутренней структуры каждой лабораторной работы мы требуем соблюдения дополнительных принципов: инвариантности, параллельности, содержательного повтора, нелимитируемости, однотипности, непрерывного повторения, сравнения, полноты. Их выполнение позволяет определить систему заданий для изучения каждой конкретной темы.

С учетом перечисленных принципов нами разработаны программа и содержание системы лабораторных работ по курсу высшей математики для студентов первого курса вузов естественно-технического профиля. Программа лабораторных работ представлена на таблице 1.

Курс лабораторных работ лучше начать с вводной части, в которой дать краткую историческую справку о возникновении символьных систем в нашей стране и за рубежом, рассказать о перспективах их развития.

Лабораторные работы охватывают основные разделы высшей математики: линейную и векторную алгебру, аналитическую геометрию, математический анализ и проводятся на первом курсе после того, как прослушан курс лекций по соответствующему разделу высшей математики. При этом имеется в виду, что первоначальные сведения о работе на компьютере студенты получают на первых занятиях по информатике.

Каждая работа состоит из теоретической и практической части. Теоретическая часть знакомит студентов со способами представления информации с помощью ИССМ, в практической части предлагается решение конкретных математических заданий. Основная задача системы лабораторных работ – помочь студентам точнее понять изучаемый математический материал, проиллюстрировать примерами общие формулы и отношения, установить взаимосвязь некоторых понятий, что достигается с помощью автоматизации преобразований, проверки, визуализации знаний, полученных на лекциях по соответствующей теме. К каждой лабораторной работе даны методические рекомендации, включающие рекомендуемые вопросы для повторения изучаемого материала.

Таблица 1

Педагогический эксперимент в рамках данного исследования проводился поэтапно на протяжении трех лет с 1998 по 2000 год в Орловском государственном аграрном университете и преследовал следующие цели: оценка эффективности методики системы лабораторных работ на основе ИССМ в курсе высшей математики, построенной на научно-теоретических положениях, разработанных автором; выявление влияния предложенного учебно-методического комплекса на повышение качества знаний, познавательной самостоятельности студентов.

Целью первого констатирующего этапа (1998-1999г.) явилось создание научно-теоретической базы использования ИССМ в процессе обучения высшей математике и разработка соответствующего учебно-методического комплекса. Для этого была проанализирована психологическая, педагогическая, методическая, математическая и техническая литература по исследуемой проблеме, проведено анкетирование студентов и преподавателей.

Обобщая полученные результаты, мы пришли к выводу, что, начиная с первого курса, следует применять новые компьютерные технологии, которыми являются ИССМ, в преподавании математики при изучении теоретических основ и для решения математических задач, сочетая различные формы аудиторной работы с самостоятельной деятельностью студентов. Теоретическая разработка учебно-методического комплекса на основе ИССМ требует его экспериментальной проверки в процессе обучения курса высшей математики в вузе.

На втором поисковом (1999г.) этапе осуществлялась экспериментальная проверка выдвинутых теоретических положений, предварительная оценка и корректировка разработанной модели по одному из разделов высшей математики – аналитической геометрии, изучаемой на первом курсе. Для этого в процесс обучения высшей математике были включены соответствующие лабораторные работы.

На поисковом этапе была апробирована предложенная методика обучения высшей математике с использованием лабораторных работ на основе ИССМ. Студентами было отмечено, что выполнение лабораторных работ на основе ИССМ помогает точнее понять теоретический материал, и упрощает решение практических задач. Многие обучаемые используют компьютер параллельно с учебником как источник получения необходимой информации, что обеспечивает достаточно высокий уровень усвоения учебного материала. Результаты обработаны с помощью критерия Пирсона и критерия знаков.

На третьем контрольном этапе (1999–2000г) был разработан учебно-методический комплекс на основе ИССМ, включающий методическую модель, программу и содержание лабораторных работ на основе ИССМ для студентов первого курса по основным разделам высшей математике: линейной и векторной алгебре, аналитической геометрии, математическому анализу. При этом мы опирались на теоретические и методические основы преподавания высшей математики с использованием ИССМ, разработанные и апробированные на поисковом и констатирующем этапах эксперимента.

Целью контрольного этапа эксперимента явилась проверка эффективности разработанного учебно-методического комплекса по двум критериям:

1. оценки усвоения знаний по высшей математике (критерий хи-квадрат);
2. уровня познавательной самостоятельности студентов (за основу взята методика использования познавательных единиц В. И. Крупича).

Эксперимент показал, что студенты, обучавшиеся с помощью ИССМ, не только лучше усвоили основные определения, формулы, алгоритмы, но и, что особенно важно, успешнее применяют полученные знания, могут проследить взаимосвязь между основными понятиями курса высшей математики, конструируют алгоритмы решения некоторых задач, указывают приемы их решения с помощью ИССМ. Внедрение системы лабораторных работ на основе ИССМ положительно влияет на развитие познавательной самостоятельности студентов, что приводит к осознанному планированию исследований, связанных с усвоением и применением теоретических знаний, решением математических задач и их проверкой.

В начало