I. Определение, основные свойства и графики
гиперболических функций
В начало
определения ~ гипербола
~ производные ~
вторые производные ~ графики
1. Гиперболическими синусом, косинусом,
тангенсом и котангенсом называются функции :
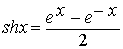 ; ; 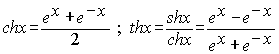 ; ; 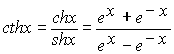 . .
Областью определения функций shx , chx , thx является
вся числовая ось; функция y=cthx не определена в
точке х=0. Название гиперболических функций
(синус, косинус, …) объясняется тем, что для них
справедливы тождества ''похожие'' на
тригонометрические:
ch(x± y)=chx · chy ± shx · shy , (1)
sh(x± y)=shx · chy± chx · shy , (2)
ch2x–sh2x=1 , (3)
ch2x=ch2x+sh2x , (4)
sh2x=2shx · chx . (5)
Тождества (2) и (5) аналогичны соответствующим
формулам тригонометрии, а формулы (1) , (3) и (4)
отличаются от тригонометрических только знаком.
Доказываются тождества (1) – (5) непосредственной
проверкой. Более подробно о тождествах для
гиперболических функций изложено в разделе III.
2. Рассмотрим уравнение гиперболы:
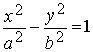
Его можно записать в параметрическом виде,
используя гиперболические функции (этим и
объясняется их название).
Обозначим y= b·sht , тогда х2 / а2=1+sh2t =ch2t . Откуда x=±
a·cht .
Таким образом мы приходим к следующим
параметрическим уравнениям гиперболы :
x= ± a ·cht ,
у= в ·sht , – 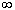 < t < < t < 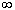 . (6) . (6)
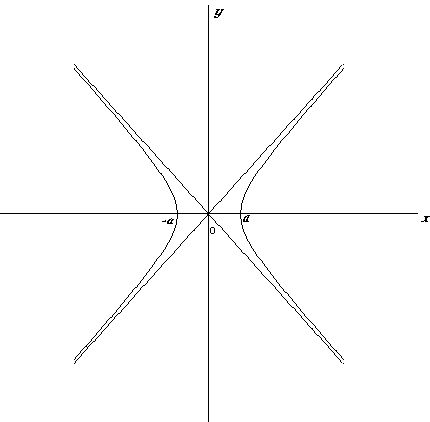
Рис. 1.
Знак ''+'' в верхней формуле (6) соответствует
правой ветви гиперболы, а знак ''– '' - левой (см.
рис. 1). Вершинам гиперболы А(– а ; 0) и В( а ; 0)
соответствует значение параметра t=0.
Для сравнения можно привести параметрические
уравнения эллипса, использующие
тригонометрические функции :
x=а·cost ,
y=в·sint , 0 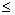 t
t 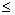 2p . (7) 2p . (7)
3. Очевидно, что функция y=chx является четной и
принимает только положительные значения.
Функция y=shx – нечетная, т.к. :
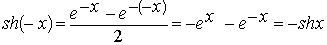 . .
Функции y=thx и y=cthx являются нечетными как частные
четной и нечетной функции. Отметим, что в отличие
от тригонометрических, гиперболические функции
не являются периодическими.
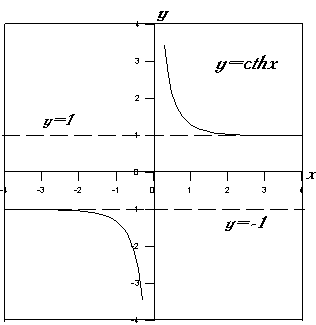
4. Исследуем поведение функции y= cthx в окрестности
точки разрыва х=0:
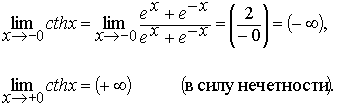
Таким образом ось Оу является вертикальной
асимптотой графика функции y=cthx . Определим
наклонные (горизонтальные) асимптоты :
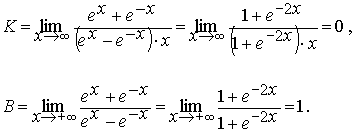
Следовательно, прямая у=1 является правой
горизонтальной асимптотой графика функции y=cthx .
В силу нечетности данной функции ее левой
горизонтальной асимптотой является прямая у= –1.
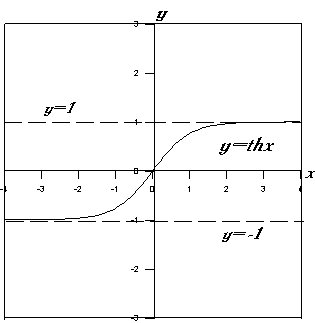
Нетрудно показать, что эти прямые одновременно
являются асимптотами и для функции y=thx. Функции shx
и chx асимптот не имеют.
5. Найдем производные основных гиперболических
функций:
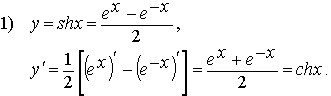
2) (chx)'=shx (показывается аналогично).
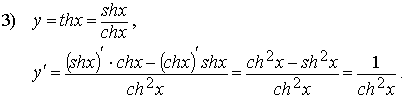
4) 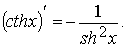
Здесь так же прослеживается
определенная аналогия с тригонометрическими
функциями. Полная таблица производных всех
гиперболических функций приведена в разделе IV.
6. Нетрудно вычислить вторые производные
основных гиперболических функций:
1) 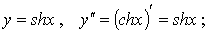
2) 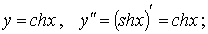
3) 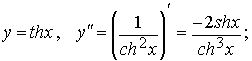
4) 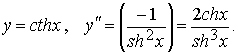
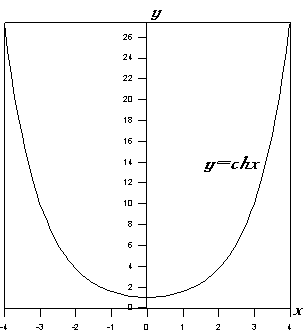
7. Используя результаты п. 1-6, строим
графики основных гиперболических функций:
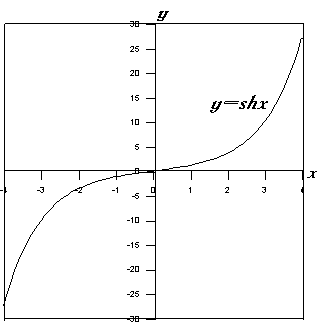
|
|
Рис. 2 |
Рис. 3 |
|
|
| Рис. 4 |
Рис. 5 |
Наверх
В начало | 
