XI. Дифференциальное уравнение изгиба балки на упругом основании

В начало

Рассмотрим дифференциальное уравнение изгиба балки на упругом основании [4]:

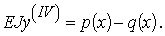
Здесь у=у(х) – прогиб балки, q(x) – реактивные давления упругого основания (нагрузка на основание), р(х) – внешняя нагрузка на балку, E и J– модуль упругости и момент поперечного сечения балки (см. рис. 12).

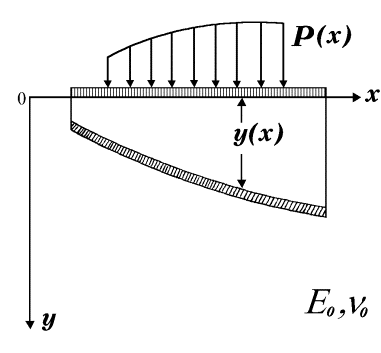
Рис. 12.

Осадка поверхности упругого основания у(х) связана с нагрузкой на основание q(x) законом:

,

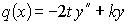где t и k – механические характеристики упругого основания [4] . Считая, что прогиб балки совпадает с осадкой поверхности упругого основания, после исключения из обоих уравнений q(x) получим основное дифференциальное уравнение задачи, выражающее связь между нагрузкой на балку и её прогибом:

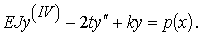
При решении рассматриваемого дифференциального уравнения изгиба балки на упругом основании с двумя характеристиками t и k удобно перейти от действительной координаты х к приведенной координат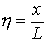е , где

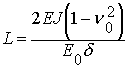
– величина, имеющая размерность длины и называемая упругой характеристикой балки, Е₀ и n₀– модуль упругости и коэффициент Пуассона основания, d – ширина балки. Дифференциальное уравнение окончательно перепишется в виде:

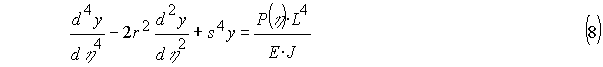
Здесь r² и s⁴ – безразмерные, упругие характеристики, определяемые по формулам:

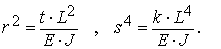
Для решения дифференциального уравнения (8) прежде всего необходимо найти общее решение соответствующего однородного уравнения:

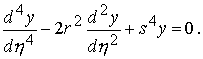
Как указывалось ранее (см. X), общий интеграл однородного дифференциального уравнения четвертого порядка будет иметь вид:

у(h)=с₁у₁(h)+с₂у₂(h)+с₃у₃(h)+с₄у₄(h) ,

где с₁, с₂, с₃, с₄ – произвольные постоянные;

у₁,у₂,у₃,у₄ - линейно независимые функции, определяемые по значениям корней характеристического уравнения:

l⁴-2r²l²+s⁴=0 .

С учетом того, что характеристики r и s не могут быть отрицательными, возможны три случая соотношений между s и r , в соответствии с которыми будут определяться корни характеристического уравнения:

1) s> r> 0 , l_1,2,3,4 =±(a ± b i) ,

где a и b - действительные положительные числа

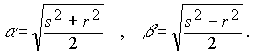
2) s= r , k₁ = k₂ = r , k₃ = k₄ = - r .

3) s< r

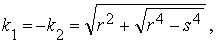
На основании найденных корней характеристического уравнения в табл.1 для удобства сведены выражения функций у_i, i=1,2,3,4.

Таблица 1

 

s , r	y1 (нечетная)	y2 (четная)	y3  (нечетная)	y4  (четная)
s>r	shah cosbh	chah cosbh	chah sinbh	shah sinbh
s=r	shrh	chrh	h chrh	h shrh
s< r	shk1h	chk2h	shk3h	chk4h

Значения k₁ и k₂ , использованные в табл.1, определяются по формулам:

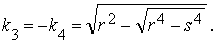
В справочике [5] приведены подробные таблицы числовых значений комбинаций круговых и гиперболических функций (см. табл.1), которые часто встречаются при практических расчетах элементов конструкций. Таблицы составлены для интервала изменения аргумента от 0 до 6p с шагом 0,005 в интервале от 0 до 2p и шагом 0,01 в интервале от 2p до 6p .

Наверх

В начало