Пример 1 ~ Пример 2 ~ Пример 3

Пример 1. Решение системы линейных уравнений методом Якоби.

Пусть дана система уравнений: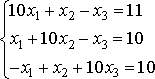    

Требуется найти решение системы с точностью   

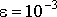
Приведем систему к виду удобному для итерации:   

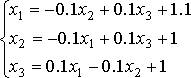
Выберем начальное приближение, например, 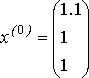     - вектор правой части.

Тогда первая итерация получается так:   

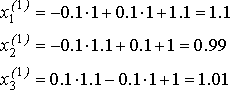
Аналогично получаются следующие приближения к решению.

 ,         ,        

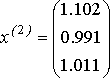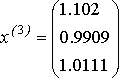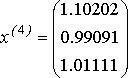
Найдем норму матрицы 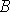.  Будем использовать норму .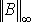

Так как сумма модулей элементов в каждой строке равна 0.2, то 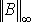= 0.2 < 1/2, поэтому критерий окончания итераций в этой задаче .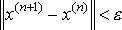

Вычислим нормы разностей векторов:   ,   .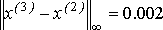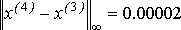

Так как 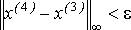 ,  заданная точность достигнута на четвертой итерации.

Ответ:  x ₁ = 1.102,  x ₂ = 0.991,  x ₃ = 1.101

Теоретическая справка

Вернуться на страницу <Введение в вычислительную математику. Примеры>

Пример 2. Решение систем линейных уравнений методом Зейделя.

Рассмотрим параллельно решение 3-х систем уравнений:

,      ,     

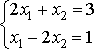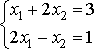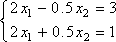
Приведем системы к виду удобному для итераций:

,      ,     

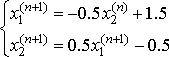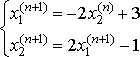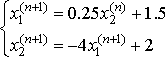
Заметим, что условие сходимости 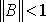   выполнено только для первой системы. Вычислим 3 первых приближения к решению в каждом случае.

1-ая система.      ,      ,      ,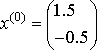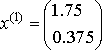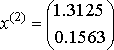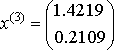     

Точное решение здесь   x ₁ = 1.4,    x ₂ = 0.2. Итерационный процесс сходится.

2-ая система. 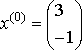   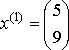  , 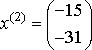   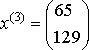  ,      ,        - итерационный процесс разошелся.

Точное решение   x ₁ = 1,    x ₂ = 0.2.

3-я система. 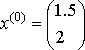   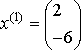  , 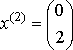   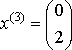  ,      ,        - итерационный процесс зациклился.

Точное решение   x ₁ = 1,    x ₁ = 2.

Для геометрической интерпретации полученных результатов постройте чертеж.

Теоретическая справка

Вернуться на страницу <Введение в вычислительную математику. Примеры>

Пример 3. Решение систем линейных уравнений методом простой итерации.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica
Решение примера в среде пакета Matlab

Вернуться на страницу <Введение в вычислительную математику. Примеры>