Курс "Введение в вычислительную математику"
Данный курс посвящен введению в вычислительную математику.
1. Теория погрешностей и машинная арифметика.
2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.
3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.
4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.
5. Решение систем линейных алгебраических уравнений прямыми методами.
6. Решение систем линейных алгебраических уравнений итерационными методами.
7. Приближение функций. Метод наименьших квадратов.
8. Приближение функций. Интерполяция.
9. Приближение функций. Сплайны.
10. Решение задачи Коши одношаговыми методами.
1. Теория погрешностей и машинная арифметика.
Пусть ![]() - точное значение,
- точное значение,
![]() - приближенное значение некоторой величины.
- приближенное значение некоторой величины.
Абсолютной погрешностью приближенного значения ![]() называется величина
называется величина ![]() .
.
Относительной погрешностью значения ![]() (при
(при ![]() 0) называется величина
0) называется величина ![]() .
.
Так как, значение ![]() как правило неизвестно, чаще получают оценки погрешностей вида:
как правило неизвестно, чаще получают оценки погрешностей вида: ![]()
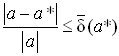 .
.
Величины ![]() и
и ![]() называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Значащими цифрами числа ![]() называют все цифры в его записи, начиная с первой ненулевой слева.
называют все цифры в его записи, начиная с первой ненулевой слева.
Значащую цифру числа ![]() называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Для оценки погрешностей арифметических операций следует использовать следующие утверждения:
Абсолютная погрешность алгебраической суммы (суммы или разности ) не превосходит суммы абсолютной погрешности слагаемых, т.е.
![]()
Если а и b - ненулевые числа одного знака, то справедливы неравенства
![]() ,
, ![]() ,
,
где ![]() ,
, ![]()
Для относительных погрешностей произведения и частного приближенных чисел верны оценки:
если ![]() и
и ![]() , то
, то ![]() ,
, ![]() .
.
Пусть ![]() - дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов
- дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов ![]() . Тогда для абсолютной погрешности функции
. Тогда для абсолютной погрешности функции ![]() справедлива следующая оценка
справедлива следующая оценка
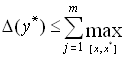
![]() .
.
Здесь [x, x*] v отрезок, соединяющий точки x и x* =( ![]() )
)
Для относительной погрешности функции справедливо следующее приближенное равенство
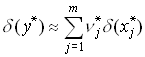 , где
, где 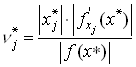
2. Решение нелинейных уравнений. Методы бисекций, простой итерации, Ньютона.
Пусть рассматривается уравнение ![]() . Корнем уравнения называется значение
. Корнем уравнения называется значение ![]() , при котором
, при котором ![]() . Корень
. Корень ![]() называется простым, если
называется простым, если
![]() , в противном случае корень называется кратным. Целое число m называется кратностью корня
, в противном случае корень называется кратным. Целое число m называется кратностью корня ![]() , если
, если ![]() для k=1,2,3-,m-1 и
для k=1,2,3-,m-1 и
![]() .
.
Постановка задачи вычисления приближенного значения корня с точностью ![]() : найти такое значения
: найти такое значения ![]() , что
, что ![]() .
.
Решение задачи разбивается на два этапа: на первом этапе осуществляют локализацию корней, на втором этапе производят итерационное уточнение корней. На этапе локализации корней находят достаточно узкие отрезки ( или отрезок, если корень единственный), которые содержат один и только один корень уравнения ![]() . На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.
. На втором этапе вычисляют приближенное значение корня с заданной точностью. Часто вместо отрезка локализации достаточно указать начальное приближение к корню.
Метод бисекции. Пусть [a,b] v отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков ![]() .
.
Алгоритм метода бисекции состоит в построении последовательности вложенных отрезков, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Опишем один шаг итераций метода. Пусть на k-ом шаге найден отрезок ![]() такой, что
такой, что ![]() . Найдем середину отрезка
. Найдем середину отрезка .gif) . Если
. Если ![]() , то
, то ![]() - корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:
- корень и задача решена. Если нет, то из двух половин отрезка выбираем ту, на концах которой функция имеет противоположные знаки:
![]() ,
, ![]() , если
, если ![]()
![]() ,
, ![]() , если
, если ![]()
Критерий окончания итерационного процесса: если длина отрезка локализации меньше 2![]() , то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.
, то итерации прекращают и в качестве значения корня с заданной точностью принимают середину отрезка.
Теорема о сходимости метода бисекций. Пусть функция f(x) непрерывна на [a,b] и на концах принимает значения разных знаков ![]() .Тогда метод сходится и справедлива оценка погрешности :
.Тогда метод сходится и справедлива оценка погрешности : ![]()
Метод Ньютона (метод касательных) . Расчетная формула метода Ньютона имеет вид:
.gif) . Геометрически метод Ньютона означает, что следующее приближение к корню
. Геометрически метод Ньютона означает, что следующее приближение к корню ![]() есть точка пересечения с осью ОХ
есть точка пересечения с осью ОХ
касательной, проведенной к графику функции y=f(x) в точке ![]() .
.
Теорема о сходимости метода Ньютона. Пусть ![]() - простой корень уравнения
- простой корень уравнения ![]() , в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая
, в некоторой окрестности которого функция дважды непрерывно дифференцируема. Тогда найдется такая малая ![]() - окрестность корня
- окрестность корня ![]() , что при произвольном выборе начального приближения
, что при произвольном выборе начального приближения ![]() из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка
из этой окрестности итерационная последовательность метода Ньютона не выходит за пределы окрестности и справедлива оценка
![]() , где
, где ![]() ,
, ![]() .
.
Критерий окончания итерационного процесса. При заданной точности ![]() >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство
>0 вычисления следует вести до тех пор пока не окажется выполненным неравенство ![]() .
.
Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня ![]() . Неудачный выбор может дать расходящуюся итерационную последовательность.
. Неудачный выбор может дать расходящуюся итерационную последовательность.
Метод простой итерации (метод последовательных повторений). Для применения метода простой итерации следует исходное уравнение ![]() преобразовать к виду, удобному для итерации
преобразовать к виду, удобному для итерации ![]() . Это преобразование можно выполнить различными способами. Функция
. Это преобразование можно выполнить различными способами. Функция ![]() называется итерационной функцией. Расчетная формула метода простой итерации имеет вид:
называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: ![]() .
.
Теорема о сходимости метода простой итерации. Пусть в некоторой ![]() - окрестности корня
- окрестности корня ![]() функция
функция ![]() дифференцируема и удовлетворяет неравенству
дифференцируема и удовлетворяет неравенству ![]() , где
, где ![]() - постоянная . Тогда независимо от выбора начального приближения из указанной
- постоянная . Тогда независимо от выбора начального приближения из указанной ![]() - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится
- окрестности итерационная последовательность не выходит из этой окрестности, метод сходится
со скоростью геометрической последовательности и справедлива оценка погрешности: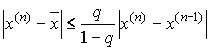 ,
, ![]() .
.
Критерий окончания итерационного процесса. При заданной точности ![]() >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство
>0 вычисления следует вести до тех пор пока не окажется выполненным неравенство 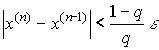 . Если величина
. Если величина ![]() , то можно использовать более простой критерий окончания итераций:
, то можно использовать более простой критерий окончания итераций: ![]() .
.
Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду ![]() . Предположим дополнительно, что производная
. Предположим дополнительно, что производная ![]() знакопостоянна и
знакопостоянна и ![]() на отрезке [a,b]. Тогда при выборе итерационного параметра
на отрезке [a,b]. Тогда при выборе итерационного параметра ![]() метод сходится и значение
метод сходится и значение
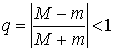 .
.
3. Решение нелинейных уравнений. Обусловленность задачи нахождения корня. Интервал неопределенности.
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям входных данных.
Пусть установлено неравенство ![]() , где
, где ![]() - относительная погрешность входных данных, а
- относительная погрешность входных данных, а ![]() - относительная погрешность решения. Тогда
- относительная погрешность решения. Тогда ![]() - называется абсолютным числом обусловленности задачи. Если же установлено неравенство
- называется абсолютным числом обусловленности задачи. Если же установлено неравенство ![]() между относительными погрешностями данных и решения, то
между относительными погрешностями данных и решения, то ![]() называют относительным числом обусловленности задачи.
называют относительным числом обусловленности задачи.
Обычно под числом обусловленности ![]() понимают относительное число обусловленности. Если
понимают относительное число обусловленности. Если ![]() , то задачу называют плохо обусловленной.
, то задачу называют плохо обусловленной.
Обусловленность задачи нахождения корня. Пусть ![]() v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции
v корень, подлежащий определению. Будем считать, что входными данными для задачи вычисления корня являются значения функции ![]() . Так как
. Так как ![]() v вычисляется приближенно, то обозначим функцию, полученную в действительности через
v вычисляется приближенно, то обозначим функцию, полученную в действительности через ![]() . Предположим, что в малой окрестности корня выполняется неравенство:
. Предположим, что в малой окрестности корня выполняется неравенство: ![]() . Для близких к
. Для близких к ![]() значений
значений ![]() справедливо равенство
справедливо равенство ![]() , следовательно,
, следовательно, 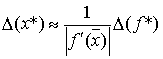 . Это означает, что число обусловленности задачи нахождения корня равно
. Это означает, что число обусловленности задачи нахождения корня равно 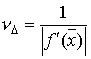 . Из последней формулы следует, что чем меньше значение производной функции в точке корня, тем задача хуже обусловлена. В частности, задача нахождения кратного корня имеет число обусловленности - бесконечность.
. Из последней формулы следует, что чем меньше значение производной функции в точке корня, тем задача хуже обусловлена. В частности, задача нахождения кратного корня имеет число обусловленности - бесконечность.
Интервал неопределенности корня. Если функция ![]() непрерывна, то найдется такая малая окрестность
непрерывна, то найдется такая малая окрестность ![]() корня
корня ![]() , имеющая радиус
, имеющая радиус ![]() , в которой выполнено неравенство
, в которой выполнено неравенство ![]() . Это означает, что
. Это означает, что ![]()
![]() знак вычисленного значения
знак вычисленного значения ![]() , вообще говоря не обязан совпадать со знаком
, вообще говоря не обязан совпадать со знаком ![]() и, следовательно, становится невозможным определить, какое именно значение
и, следовательно, становится невозможным определить, какое именно значение ![]() из интервала
из интервала ![]() обращает функцию
обращает функцию ![]() в нуль. Этот интервал называется интервалом неопределенности корня. Очевидно, что радиус интервала неопределенности для простого корня равен
в нуль. Этот интервал называется интервалом неопределенности корня. Очевидно, что радиус интервала неопределенности для простого корня равен 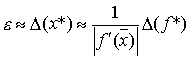 . Аналогично можно показать, что для кратного корня
. Аналогично можно показать, что для кратного корня 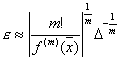 . Это означает, что для простого корня радиус интервала неопределенности прямо пропорционален погрешности вычисления функции
. Это означает, что для простого корня радиус интервала неопределенности прямо пропорционален погрешности вычисления функции ![]() , а для кратного корня
, а для кратного корня ![]() .
.
Пусть ![]() . Корень уравнения простой и равен
. Корень уравнения простой и равен ![]() = -0.34729635533861. Тогда
= -0.34729635533861. Тогда ![]() и
и ![]() . Если
. Если ![]() , то
, то ![]() . Это означает , что найти корень с точностью меньшей, чем радиус интервала неопределенности, не удастся.
. Это означает , что найти корень с точностью меньшей, чем радиус интервала неопределенности, не удастся.
Применение метода Ньютона для нахождения кратного корня. Метод Ньютона для случая кратного корня обладает лишь линейной скоростью сходимости. Чтобы сохранить квадратичную сходимость его модифицируют следующим образом:
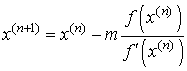 , где
, где ![]() - кратность корня.
- кратность корня.
Как правило, значение ![]() v неизвестно. Используя метод Ньютона, можно узнать кратность корня. Для этого будем задавать значения
v неизвестно. Используя метод Ньютона, можно узнать кратность корня. Для этого будем задавать значения ![]() = 1,2,3 и вычислять значение корня с заданной точностью , одновременно подсчитывая количество итераций для каждого значения
= 1,2,3 и вычислять значение корня с заданной точностью , одновременно подсчитывая количество итераций для каждого значения ![]() . При некотором значении
. При некотором значении ![]() число итераций будет минимальным. Это значение
число итераций будет минимальным. Это значение ![]() и есть кратность корня.
и есть кратность корня.
4. Решение систем линейных алгебраических уравнений. Нормы векторов и матриц. LU-разложение матрицы.
Нормы векторов и матриц. Обозначим через ![]() - точное решение системы, а через
- точное решение системы, а через ![]() - приближенное решение системы. Для количественной характеристики вектора погрешности
- приближенное решение системы. Для количественной характеристики вектора погрешности ![]() введем понятие нормы.
введем понятие нормы.
Нормой вектора ![]() называется число
называется число ![]() , удовлетворяющее трем аксиомам:
, удовлетворяющее трем аксиомам:
1) ![]() причем
причем ![]() = 0 тогда и только тогда, когда
= 0 тогда и только тогда, когда ![]() = 0;
= 0;
2) ![]() для любого вектора
для любого вектора ![]() и любого числа
и любого числа ![]() ;
;
3) ![]() для любых векторов
для любых векторов ![]() и
и ![]() .
.
Наиболее употребительными являются следующие три нормы:
![]() ,
, .gif) ,
, ![]() .
.
Абсолютная и относительная погрешности вектора вводятся с помощью формул:
![]() и
и .gif) .
.
Нормой матрицы ![]() называется величина
называется величина .gif) . Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:
. Введенная норма обладает свойствами, аналогичными свойствам нормы вектора:
1) ![]() причем
причем ![]() = 0 тогда и только тогда, когда A = 0;
= 0 тогда и только тогда, когда A = 0;
2) ![]() для любой матрицы A и любого числа
для любой матрицы A и любого числа ![]() ;
;
3) ![]() для любых матриц A и B;
для любых матриц A и B;
4) ![]() .
.
Каждой из векторных норм соответствует своя подчиненная норма матрицы:
![]() ,
, ![]() ,
, ![]() .
.
В оценках вместо нормы ![]() используется евклидова норма матрицы
используется евклидова норма матрицы
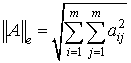 , так как
, так как ![]() .
.
Абсолютная и относительная погрешности матрицы вводятся аналогично погрешностям вектора с помощью формул:
![]() ,
, .gif) .
.
Пусть рассматривается система линейных алгебраических уравнений
.gif)
![]()
В матричной форме записи она имеет вид ![]() . Будем предполагать, что матрица системы
. Будем предполагать, что матрица системы ![]() задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.
задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво по входным данным.
Обусловленность задачи. Так же как и другие задачи, задача вычисления решения системы может быть как хорошо обусловленной, так и плохо обусловленной.
Теорема об оценке погрешности решения по погрешностям входных данных.
Пусть решение системы ![]() , а x* - решение системы A*x*=b*, тогда
, а x* - решение системы A*x*=b*, тогда ![]() , где
, где ![]() - относительное число обусловленности системы.
- относительное число обусловленности системы.
Если число обусловленности больше 10, то система является плохо обусловленной, так как возможен сильный рост погрешности результата.
Метод Гаусса. Рассмотрим метод Гаусса (схему единственного деления) решения системы уравнений. Прямой ход состоит из m-1 шагов исключения.
1 Шаг. Исключим неизвестное ![]() из уравнений с номерами i = 2,3,..m. Предположим, что
из уравнений с номерами i = 2,3,..m. Предположим, что ![]() . Будем называть его ведущим элементом 1-го шага.
. Будем называть его ведущим элементом 1-го шага.
Найдем величины ![]() , i=2,3,...m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, ...m vго уравнений системы первое уравнение, умноженное соответственно на
, i=2,3,...m , называемые множителями 1-го шага. Вычтем последовательно из второго, третьего, ...m vго уравнений системы первое уравнение, умноженное соответственно на ![]() . В результате 1-го шага получим эквивалентную систему уравнений:
. В результате 1-го шага получим эквивалентную систему уравнений:
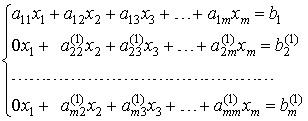
Аналогично проводятся остальные шаги. Опишем очередной k-ый шаг. Предположим, что ведущий элемент ![]() . Вычислим множители к-го шага:
. Вычислим множители к-го шага:![]() , i=k+1,...m и вычтем последовательно из (k+1)-го, ...m v го уравнений системы k-ое уравнение, умноженное соответственно на
, i=k+1,...m и вычтем последовательно из (k+1)-го, ...m v го уравнений системы k-ое уравнение, умноженное соответственно на
![]() .После (m-1)-го шага исключения получим систему уравнений
.После (m-1)-го шага исключения получим систему уравнений
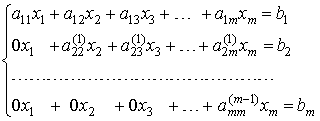 ,
,
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы находим ![]() . Подставляя найденное значение
. Подставляя найденное значение ![]() в предпоследнее уравнение, получим
в предпоследнее уравнение, получим ![]() . Далее последовательно находим неизвестные
. Далее последовательно находим неизвестные ![]() .
.
LU разложение матрицы. Представим матрицу A в виде произведения нижней треугольной матрицы L и верхней треугольной U.
Введем в рассмотрение матрицы
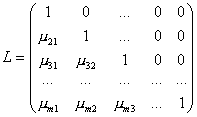 и
и ![]()

Можно показать, что A = LU. Это и есть разложение матрицы на множители.
5. Решение систем линейных алгебраических уравнений прямыми методами.
Метод решения задачи называют прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Если эта последовательность сходится к решению задачи, то говорят, что итерационный процесс сходится. К прямым методам решения относятся метод Гаусса и его модификации, метод Холецкого и метод прогонки.
В методе Гаусса для вычисления масштабирующих множителей требуется делить на ведущие элементы каждого шага. Если элемент равен нулю или близок к нулю, то возможен неконтролируемый рост погрешности.
Поэтому часто применяют модификации метода Гаусса, обладающие лучшими вычислительными свойствами.
Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент ![]() при неизвестной
при неизвестной ![]() в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером
в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером ![]() , меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента
, меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента ![]() . После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.
. После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.
Метод Холецкого. Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A=![]() . Если разложение получено, то как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами:
. Если разложение получено, то как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами: ![]() и
и ![]() . Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы
. Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы ![]() приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:
приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:
![]() ,
, ![]() i = 2, 3, ..., m,
i = 2, 3, ..., m,
![]() ,
, ![]() i = 3, 4, ..., m,
i = 3, 4, ..., m,
...............
![]()
![]() i = k+1, ... , m.
i = k+1, ... , m.
![]()
Метод прогонки.Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:
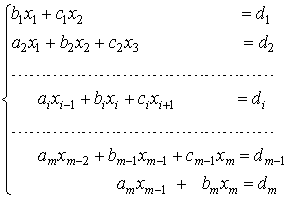
Преобразуем первое уравнение системы к виду ![]() , где
, где ![]() ,
, ![]()
Подставим полученное выражение во второе уравнение системы и преобразуем его к виду ![]() и т.д. На i-ом шаге уравнение преобразуется к виду
и т.д. На i-ом шаге уравнение преобразуется к виду ![]() , где
, где ![]() ,
, ![]() . На m-ом шаге подстановка в последнее уравнение выражения
. На m-ом шаге подстановка в последнее уравнение выражения ![]() дает возможность определить значение
дает возможность определить значение ![]() :
:
![]() . Значения остальных неизвестных находятся по формулам:
. Значения остальных неизвестных находятся по формулам: ![]() , i = m-1, m-2, ..., 1.
, i = m-1, m-2, ..., 1.
6. Решение систем линейных алгебраических уравнений итерационными методами.
Рассматривается система Ax = b.
Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений
![]() и находится последовательность приближений к корню. Для сходимостиитерационного процесса достаточно, чтобы было выполнено условие
и находится последовательность приближений к корню. Для сходимостиитерационного процесса достаточно, чтобы было выполнено условие ![]() . Критерий окончания итераций зависит от применяемого итерационного метода.
. Критерий окончания итераций зависит от применяемого итерационного метода.
Метод Якоби.
Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное x1, из второго уравнения системы выразим x2, и т. д. В результате получим систему уравнений с матрицей B, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:
![]() ,i, j = 1, 2, ... n.
,i, j = 1, 2, ... n.
Компоненты вектора d вычисляются по формулам:
![]() , i = 1, 2, ... n.
, i = 1, 2, ... n.
Расчетная формула метода простой итерации имеет вид
![]() ,
,
или в покоординатной форме записи выглядит так:
![]() , i = 1, 2, ... m.
, i = 1, 2, ... m.
Критерий окончания итераций в методе Якоби имеет вид:
![]() , где
, где 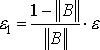 .
.
Если ![]() , то можно применять более простой критерий
, то можно применять более простой критерий
![]() окончания итераций
окончания итераций
Метод Зейделя.
Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному xi при i >1 используют уже найденные (n+1)-е приближения к неизвестным x1, x2, ..., xi - 1, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:
![]() ,
,
i = 1, 2, ... m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.
Пусть матрица системы уравнений A - симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.
Метод простой итерации.
Если A - симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду:
x = x - ![]() (Ax - b),
(Ax - b), ![]() - итерационный параметр.
- итерационный параметр.
Расчетная формула метода простой итерации в этом случае имеет вид:
x (n+1) = x n - ![]() (Ax n - b).
(Ax n - b).
Здесь B = E - ![]() A и параметр
A и параметр ![]() > 0 выбирают так, чтобы по возможности сделать минимальной величину
> 0 выбирают так, чтобы по возможности сделать минимальной величину ![]() .
.
Пусть ![]() и
и ![]() - минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра
- минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра ![]() . В этом случае
. В этом случае ![]() принимает минимальное значение равное
принимает минимальное значение равное ![]() .
.
7. Приближение функций. Метод наименьших квадратов.
На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны.
Ниже рассматривается решение задачи приближения многочленами таблично заданной функции по методу наименьших квадратов и по методу интерполяции.
Постановка задачи приближения функции по методу наименьших квадратов. Пусть функция y=f(x) задана таблицей своих значений: ![]() , i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО)
, i=0,1,-n. Требуется найти многочлен фиксированной степени m, для которого среднеквадратичное отклонение (СКО) .gif) минимально.
минимально.
Так как многочлен ![]() определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов
определяется своими коэффициентами, то фактически нужно подобрать набор кофициентов ![]() , минимизирующий функцию
, минимизирующий функцию .gif) .
.
Используя необходимое условие экстремума, ![]() , k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов:
, k=0,1,-m получаем так называемую нормальную систему метода наименьших квадратов: ![]() , k=0,1,-m.
, k=0,1,-m.
Полученная система есть система алгебраических уравнений относительно неизвестных ![]() . Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
. Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса.
Запишем нормальную систему наименьших квадратов для двух простых случаев: m=0 и m=2. При m=0 многочлен примет вид: ![]() . Для нахождения неизвестного коэффициента
. Для нахождения неизвестного коэффициента ![]() имеем уравнение:
имеем уравнение:.gif) . Получаем, что коэффициент
. Получаем, что коэффициент ![]() есть среднее арифметическое значений функции в заданных точках.
есть среднее арифметическое значений функции в заданных точках.
Если же используется многочлен второй степени ![]() , то нормальная система уравнений примет вид:
, то нормальная система уравнений примет вид:
.gif)
Предположим, что функцию f можно с высокой точностью аппроксимировать многочленом ![]() некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные
некоторой степени m. Если эта степень заранее неизвестна, то возникает проблема выбора оптимальной степени аппроксимирующего многочлена в условиях, когда исходные данные ![]() содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина
содержат случайные ошибки. Для решения этой задачи можно принять следующий алгоритм: для каждого m=0,1,2,.. вычисляется величина
.gif) . За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина
. За оптимальное значение степени многочлена следует принять то значение m, начиная с которого величина ![]() стабилизируется или начинает возрастать.
стабилизируется или начинает возрастать.
Определение параметров эмпирической зависимости. Часто из физических соображений следует, что зависимость ![]() между величинами хорошо описывается моделью вида
между величинами хорошо описывается моделью вида ![]() , где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров
, где вид зависимости g известен. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров ![]() из условия минимума функции:
из условия минимума функции: ![]() .
.
Если зависимость от параметров ![]() нелинейна, то экстремум функции
нелинейна, то экстремум функции ![]() ищут методами минимизации функций нескольких переменных.
ищут методами минимизации функций нескольких переменных.
8. Приближение функций. Интерполяция.
Постановка задачи интерполяции функций.
Пусть функция y = f(x) задана таблицей своих значений:
![]() , i=0,1,...n. Требуется найти многочлен степени n, такой, что значения функции и многочлена в точках таблицы совпадают:
, i=0,1,...n. Требуется найти многочлен степени n, такой, что значения функции и многочлена в точках таблицы совпадают:
![]() , i=0,1,... n.
, i=0,1,... n.
Справедлива теорема о существовании и единственности интерполяционного многочлена.
Одна из форм записи интерполяционного многочлена - многочлен Лагранжа:
![]() , где
, где
.gif)
Многочлен ![]() представляет собой многочлен степени n , удовлетворяющий условию
представляет собой многочлен степени n , удовлетворяющий условию
![]() .
.
Таким образом, степень многочлена ![]() равна n и при
равна n и при ![]() в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером
в сумме обращаются в нуль все слагаемые, кроме слагаемого с номером ![]() , равного
, равного ![]() . Поэтому многочлен Лагранжа является интерполяционным.
. Поэтому многочлен Лагранжа является интерполяционным.
Другая форма записи интерполяционного многочлена - интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция f задана с произвольным шагом и
точки таблицы занумерованы в произвольном порядке. Величины
![]() называют разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:
называют разделенными разностями первого порядка. Разделенные разности второго порядка определяются формулой:
![]() .
.
Определение разделенной разности порядка ![]() таково:
таково:
![]() .
.
Используя разделенные разности, интерполяционный многочлен Ньютона можно записать в следующем виде:
![]()
![]()
Величину ![]() называют погрешностью интерполяции или остаточным членом интерполяции.
называют погрешностью интерполяции или остаточным членом интерполяции.
Оценка погрешности интерполяции.
Если функция n+1 раз на отрезке [a,b] , содержащем узлы интерполяции ![]() , i=0,1,...n, то для погрешности интерполяции справедлива оценка:
, i=0,1,...n, то для погрешности интерполяции справедлива оценка:
![]() . Здесь
. Здесь ![]() ,
, ![]() .
.
Эта оценка показывает, что для достаточно гладкой функции при фиксированной степени интерполяционного многочлена погрешность интерполяции стремится к нулю не медленнее, чем величина, пропорциональная ![]() . Этот факт формулируют так: интерполяционный многочлен степени nаппроксимирует функцию с (n+1) порядком точности относительно
. Этот факт формулируют так: интерполяционный многочлен степени nаппроксимирует функцию с (n+1) порядком точности относительно ![]() .
.
В практическом плане формула Ньютона обладает преимуществами перед формулой Лагранжа. Предположим, что в необходимо увеличить степень многочлена на единицу, добавив в таблицу еще один узел ![]() . При использовании формулы Лагранжа это приводит к необходимости вычислять каждое слагаемое заново. Для вычисления
. При использовании формулы Лагранжа это приводит к необходимости вычислять каждое слагаемое заново. Для вычисления ![]() достаточно добавить к
достаточно добавить к ![]() лишь очередное слагаемое:
лишь очередное слагаемое: ![]() . Если функция f достаточно гладкая, то справедливо приближенное равенство
. Если функция f достаточно гладкая, то справедливо приближенное равенство ![]() . Это равенство можно использовать для практической оценки погрешности интерполяции :
. Это равенство можно использовать для практической оценки погрешности интерполяции :![]() .
.
9. Приближение функций. Сплайны.
Глобальная и кусочно-полиномиальная интерполяция. Пусть функция f(x) интерполируется на отрезке [a,b]. Метод решения этой задачи с помощью единого многочлена ![]() для всего отрезка называют глобальной полиномиальной интерполяцией. В вычислительной практике такой поход применяется редко в силу различных причин. Одна из причин v необходимо задать стратегию выбора узлов при интерполяции функции f многочленами все возрастающей степени n.
для всего отрезка называют глобальной полиномиальной интерполяцией. В вычислительной практике такой поход применяется редко в силу различных причин. Одна из причин v необходимо задать стратегию выбора узлов при интерполяции функции f многочленами все возрастающей степени n.
Теорема Фабера. Какова бы ни была стратегия выбора узлов интерполяции, найдется непрерывная на отрезке [a,b] функция f, для которой ![]() при
при ![]() . Таким образом, теорема Фабера отрицает существование единой для всех непрерывных функций стратегии выбора узлов. Проиллюстрируем сказанное примером.
. Таким образом, теорема Фабера отрицает существование единой для всех непрерывных функций стратегии выбора узлов. Проиллюстрируем сказанное примером.
Предположим, что выбираем равноотстоящие узлы, то есть ![]() , i = 0,1,...n, где
, i = 0,1,...n, где ![]() . Покажем, что для функции Рунге такая стратегия является неудачной.
. Покажем, что для функции Рунге такая стратегия является неудачной.
На практике чаще используют кусочно-полиномиальную интерполяцию: исходный отрезок разбивается на части и на каждом отрезке малой длины исходная функция заменяется многочленом невысокой степени. Система Mathcad предоставляет возможность аппроксимации двумя важными классами функций: кусочно-линейной и сплайнами.
При кусочно-линейной интерполяции узловые точки соединяются отрезками прямых, то есть через каждые две точки ![]() ,
, ![]() проводится полином первой степени.
проводится полином первой степени.
Как видно из приведенного примера этот способ приближения также имеет недостаток: в точках "стыка" двух соседних многочленов производная, как правило, имеет разрыв.
Если исходная функция была гладкой и требуется, чтобы и аппроксимирующая функция была гладкой, то кусочно-полиномиальная интерполяция неприемлема. В этом случае применяют сплайны v специальным образом построенные гладкие кусочно-многочленные функции.
Интерполяция сплайнами. Пусть отрезок [a,b] разбит точками на n частичных отрезков ![]() . Сплайном степени m называется функция
. Сплайном степени m называется функция ![]() , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) функция ![]() непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка p.
непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка p.
2) на каждом частичном отрезке ![]() функция совпадает с некоторым алгебраическим многочленом
функция совпадает с некоторым алгебраическим многочленом ![]() степени m.
степени m.
Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a,b] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [a,b] сама функция ![]() (нулевая производная) непрерывна. В то же время на каждом частичном отрезке
(нулевая производная) непрерывна. В то же время на каждом частичном отрезке ![]() совпадает с некоторым многочленом первой степени.
совпадает с некоторым многочленом первой степени.
Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны) ![]() с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.
с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.
Погрешность приближения кубическими сплайнами. Пусть функция f имеет на отрезке [a,b] непрерывную производную четвертого порядка и ![]() . Тогда для интерполяционного кубического сплайна справедлива оценка погрешности:
. Тогда для интерполяционного кубического сплайна справедлива оценка погрешности: ![]() .
.
10. Решение задачи Коши одношаговыми методами.
Постановка задачи Коши для дифференциального уравнения первого порядка.
Пусть дано дифференциальное уравнение первого порядка ![]() . Требуется найти функцию
. Требуется найти функцию ![]() , удовлетворяющую при
, удовлетворяющую при ![]() дифференциальному уравнению и при
дифференциальному уравнению и при ![]() начальному условию
начальному условию ![]() .
.
Теорема существования и единственности задачи Коши. Пусть функция ![]() определена и непрерывна на множестве точек
определена и непрерывна на множестве точек ![]() . Предположим также, что она удовлетворяет условию Липшица:
. Предположим также, что она удовлетворяет условию Липшица: ![]() для всех
для всех ![]() и произвольных
и произвольных ![]() ,
, ![]() , где
, где ![]() - некоторая константа (постоянная Липшица). Тогда для каждого начального значения
- некоторая константа (постоянная Липшица). Тогда для каждого начального значения ![]() существует единственное решение
существует единственное решение ![]() задачи Коши, определенное на отрезке
задачи Коши, определенное на отрезке ![]() .
.
Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку ![]()
Численное решение задачи Коши методом Эйлера.
Численное решение задачи Коши состоит в построении таблицы приближенных значений ![]() в точках
в точках ![]() . Точки
. Точки ![]() ,
, ![]() называются узлами сетки, а величина
называются узлами сетки, а величина ![]() - шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной:
- шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной: ![]() . Разрешая уравнение относительно
. Разрешая уравнение относительно ![]() , получаем расчетную формулу метода Эйлера:
, получаем расчетную формулу метода Эйлера: ![]() ,
, ![]() .
.
Численный метод называется явным, если вычисление решения в следующей точке ![]() осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке
осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке ![]() производится с использованием только одного предыдущего значения
производится с использованием только одного предыдущего значения ![]() . Метод Эйлера является явным одношаговым методом.
. Метод Эйлера является явным одношаговым методом.
Оценка погрешности метода Эйлера.
Локальной погрешностью метода называется величина ![]() . Найдем величину локальной погрешности метода Эйлера:
. Найдем величину локальной погрешности метода Эйлера: ![]() , при условии, что
, при условии, что ![]() . Другими словами
. Другими словами ![]() погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью (или просто погрешностью) численного метода называют сеточную функцию
погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью (или просто погрешностью) численного метода называют сеточную функцию ![]() со значениями
со значениями ![]() в узлах. В качестве меры абсолютной погрешности метода примем величину
в узлах. В качестве меры абсолютной погрешности метода примем величину ![]() . Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид
. Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид ![]() следует, что
следует, что ![]() , где
, где ![]() и M - некоторые константы. Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью
и M - некоторые константы. Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью ![]() требуется найти такое приближенное решение
требуется найти такое приближенное решение ![]() , для которого величина глобальной погрешности
, для которого величина глобальной погрешности ![]() . Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.
. Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.
Правило Рунге оценки погрешностей. Для практической оценки погрешности проводят вычисления с шагами h и h/2. За оценку погрешности решения, полученного с шагом h/2, принимают величину, равную 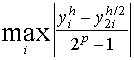 , где p - порядок метода.
, где p - порядок метода.
Модификации метода Эйлера.
Метод Эйлера обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности. Второй порядок точности по ![]() имеет усовершенствованный метод Эйлера :
имеет усовершенствованный метод Эйлера : ![]() . Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке
. Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом ломаных, так как интегральная кривая на отрезке ![]() заменяется ломаной с угловым коэффициентом
заменяется ломаной с угловым коэффициентом ![]() . В усовершенствованном методе Эйлера интегральная кривая на отрезке
. В усовершенствованном методе Эйлера интегральная кривая на отрезке ![]() заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка
заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка ![]() . Так как значение
. Так как значение ![]() в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом
в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом ![]() .
.
Еще одна модификация метода Эйлера второго порядка - метод Эйлера-Коши:
![]()
Решение систем дифференциальных уравнений методом Эйлера.
Пусть требуется решить нормальную систему дифференциальных уравнений:
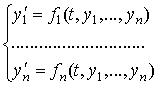
с начальными условиями: ![]() ,
, ![]() , ...,
, ..., ![]()
Эту систему в векторной форме можно записать в виде: ![]() ,
, ![]() . Здесь
. Здесь 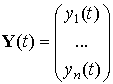 ,
, 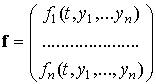 ,
, 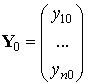 . Расчетная формула метода Эйлера имеет вид:
. Расчетная формула метода Эйлера имеет вид: ![]() ,
, ![]() .
.
Комментарии