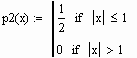| Пример 3. Вычислим эксцесс для двух
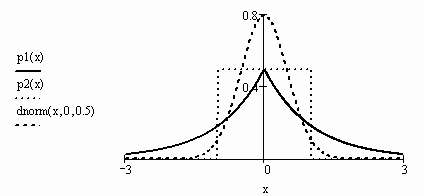
величин, первая из которых имеет распределение Лапласа (плотность вероятностей p(x) = 1/2 exp(-|x|)), а вторая распределена равномерно на отрезке [-1, 1]. Для сравнения вместе с графиками плотности вероятностей исследуемых случайных величин приведем график плотности вероятностей нормального распределения N(0, 1). |
Определим плотности распределения случайных величин
![]()
![]()
![]()
Вычислим центральные моменты второго порядка
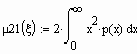
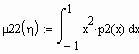
Вычислим центральные моменты четвертого
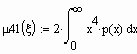
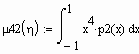
Вычислим эксцессы
![]()
![]()
![]()
![]()
Определим плотности распределения случайных величин и построим их графики.
Для сравнения построим график плотности распределения стандартного нормального распределения.

![]()