Курс по теории вероятностей
Краткий курс по теории вероятностей с примерами. Примеры, приведенные в конце, рассмотрены в среде MATLAB.
Содержание
Случайные величины. Функции распределения, их свойства.
Числовые характеристики случайных величин.
Наиболее распространённые распределения дискретных случайных величин.
Наиболее распространённые распределения непрерывных случайных величин.
Предельные теоремы для биномиального распределения.
Совместные распределения нескольких случайных величин.
Числовые характеристики двумерных случайных величин.
Основные инструменты Mathcad для решения задач теории вероятностей.
Случайные события.
Основные определения. Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом.
Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу).
Случайными событиями (событиями), будем называть подмножества пространства элементарных событий W .
Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие w ц (или w 1), или гербом - элементарное событие w Г (или w 2). Соответствующее пространство элементарных событий W состоит из двух элементарных событий:
W = {w ц,w Г } или W = {w 1,w 2}.
Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w1, w 2, w 3, w 4, w 5, w 6}, где w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w4,w 6}, A![]() W .
W .
Пример 3. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий W = [0, 1] - множество действительных чисел на единичном отрезке.
В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.
Пространством элементарных событий называют произвольное множество W, W ={w}. Элементы w этого множества W называют элементарными событиями.
Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство W.
Событие W называется достоверным событием.
Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда.
Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е. W = {w 1, w 2, w 3, w 4, w 5, w 6}, где w i- выпадение i очков, - достоверное событие.
Невозможным событием называется пустое множество ![]() .
.
Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда.
Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда.
Пример 5. Бросаем один раз игральную кость. Выпадение более шести очков - невозможное событие ![]() .
.
Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Обозначается ![]() ,
, ![]() .
.
Пример 6. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, тогда событие ![]() - выпадение нечетного числа очков. Здесь W = {w 1, w 2, w 3,w 4, w 5,w 6}, где w i- выпадение i очков, A = {w 2,w 4,w 6},
- выпадение нечетного числа очков. Здесь W = {w 1, w 2, w 3,w 4, w 5,w 6}, где w i- выпадение i очков, A = {w 2,w 4,w 6}, ![]() =
= ![]() .
.
Несовместными событиями называются события A и B, для которых A B = ![]() .
.
Пример 7. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, событие B - выпадение числа очков, меньшего двух. Событие AB состоит в выпадении четного числа очков, меньшего двух. Это невозможно, A = {w 2,w 4,w 6}, B = {w 1}, AB = ![]() , т.е. события A и B - несовместны.
, т.е. события A и B - несовместны.
Действия со случайными событиями
Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.
Пример 8. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w1, w 2, w 3, w 4, w 5, w 6}, где элементарное событие w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}.
Событие A + B = {w 2,w 4, w 5, w 6} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B. Очевидно, что A + B ![]() W.
W.
Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.
Пример 9. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w1, w 2, w 3,w 4, w 5,w 6}, где элементарное событие w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}.
Событие A B состоит в том, что выпало четное число очков, большее четырех, т.е. произошли оба события, и событие A и событие B, A B = {w 6} A B ![]() W .
W .
Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.
Пример 10. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = {w 2,w 4,w6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}. Событие A\ B = {w 2,w 4} состоит в том, что выпало четное число очков, не превышающее четырех, т.е. произошло событие A и не произошло событие B, A\B ![]() W .
W .
Очевидно, что
A + A = A, AA = A, ![]()
![]() .
.
Нетрудно доказать равенства:
![]() , (A+B)C= AC + BC.
, (A+B)C= AC + BC.
Определения суммы и произведения событий переносятся на бесконечные последовательности событий:
![]() , событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из
, событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из![]() ;
;
![]() , событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем
, событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем ![]() .
.
Вероятность события. Аксиоматическое определение вероятности
Пусть W - произвольное пространство элементарных событий, а ![]() - такая совокупность случайных событий, для которой справедливо: W
- такая совокупность случайных событий, для которой справедливо: W ![]()
![]() , AB
, AB![]()
![]() , A+B
, A+B![]()
![]() и A\B
и A\B![]()
![]() , если A
, если A![]()
![]() и B
и B![]()
![]() .
.
Числовая функция P, определенная на совокупности событий ![]() , называется вероятностью, если:
, называется вероятностью, если:
-
P(A)
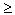 0 для любого A из
0 для любого A из .gif) ;
; -
P(W ) = 1;
-
если A
.gif)
.gif) и B
и B.gif)
.gif) несовместны, то P(A+B) = P(A) + P(B);
несовместны, то P(A+B) = P(A) + P(B); -
для любой убывающей последовательности событий {Ai}из
.gif) ,
,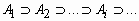 , такой, что
, такой, что 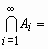
.gif) , имеет место равенство
, имеет место равенство 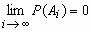 .
.
Тройку называют вероятностным пространством.
Вероятность события. Классическое определение вероятности
Пусть W= {w 1, w 2, …, w s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={w i1, w i2, …, w ik}, 1 ![]() i1
i1 ![]() i2
i2 ![]() …
… ![]() i k
i k![]() s, k = 1, 2,…, s, и пусть
s, k = 1, 2,…, s, и пусть ![]() . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество
. Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество ![]() состоит из всех подмножеств множества W :
состоит из всех подмножеств множества W : ![]() ). Таково классическое определение вероятности события A.
). Таково классическое определение вероятности события A.
Принята следующая формулировка классического определения вероятности: вероятностью события Aназывается отношение числа исходов, благоприятствующих A, к общему числу исходов.
Из приведенных определений следует: P(![]() )=0,
)=0, ![]() ,
, ![]() .
.
Вероятность суммы событий
Для любых двух событий A и B справедливо: ![]() .
.
Если события A и B несовместны, то ![]() .
.
Вероятность произведения событий. Условная вероятность. Независимые события
Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой
![]() .
.
Для любых двух событий A и B справедливо: ![]() .
.
События A и B называются независимыми, если ![]() . Для любых двух независимых, событий A и B справедливо:
. Для любых двух независимых, событий A и B справедливо: ![]() .
.
Формула полной вероятности. Формулы Байеса
Пусть A - произвольное событие, а события B1, B2, …, Bn - попарно несовместны и образуют полную группу событий, т.е. ![]() . Тогда имеет место следующая формула для вероятности события A - формула полной вероятности -
. Тогда имеет место следующая формула для вероятности события A - формула полной вероятности -
![]() , где P(Bk)>0, k=1, 2, …, n, A
, где P(Bk)>0, k=1, 2, …, n, A ![]() B1+ B2 + …+ Bn.
B1+ B2 + …+ Bn.
Если событие A произошло, то вероятность того, что имело место событие Bk
вычисляется по формуле Байеса: 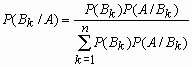 .
.
Случайные величины. Функции распределения, их свойства.
Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величина является одним из центральных понятий теории вероятностей.
Пусть ![]() - произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция x =x (w ), w
- произвольное вероятностное пространство. Случайной величиной называется действительная числовая функция x =x (w ), w ![]() W , такая, что при любом действительном x
W , такая, что при любом действительном x ![]() .
.
Событие ![]() принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x , h , z , …
принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x , h , z , …
Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямой I=[100, 3000]).
Функция распределения случайной величины. Её свойства
Каждая случайная величина полностью определяется своей функцией распределения.
Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
-
F(x) определена на всей числовой прямой R;
-
F(x) не убывает, т.е. если x1
.gif) x2, то F(x1)
x2, то F(x1).gif) F(x2);
F(x2); -
F(-
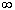 )=0, F(+
)=0, F(+.gif) )=1, т.е.
)=1, т.е. 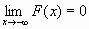 и
и 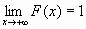 ;
; -
F(x) непрерывна справа, т.е.
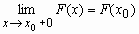
.
Функция распределения дискретной случайной величины
Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 <p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
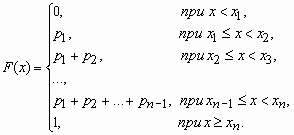
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
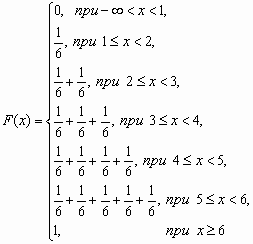
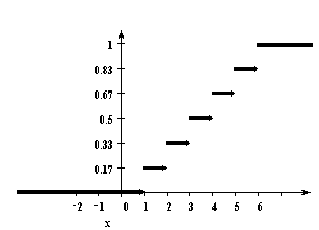
Функция распределения и плотность вероятности непрерывной случайной величины
Если функция распределения Fx (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулами
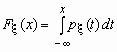 и
и ![]() .
.
Отсюда, в частности, следует, что для любой случайной величины 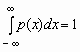 .
.
Квантили
При решении практических задач часто требуется найти значение x, при котором функция распределения Fx (x) случайной величины x принимает заданное значение p, т.е. требуется решить уравнение Fx (x) = p. Решения такого уравнения (соответствующие значения x) в теории вероятностей называются квантилями.
Квантилью xp (p-квантилью, квантилью уровня p) случайной величины ![]() , имеющей функцию распределения Fx (x), называют решение xp уравнения Fx (x) = p, p
, имеющей функцию распределения Fx (x), называют решение xp уравнения Fx (x) = p, p ![]() (0, 1). Для некоторых p уравнение Fx(x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.
(0, 1). Для некоторых p уравнение Fx(x) = p может иметь несколько решений, для некоторых - ни одного. Это означает, что для соответствующей случайной величины некоторые квантили определены неоднозначно, а некоторые кванитили не существуют.
Квантили, наиболее часто встречающиеся в практических задачах, имеют свои названия:
медиана - квантиль уровня 0.5;
нижняя квартиль - квантиль уровня 0.25;
верхняя квартиль - квантиль уровня 0.75;
децили - квантили уровней 0.1, 0.2, …, 0.9;
процентили - квантили уровней 0.01, 0.02, …, 0.99.
Вероятность попадания в интервал
Вероятность того, что значение случайной величины Fx (x) попадает в интервал (a, b), равная P(a < x < b) = Fx (b) -Fx (a), вычисляется по формулам:
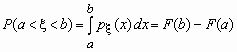 - для непрерывной случайной величины и
- для непрерывной случайной величины и
![]() - для дискретной случайной величины.
- для дискретной случайной величины.
Если a= - ![]() , то
, то ![]() ,
,
если b= ![]() , то
, то ![]() .
.
Числовые характеристики случайных величин.
Каждая случайная величина полностью определяется своей функцией распределения.
В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия.
Математическое ожидание случайной величины
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .
Математическое ожидание дискретной случайной величины x , имеющей распределение
| x1 | x2 | ... | xn |
| p1 | p2 | ... | pn |
называется величина ![]() , если число значений случайной величины конечно.
, если число значений случайной величины конечно.
Если число значений случайной величины счетно, то ![]() . При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.
. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.
Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле 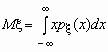 . При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.
. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.
Если случайная величина h является функцией случайной величины x , h = f(x), то
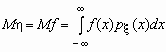 .
.
Аналогичные формулы справедливы для функций дискретной случайной величины:
![]() ,
, ![]() .
.
Основные свойства математического ожидания:
-
математическое ожидание константы равно этой константе, Mc=c ;
-
математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h );
-
математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).
Дисперсия случайной величины
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины xназывается величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
![]() ,
, 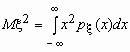 .
.
Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение ![]() , связанное с дисперсией соотношением
, связанное с дисперсией соотношением ![]() .
.
Основные свойства дисперсии:
-
дисперсия любой случайной величины неотрицательна, Dx
.gif) 0;
0; -
дисперсия константы равна нулю, Dc=0;
-
для произвольной константы D(cx ) = c2D(x );
-
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).
Моменты
В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные ицентральные моменты.
Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a k = Mx k.
Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx )k.
Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a 1 = Mx , а дисперсия - центральный момент второго порядка,
a 2 = Mx 2 = M(x - Mx )2 = Dx .
Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:
m 2=a 2-a 12, m 3 = a 3 - 3a 2a 1 + 2a 13.
Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.
Асимметрия
В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой 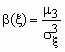 ,
,
где m 3 - центральный момент третьего порядка, ![]() - среднеквадратичное отклонение.
- среднеквадратичное отклонение.
Эксцесс
Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины x , от нормального распределения, является эксцесс.
Эксцесс g случайной величины x определяется равенством ![]() .
.
У нормального распределения, естественно, g = 0. Если g (x ) > 0, то это означает, что график плотности вероятностей px (x) сильнее “заострен”, чем у нормального распределения, если же g (x ) < 0, то “заостренность” графика px (x) меньше, чем у нормального распределения.
Среднее геометрическое и среднее гармоническое
Среднее гармоническое и среднее геометрическое случайной величины - числовые характеристики, используемые в экономических вычислениях.
Средним гармоническим случайной величины, принимающей положительные значения, называется величина 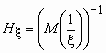 .
.
Например, для непрерывной случайной величины, распределенной равномерно на [a, b],
0 < a < b, среднее гармоническое вычисляется следующим образом:
![]() и
и 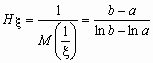 .
.
Средним геометрическим случайной величины, принимающей положительные значения, называется величина ![]() .
.
Название “среднее геометрическое” происходит от выражения среднего геометрического дискретной случайной величины, имеющей равномерное распределение
| x | a1 | a2 | a3 | ... | an |
| p | 1/n | 1/n | 1/n | ... | 1/n |
Среднее геометрическое, вычисляется следующим образом:
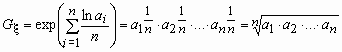 ,
,
т.е. получилось традиционное определение среднего геометрического чисел a1, a2, …, an.
Например, среднее геометрическое случайной величины, имеющей показательное распределение с параметром l , вычисляется следующим образом:
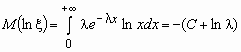 ,
, ![]() .
.
Здесь С » 0.577 - постоянная Эйлера.
Наиболее распространенные распределения дискретных случайных величин.
Биномиальное распределение
Пусть проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. С таким испытанием можно связать случайную величину x , значение которой равно числу успехов в серии из n испытаний. Эта величина принимает значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли
![]() , 0 < p <1, k = 0, 1, …, n,
, 0 < p <1, k = 0, 1, …, n, ![]() , Mx = np, Dx = npq,
, Mx = np, Dx = npq, ![]() .
.
Геометрическое распределение
Со схемой испытаний Бернулли можно связать еще одну случайную величину x - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до +![]() и ее распределение определяется формулой
и ее распределение определяется формулой
pk = P(x= k) = qk-1 p, 0 <p <1, k=1, 2, … , ![]() ,
, ![]() ,
, ![]() .
.
Гипергеометрическое распределение
В партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим x. Распределение такой случайной величины называется гипергеометрическим и имеет вид:
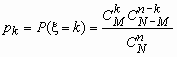 , k = 0, 1, …, min(n,M),
, k = 0, 1, …, min(n,M), 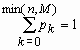 ,
,
![]() ,
, ![]() .
.
Пуассоновское распределение
Пуассоновское распределение c параметром l имеет случайная величина x , принимающая целые неотрицательные значения k = 0, 1, 2, … с вероятностями pk:
![]() ,
, ![]() , Mx =l, Dx = l , l > 0 - параметр распределения.
, Mx =l, Dx = l , l > 0 - параметр распределения.
Наиболее распространенные распределения непрерывных случайных величин.
Равномерное распределение
Непрерывная случайная величина x , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения px (x) и функция распределения Fx (x ) имеют соответственно вид:
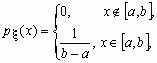
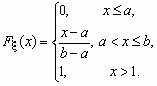
![]() ,
, ![]() .
.
Экспоненциальное (показательное) распределение
Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения px (x )и функция распределения Fx (x) имеют соответственно вид:
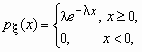
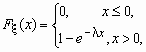
![]() ,
, ![]() .
.
Нормальное распределение
Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.
Случайная величина x нормально распределена с параметрами a и s , s >0, если ее плотность распределения px (x ) и функция распределения Fx (x) имеют соответственно вид:
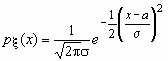 ,
, ![]() , Mx = a, Dx = s 2.
, Mx = a, Dx = s 2.
Часто используемая запись x ~ N(a, s ) означает, что случайная величина x имеет нормальное распределение с параметрами a и s .
Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N(0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:
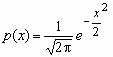 ,
, 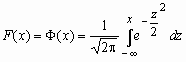 , Mx = 0, Dx = 1.
, Mx = 0, Dx = 1.
Здесь 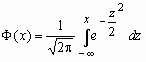 - функция Лапласа.
- функция Лапласа.
Функция распределения нормальной величины x ~ N(a, s ) выражается через функцию Лапласа следующим образом: ![]() .
.
Если x ~ N(a, s ), то случайную величину h = (x-a)/s называют стандартизованной или нормированной случайной величиной; h ~ N(0, 1) - имеет стандартное нормальное распределение.
Распределение хи-квадрат (c 2- распределение)
Пусть x 1, x 2, …, x n - независимые случайные величины, каждая из которых имеет стандартное нормальное распределение N(0, 1). Составим случайную величину
c 2 = x 12 + x 22 + …+ x n2.
Ее закон распределения называется c 2- распределением с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:
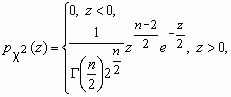
![]() , Dc 2=2n.
, Dc 2=2n.
Здесь 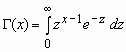 - гамма-функция Эйлера.
- гамма-функция Эйлера.
Распределение Стьюдента
Пусть случайная величина x имеет стандартное нормальное распределение, а случайная величина c n2 - c2-распределение с n степенями свободы. Если x и c n2 - независимы, то про случайную величину 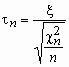 говорят, что она имеет распределение Стьюдента с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:
говорят, что она имеет распределение Стьюдента с nстепенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:
![]()
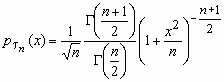 , x
, x ![]() R, Mt n = 0, Dt n = n/(n-2), n>2.
R, Mt n = 0, Dt n = n/(n-2), n>2.
При больших n распределение Стьюдента практически не отличается от N(0, 1).
F-распределение Фишера
Пусть случайные величины c n2и c m2 независимы и имеют распределение c 2 с n и mстепенями свободы соответственно. Тогда о случайной величине 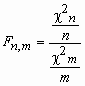 говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:
говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:
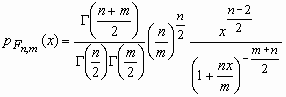 , x>0,
, x>0, 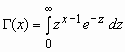 - гамма-функция Эйлера;
- гамма-функция Эйлера; ![]() , m>2;
, m>2; 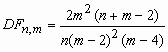 , m > 4.
, m > 4.
Распределение Парето
Распределение Парето часто применяется в экономических исследованиях. Плотность вероятностей для случайной величины, распределенной по Парето, имеет вид
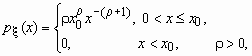
![]() ,
, ![]() .
.
Распределение Парето имеет математическое ожидание только при r > 1, а дисперсию - только при r > 2. Cлучайная величина, распределенная по Парето, принимает значения только в области x ![]() x0, x0 > 0.
x0, x0 > 0.
Логистическое распределение
Это еще одно распределение, широко применяемое в экономических исследованиях. Для случайной величины x , имеющей логистическое распределение, функция распределения и функция плотности вероятностей имеют соответственно вид:
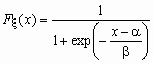 ,
, 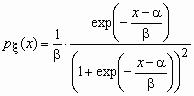 ,
,
![]() ,
, ![]() , x
, x ![]() R, a и b - параметры распределения.
R, a и b - параметры распределения.
По своим свойствам логистическое распределение очень похоже на нормальное.
Логнормальное распределение
Случайная величина x имеет логарифмическое нормальное (логнормальное) распределение с параметрами a и s , если случайная величина lnx имеет нормальное распределение с параметрами a >и s . Функция распределения и функция плотности вероятностей логнормального распределения имеют соответственно вид:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Бета-распределение
Случайная величина x имеет В-распределение (бета-распределение) с параметрами a1 и a2, если ее функция плотности вероятностей имеет вид:
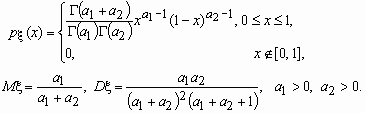
Распределение Вейбулла
Случайная величина x имеет распределение Вейбулла с параметрами l 0 и a , если ее функция распределения и функция плотности вероятностей имеют соответственно вид:
![]() ,
, 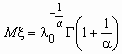 ,
, 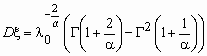 ,
, .gif) - гамма-функция Эйлера.
- гамма-функция Эйлера.
Распределение Коши
Случайная величина x имеет распределение Коши с параметрами a и c, если ее функция распределения и функция плотности вероятностей имеют соответственно вид:
![]()
У распределения Коши не существует ни математического ожидания, ни дисперсии. Это распределение не имеет ни одного момента положительного порядка.
Гамма-распределение
Случайная величина x имеет Г-распределение (гамма-распределение) с параметрами a и b, если ее функция плотности вероятностей имеет вид:
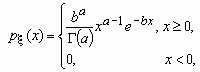 , a > 0, b > 0,
, a > 0, b > 0, ![]() ,
, ![]() ,
, 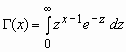 .
.
Распределение Лапласа
Случайная величина x имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром l , если ее функция плотности вероятностей имеет вид:
| , - | < x < | , Mx = 0, Dx = 2/l 2. |
Предельные теоремы для биномиального распределения.
Если число испытаний n в схеме независимых испытаний Бернулли растет, а вероятность p уменьшается, то точная формула ![]() практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).
практически непригодна из-за громоздких вычислений и возникающих погрешностей округления. В этом случае пользуются приближенными формулами Пуассона (при npq < 9) и Муавра-Лапласа (npq > 9).
Теорема Пуассона
Если число испытаний n в схеме независимых испытаний Бернулли стремится к бесконечности и ![]() так, что
так, что ![]() ,
, ![]() , то при любых
, то при любых ![]()
![]()
Это означает, что при больших n и малых p вместо громоздких вычислений по точной формуле ![]() можно воспользоваться приближенной формулой
можно воспользоваться приближенной формулой
![]() , т.е. использовать формулу Пуассона для l = np.
, т.е. использовать формулу Пуассона для l = np.
На практике пуассоновским приближением пользуются при npq < 9.
Локальная теорема Муавра-Лапласа
Пусть 0< p <1 и величина ![]() при n ®
при n ® ![]() ограничена. Тогда
ограничена. Тогда 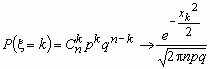 .
.
На практике приближением Муавра-Лапласа пользуются при npq > 9.
Точность формулы 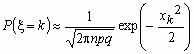 растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.
растет, как с ростом величин n и k, так и по мере приближения величин p и q к 0.5.
Интегральная теорема Муавра-Лапласа
Пусть 0< p <1, тогда для схемы Бернулли при n ® ![]() для любых a и b справедлива формула
для любых a и b справедлива формула
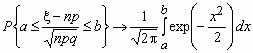 .
.
Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу
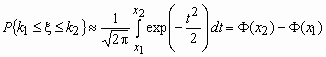 ,
,
где ![]() ,
, ![]() ,
, 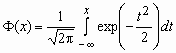 - функция Лапласа.
- функция Лапласа.
Точность этой приближенной формулы растет с ростом n.
Если npq сравнительно невелико, то лучшее приближение дает формула
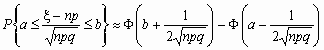
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2,можно использовать формулу
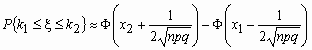 , где
, где ![]() ,
, ![]() .
.
Теорема Бернулли
Если x - число успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p, 0 < p < 1, то для любого e > 0 справедливо: ![]() .
.
Утверждение теоремы Бернулли означает, что с ростом числа испытаний n относительная частота успехов x /n приближается к вероятности p успеха в одном испытании.
Достаточно часто возникает необходимость установить, сколько нужно произвести испытаний, чтобы отклонение относительной частоты успехов x /n от вероятности p с вероятностью, больше или равной ![]() было меньше
было меньше ![]() . Т.е. требуется найти n, для которого справедливо неравенство
. Т.е. требуется найти n, для которого справедливо неравенство ![]() . Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению , где
. Доказано, что число n, которое обеспечивает выполнение этого неравенства, удовлетворяет соотношению , где ![]() - решение уравнения
- решение уравнения ![]() . Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!
. Следует обратить особое внимание на замечательный факт: искомое значение n не зависит от p!
Совместные распределения нескольких случайных величин.
В одном и том же случайном эксперименте можно рассматривать не одну, а несколько - n - числовых функций, определенных на одном и том же пространстве элементарных событий. Совокупность таких функций называется многомерной случайной величиной или случайным вектором и обозначается ![]() .
.
Точнее. На вероятностном пространстве ![]() заданы случайные величины
заданы случайные величины ![]() ; каждому w
; каждому w ![]() W эти величины ставят в соответствие n-мерный вектор
W эти величины ставят в соответствие n-мерный вектор ![]() , который называется n-мерным случайным вектором (n-мерной случайной величиной).
, который называется n-мерным случайным вектором (n-мерной случайной величиной).
Многомерные случайные величины. Функции распределения многомерных случайных величин.
Функцией распределения случайного вектора ![]() или совместным распределением случайных величин
или совместным распределением случайных величин ![]() называется функция, определенная равенством
называется функция, определенная равенством
![]() ,
,
где ![]() .
.
По известной многомерной функции ![]() можно найти распределение каждой из компонент
можно найти распределение каждой из компонент ![]() .
.
Например, если ![]() - двумерная случайная величина, имеющая совместное распределение
- двумерная случайная величина, имеющая совместное распределение ![]() , то распределения компонент
, то распределения компонент ![]() и
и ![]() вычисляются соответственно по формулам:
вычисляются соответственно по формулам:
![]() ,
, ![]() .
.
В дальнейшем будем рассматривать двумерные случайные векторы.
Случайный вектор ![]() называется непрерывным случайным вектором, если существует такая неотрицательная функция
называется непрерывным случайным вектором, если существует такая неотрицательная функция ![]() , что для любого прямоугольника W на плоскости
, что для любого прямоугольника W на плоскости ![]() вероятность события
вероятность события ![]() равна
равна
![]() .
.
Функция ![]() в этом случае называется совместной плотностью распределения.
в этом случае называется совместной плотностью распределения.
Легко показать, что ![]() .
.
Если ![]() - совместная плотность распределения двумерного случайного вектора
- совместная плотность распределения двумерного случайного вектора ![]() , то плотности распределения его компонент определяются равенствами:
, то плотности распределения его компонент определяются равенствами:
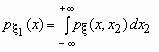 и
и 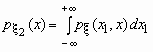 .
.
Если ![]() - дискретный случайный вектор, то совместным распределением случайных величин
- дискретный случайный вектор, то совместным распределением случайных величин ![]() и
и ![]() чаще всего называют таблицу вида
чаще всего называют таблицу вида
| y1 | y2 | ... | ym | |
| x1 | p11 | p12 | ... | p1m |
| x2 | p21 | p22 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
где ![]() и
и ![]() .
.
По этой таблице можно найти распределения ![]() и
и ![]() компонент x и h . Они вычисляются по формулам:
компонент x и h . Они вычисляются по формулам:
![]() .
.
Независимость случайных величин
Решить обратную задачу, т.е. восстановить совместное распределение (x , h ) по распределениям величин x и h , вообще говоря, невозможно. Однако эту задачу можно решить, когда случайные величины x и hнезависимы.
Случайные величины x и h называются независимыми, если для любых x1, x2 ![]() R2 справедливо равенство:
R2 справедливо равенство:
Fx ,h (x1, x2)= Fx (x1)Fh ( x2).
Для непрерывных случайных величин это определение эквивалентно следующему:
случайные величины называются независимыми, если
px ,h (x1, x2)= px (x1) ph (x2)
во всех точках непрерывности входящих в это равенство функций.
Для дискретных случайных величин x и h с матрицей совместного распределения {pij} условие независимости x и h имеет вид:
pij = P(x = xi, h = yj) = P(x = xi) P(h = yj),
для всех i = 1, 2, …, n, j = 1, 2, …, m.
Условные распределения случайных величин
Если две случайные величины x и h зависимы, то информация о том, какое значение на самом деле приняла одна из них, меняет наше представление о распределении другой. В связи с этим можно ввести понятие условного распределения.
Условные распределения дискретных случайных величин
Пусть дана двумерная случайная величина (x ,h ) с распределением
| y1 | y2 | ... | ym | |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
Тогда распределения случайных величин x и h имеют соответственно вид:
| x | x1 | x2 | ... | xn |
| p | p1· | p2· | ... | pn· |
| h | y1 | y2 | ... | yn |
| p· 1 | p· 2 | ... | p· n |
точка · в индексе означает суммирование по строкам или по столбцам:
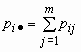 ,
, ![]() .
.
Условным распределением случайной величины ![]() при условии, что случайная величина
при условии, что случайная величина ![]() приняла значение
приняла значение ![]() , называется распределение:
, называется распределение:
| x | x1 | x2 | ... | xn |
| p | ... |
Нетрудно убедиться, что сумма вероятностей величины ![]() в этом распределении равна единице:
в этом распределении равна единице: 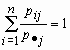 для всех j = 1, 2, …, m.
для всех j = 1, 2, …, m.
Совершенно аналогично условным распределением случайной величины ![]() при условии, что случайная величина
при условии, что случайная величина ![]() приняла значение
приняла значение ![]() , называется распределение:
, называется распределение:
| h | y1 | y2 | ... | yn |
| p | ... |
И 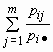 для всех i = 1, 2, …, n.
для всех i = 1, 2, …, n.
Если условные распределения случайных величин x и h отличаются от их безусловных распределений, то случайные величины x и h зависимы.
Условные распределения непрерывных случайных величин
Если ![]() - плотность вероятностей совместного распределения двумерной случайной величины
- плотность вероятностей совместного распределения двумерной случайной величины ![]() , то плотности вероятностей каждой ее компоненты вычисляются по формулам:
, то плотности вероятностей каждой ее компоненты вычисляются по формулам:
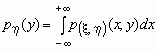 ,
, 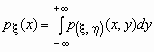 .
.
Условной плотностью распределения случайной величины x при условии, что случайная величина hпринимает значение h = y0, называется функция переменной x, определяемая формулой
![]() .
.
Аналогично, условной плотностью распределения случайной величины ![]() при условии, что случайная величина x принимает значение x = x0, называется функция переменной y, определяемая формулой
при условии, что случайная величина x принимает значение x = x0, называется функция переменной y, определяемая формулой
![]() .
.
Функции случайных величин.
Если x - случайная величина с областью значений Xx и функция f(x) определена на множестве Xx , то h = f(x) - тоже случайная величина. Задача об отыскании функции распределения случайной величины h по известной функции распределения случайной величины x легко решается, если f(x) - непрерывная монотонно возрастающая функция. Доказано, что тогда функция распределения Fh (x) случайной величины h задается формулой Fh (x)=Fx ([f(x)]-1).
Здесь Fx (x) - известная функция распределения случайной величины x , а символом [f(x)]-1 обозначена функция, обратная к функции f(x).
Плотность распределения случайной величины h для дифференцируемой f(x) вычисляется по формуле
![]() .
.
Плотность вероятности суммы двух случайных величин
В теории вероятностей часто возникает необходимость в определении плотности вероятности суммы двух независимых случайных величин. Если x 1 и x 2 - непрерывные независимые случайные величины с плотностями вероятности соответственно p1(x) и p2(x), то плотность вероятностей суммы h = x 1 + x 2вычисляется по формуле:
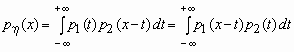 .
.
Распределение произведения двух случайных величин
Порядок построения распределения произведения двух дискретных случайных величин проще всего объяснить на примере.
Пусть (x , h ) - дискретный случайный вектор с распределением:
| 1 | 2 | 3 | 4 | |
| 0 | 0.01 | 0.02 | 0.03 | 0.04 |
| 1 | 0.1 | 0.1 | 0.2 | 0.4 |
| 2 | 0.05 | 0.01 | 0.01 | 0.03 |
Найдем распределение произведения случайных величин - случайной величины z = x * h,
которая принимает значения 0, 1, 2, 3, 4, 6, 8. Вычислим соответствующие вероятности:
P(z = x * h = 0) = P(x = 0, h = 1) + P(x = 0, h = 2) + P(x = 0, h = 3) + P(x = 0, h = 4) = 0.1;
P(z = 1) = P(x = 1, h = 1) =0.1; P(z = 2) = P(x = 1, h = 2) + P(x = 2, h = 1) =0.15; и т.д.
В результате получим распределение случайной величины z = x * h :
| 0 | 1 | 2 | 3 | 4 | 6 | 8 | |
| p | 0.1 | 0.1 | 0.15 | 0.2 | 0.41 | 0.01 | 0.03 |
Для того чтобы найти распределение произведения непрерывных случайных величин, необходимо выполнить более громоздкие вычисления.
Пусть (x , h ) - непрерывный двумерный случайный вектор с плотностью распределения p(x h )(x1, x2). Построим функцию распределения случайной величины z =x * h . Согласно определению
![]() .
.
Для вычисления этой вероятности рассмотрим отдельно случаи x>0 и x<0. Области интегрирования для обоих случаев на рисунке закрашены.
Область D={ x1x2 < x, x > 0} изображена на рисунке слева, а область D={ x1x2 < x, x < 0} - справа.
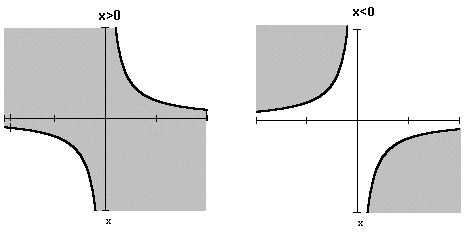
При x>0 имеем: 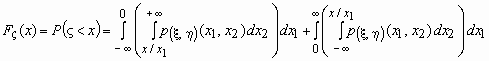 .
.
При x<0: 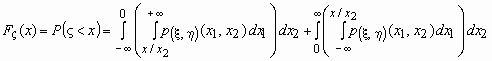 .
.
Числовые характеристики двумерных случайных величин.
В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай ![]() не вызывает затруднений.
не вызывает затруднений.
Математическое ожидание
Пусть (x , h ) - двумерная случайная величина, тогда M(x , h )=(M(x ), M(h )), т.е. математическое ожидание случайного вектора - это вектор из математических ожиданий компонент вектора.
Если (x , h ) - дискретный случайный вектор с распределением
| y1 | y2 | ... | ym | |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
то математические ожидания компонент вычисляются по формулам:
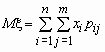 ,
, 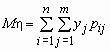 .
.
Эти формулы можно записать в сокращенном виде.
Обозначим 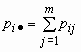 и
и ![]() , тогда
, тогда ![]() и
и 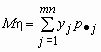 .
.
Если p(x , h )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины (x , h), то
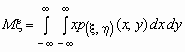 и
и 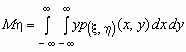 .
.
Поскольку 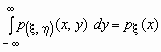 -плотность распределения случайной величины x , то
-плотность распределения случайной величины x , то 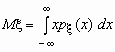 и, аналогично,
и, аналогично, 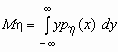 .
.
Дисперсия
Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.
Если (x , h ) - двумерная случайная величина, то
Dx = M(x - Mx )2 = Mx 2 - M(x )2, Dh = M(h - Mh )2 = Mh 2 - M(h )2.
Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.
Условное математическое ожидание
Между случайными величинами может существовать функциональная зависимость. Например, если x - случайная величина и h =x 2, то h - тоже случайная величина, связанная с x функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.
Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.
Для двумерного дискретного случайного вектора (x , h ) с распределением
| y1 | y2 | ... | ym | |
| x1 | p11 | p12 | ... | p1m |
| x2 | p12 | p12 | ... | p2m |
| ... | ... | ... | pij | ... |
| xn | pn1 | pn2 | ... | pnm |
условное математическое ожидание случайной величины x при условии, что случайная величина hпринимает значение yj, вычисляется по формуле 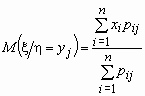 .
.
Аналогично, условное математическое ожидание случайной величины h при условии, что случайная величина x принимает значение xi, равно 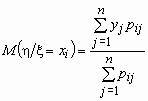 .
.
Видно, что условное математическое ожидание случайной величины x является функцией значений случайной величины h , т.е. M(x /h = y) = f1(y) и, совершенно аналогично, M(h /x = x) = f2(x).
Функцию f1(y) называют регрессией случайной величины x на случайную величину h , а f2(x) - регрессией случайной величины h на случайную величину x .
Если p(x ,h )(x, y) совместная плотность вероятностей двумерной случайной величины (x ,h ), то
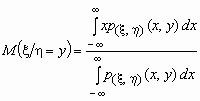 и
и 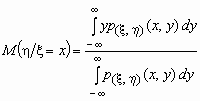 .
.
Ковариация
Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov(x , h ). Ковариацию вычисляют по формулам cov(x , h )=M[(x - Mx )(h - Mh )] = M(x h) - Mx Mh .
Если случайные величины x и h независимы, то cov(x ,h )=0.
Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.
Свойства ковариации:
cov(x , x ) = Dx ;
![]() ;
;
![]() ;
;
![]() ,
,
где C1 и C2 - произвольные константы.
Ковариационной матрицей случайного вектора (x ,h ) называется матрица вида
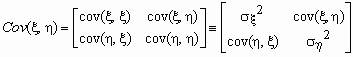 .
.
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин (x ,h ).
Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: ![]() . Если же случайные величины зависимы, то
. Если же случайные величины зависимы, то ![]() .
.
Корреляция
Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции ![]() .
.
Этот коэффициент обладает следующими свойствами:
он безразмерен;
его модуль не превосходит единицы, т.е. ![]() ;
;
если x и h независимы, то k(x ,h )=0 (обратное неверно!);
если ![]() , то случайные величины x и h связаны функциональной зависимостью вида
, то случайные величины x и h связаны функциональной зависимостью вида
h = ax +b,
где a и b- некоторые числовые коэффициенты;
![]() ;
;
Корреляционной матрицей случайного вектора называется матрица
![]() .
.
Если ![]() и
и ![]() , то ковариационная и корреляционная матрицы случайного вектора (x ,h ) связаны соотношением
, то ковариационная и корреляционная матрицы случайного вектора (x ,h ) связаны соотношением ![]() , где
, где ![]() .
.
Закон больших чисел.
Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений.
Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Названием "закон больших чисел" объединена группа теорем, устанавливающих устойчивость средних результатов большого количества случайных явлений и объясняющих причину этой устойчивости.
Простейшая форма закона больших чисел, и исторически первая теорема этого раздела - теорема Бернулли, утверждающая, что если вероятность события одинакова во всех испытаниях, то с увеличением числа испытаний частота события стремится к вероятности события и перестает быть случайной.
Теорема Пуассона утверждает, что частота события в серии независимых испытаний стремится к среднему арифметическому его вероятностей и перестает быть случайной.
Предельные теоремы теории вероятностей, теоремы Муавра-Лапласа объясняют природу устойчивости частоты появлений события. Природа эта состоит в том, что предельным распределением числа появлений события при неограниченном возрастании числа испытаний (если вероятность события во всех испытаниях одинакова) является нормальное распределение.
Центральная предельная теорема объясняет широкое распространение нормального законараспределения. Теорема утверждает, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин с конечными дисперсиями, закон распределения этой случайной величины оказывается практически нормальным законом.
Теорема, приведенная ниже под названием "Закон больших чисел" утверждает, что при определенных, достаточно общих, условиях, с увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным.
Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения.
В основе качественных и количественных утверждений закона больших чисел лежит неравенство Чебышева. Оно определяет верхнюю границу вероятности того, что отклонение значения случайной величины от ее математического ожидания больше некоторого заданного числа. Замечательно, что неравенство Чебышева дает оценку вероятности события ![]() для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.
для случайной величины, распределение которой неизвестно, известны лишь ее математическое ожидание и дисперсия.
Неравенство Чебышева. Если случайная величина x имеет дисперсию, то для любого e > 0 справедливо неравенство ![]() , где Mx и Dx - математическое ожидание и дисперсия случайной величины x .
, где Mx и Dx - математическое ожидание и дисперсия случайной величины x .
Теорема Бернулли. Пусть m n - число успехов в n испытаниях Бернулли и p - вероятность успеха в отдельном испытании. Тогда при любом e > 0 справедливо ![]() .
.
Центральная предельная теорема. Если случайные величины x 1, x 2, …, x n, … попарно независимы, одинаково распределены и имеют конечную дисперсию, то при n ® ![]() равномерно по x
равномерно по x ![]() (-
(-![]() ,
,![]() )
)
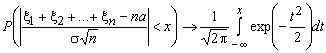 .
.
Закон больших чисел. Если случайные величины x 1, x 2, …, x n, … попарно независимы и![]() ,то для любого e > 0
,то для любого e > 0
![]() .
.
Теорема Ляпунова. Пусть x 1, x 2, …, x n, …- неограниченная последовательность независимых случайных величин с математическими ожиданиями m1, m2, …, mn, … и дисперсиями s 12, s 22, …, s n2… . Обозначим ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Тогда ![]() = Ф(b) - Ф(a) для любых действительных чисел a и b , где Ф(x) - функция распределения нормального закона.
= Ф(b) - Ф(a) для любых действительных чисел a и b , где Ф(x) - функция распределения нормального закона.
Основные инструменты Mathcad для решения задач теории вероятностей.
Дискретная случайная величина ![]() с вероятностями
с вероятностями ![]() может быть задана распределением - таблицей вида
может быть задана распределением - таблицей вида
| ... | ... | ||||
| ... | ... |
Такие таблицы в среде Mathcad удобно хранить в виде матрицы размерности ![]() .
.
Функция распределения случайной величины, имеющей приведенное выше распределение, имеет вид
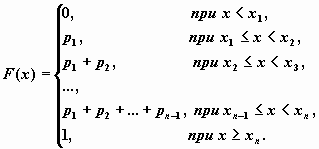
В приведенном ниже примере показано, как в Mathcad можно определить дискретную случайную величину, ее функцию распределения и построить график функции распределения.
ПРИМЕР 1. Определим случайную величину, заданную приведенным ниже распределением. Определим в Mathcad эту случайную величину, определим ее функцию распределения и построим график функции распределения. Дискретная случайная величина имеет распределение
| 1 | 0 | 7 | 4 | -2 | |
Распределение дискретного случайного вектора
Распределение дискретного случайного вектора ![]()
| ... | ||||
| ... | ||||
| ... | ||||
| ... | ... | ... | ... | ... |
| ... |
также удобно хранить в матрице размерности ![]() . Первому элементу первой строки этой матрицы присваивается нулевое значение, остальные элементы первой строки содержат значения случайной компоненты
. Первому элементу первой строки этой матрицы присваивается нулевое значение, остальные элементы первой строки содержат значения случайной компоненты ![]() , элементы первого столбца - значения случайной компоненты
, элементы первого столбца - значения случайной компоненты ![]() , а остальные элементы - соответствующие вероятности: элемент, расположенный в
, а остальные элементы - соответствующие вероятности: элемент, расположенный в ![]() -м столбце
-м столбце ![]() -й строки содержит значение вероятности
-й строки содержит значение вероятности ![]() того, что случайный вектор
того, что случайный вектор ![]() принимает значение
принимает значение ![]() .
.
В приведенном ниже примере показано, как в Mathcad можно определить двумерный случайный вектор.
ПРИМЕР 2. Определим в Mathcad двумерный случайный вектор. Случайный вектор задан следующей таблицей:
| 1 | 3 | 5 | 7 | |
| 2 | 0.01 | 0.01 | 0.17 | 0.01 |
| 4 | 0.1 | 0.2 | 0.1 | 0.2 |
| 6 | 0.02 | 0.05 | 0.09 | 0.04 |
Библиотека стандартных распределений
Для вычислений со случайными величинами (непрерывными и дискретными) в Mathcad есть богатая библиотека встроенных функций наиболее распространенных стандартных распределений. Каждое распределение представлено в библиотеке тремя функциями - плотностью вероятностей для непрерывных распределений и функцией, вычисляющей вероятность заданного значения - для дискретных распределений, функцией распределения и функцией, обратной к функции распределения.
Например, для нормального распределения - это функции ![]() ,
, ![]() и
и ![]() . Значением функции
. Значением функции ![]() является значение в точке
является значение в точке ![]() плотности вероятностей случайной величины
плотности вероятностей случайной величины ![]() , имеющей нормальное распределение с математическим ожиданием
, имеющей нормальное распределение с математическим ожиданием ![]() и дисперсией
и дисперсией ![]() ; значение функции
; значение функции ![]() - значение функции распределения этой же случайной величины
- значение функции распределения этой же случайной величины ![]() ; значением функции
; значением функции ![]() является решение уравнения
является решение уравнения ![]() , где
, где ![]() - функция распределения, определенная функцией
- функция распределения, определенная функцией ![]() , т.е. значением
, т.е. значением ![]() является квантиль уровня
является квантиль уровня ![]() нормально распределенной случайной величины. Имена всех встроенных функций, определяющих плотности вероятностей, начинаются с буквы
нормально распределенной случайной величины. Имена всех встроенных функций, определяющих плотности вероятностей, начинаются с буквы ![]() , определяющих функции распределения - с буквы
, определяющих функции распределения - с буквы ![]() , определяющих квантили - с буквы
, определяющих квантили - с буквы ![]() .
.
Ниже приведен список всех распределений, представленных в библиотеке Mathcad, и имена соответствующих функций:
бета-распределение - ![]() ,
, ![]() ,
, ![]() ;
;
биномиальное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
распределение Коши- ![]() ,
, ![]() ,
,![]() ;
;
![]() -распределение-
-распределение- ![]() ,
, ![]() ,
, ![]() ;
;
экспоненциальное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
распределение Фишера, F-распределение - ![]() ,
, ![]() ,
, ![]() ;
;
Гамма-распределение - ![]() ,
, ![]() ,
, ![]() ;
;
геометрическое распределение - ![]() ,
, ![]() ,
, ![]() ;
;
логнормальное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
логистическое распределение - ![]() ,
, ![]() ,
, ![]() ;
;
отрицательное биномиальное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
нормальное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
распределение Пуассона - ![]() ,
, ![]() ,
, ![]() ;
;
распределение Стьюдента - ![]() ,
, ![]() ,
, ![]() ;
;
равномерное распределение - ![]() ,
, ![]() ,
, ![]() ;
;
распределение Вейбулла - ![]() ,
, ![]() ,
, ![]() .
.
В приведенном ниже примере построены графики и выполнены вычисления, демонстрирующие некоторые основные свойства функций, связанных со стандартным нормальным распределением ![]() .
.
ПРИМЕР 3. Построим график плотности вероятностей и функции распределения для стандартного нормального распределения. Вычислим квантиль a уровня 0.1 и значение функции распределения в точке x = a (т.е. проверим правильность вычисления квантили).
Кроме перечисленных функций, в библиотеке встроенных функций Mathcad есть функция Лапласа (интеграл ошибок) 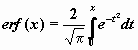 .
.
Для вычисления числовых характеристик дискретных и непрерывных случайных величин в Mathcad есть операторы интегрирования и дифференцирования вычисления конечных сумм и суммирования рядов, которые могут быть выполнены щелчком мыши по кнопке в панели ![]() и заполнением соответствующих помеченных полей.
и заполнением соответствующих помеченных полей.
Примеры
Пример 1.
Определим случайную величину, заданную приведенным ниже распределением. Определим в Mathcad эту случайную величину, определим ее функцию распределения и построим график функции распределения. Дискретная случайная величина имеет распределение
![]()
Решение примера с MATLAB:
% Определить случайную величину, заданную дискретным распределением
% Построить график функции распределения
% Значения случайной величины
val = [-2 0 1 4 7];
% Распределение вероятностей
prob = [0.2 0.5 0.1 0.1 0.1];
% Получить значения дискретной функции распределения
f = cumsum(prob);
% Нарисовать её график
stairs(val, f);
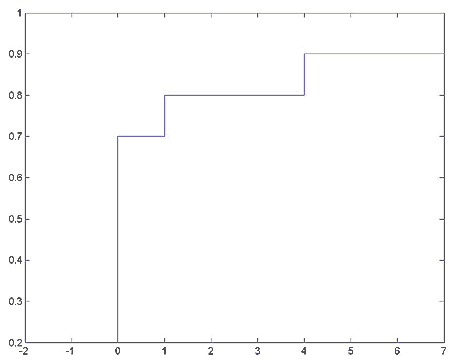
Пример 2.
Определим в математическом пакете двумерный случайный вектор.
Решение примера с MATLAB:
Определить двумерный случайный вектор.
Определим двумерный случайный вектор
![[Graphics:Images/index_gr_1.gif]](https://exponenta.ru/storage/app/media/hub_exponenta_publications/kurs-po-teorii-veroyatnostey835/index_gr_1.gif)
Здесь элементы первой строки с второго по последний означают значения первой компоненты вектора, элементы первого столбца с второго по последний означают значения второй компоненты вектора, а остальные элементы - соответствующие вероятности.
![]()
Пример 3.
Построим график плотности вероятностей и функции распределения для стандартного нормального распределения. Вычислим квантиль a уровня 0.1 и значение функции распределения в точке x = a (т.е. проверим правильность вычисления квантили).
Решение примера с MATLAB:
% Построить график функции распределения и плотности стандартного нормального распределения.
% Вычислить квантили и значение функции распределения в точке
% Строим на отрезке [-3,3]
x = -3:0.01:3;
% Соотношение между erf и стандартным нормальным распределением
distr = (1 + (erf(x/sqrt(2))))./2;
% Требуется нарисовать несколько графиков на одних осях
axes('NextPlot', 'add');
% График функции распределения.
% Её производная - плотность
plot(x, distr, x, gradient(distr, 0.01));
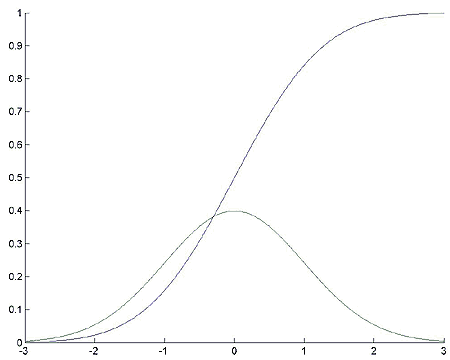
Комментарии