| Нули
аналитической функции. Найти нули функции f(z) =
ch(z)+1 и определить их порядок |
|
Определим
функцию и найдем ее нули - корни уравнения f(z)=0: |
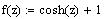 |
Для
того чтобы определить функцию, введите ее имя,
имя аргумента в скобках, знак присваивания
(одновременно клавиши <Shift> и <=>) и выражение
для вычисления функции |
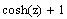 |
Для
того чтобы найти корни уравнения f(z)=0, введите
выражение для вычисления функции, выделите
рамкой переменную z, затем выберите в меню Symbolic роцедуры Variable - Solve |
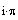 |
|
| Нуль
функции - z=ip |
|
|
Найдем
производную f'(z) и вычислим ее значение в точке z=ip |
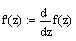
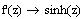 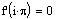 |
Для
того чтобы ввести мнимую единицу i, наберите на
клавиатуре 1i и щелкните мышью вне выделяющей
рамки |
|
|
Найдем
вторую производную f''(z) и вычислим ее значение в
точке z=ip |
Из того,
что f(ip)=f'(ip)=0, а вторая
производная f''(ip)=
-1 отлична от нуля, делаем вывод, что точка z = ip является
нулем второго порядка.
А поскольку f(z) = 1+ch(z) - периодическая функция с
периодом 2pi,
то она имеет бесконечное множество нулей второго
порядка:
точки zk = ip + 2kp являются
нулями второго порядка функции f(z) = 1+ch(z)