наберите на клавиатуре 1i и
щелкните мышью вне выделяющей рамки
| Различные формы представления комплексных чисел. Способы определения комплексного числа | |
| Комплексные числа в алгебраической форме. Первый способ: | |
| Для
того чтобы ввести мнимую единицу i, наберите на клавиатуре 1i и щелкните мышью вне выделяющей рамки |
|||
| Для того чтобы отобразить комплексное число в рабочем документе в алгебраической форме, щелкните в панели Symbolic по ключевому слову complex и введите в помеченной позиции имя комплексной переменной и щелкните мышью вне выделяющей рамки | |||
| Комплексные числа в алгебраической форме. Второй способ: |
| Комплексные числа в алгебраической форме. Третий способ: |
| Комплексные числа в тригонометрической форме. |
| Комплексные числа в показательной форме. |
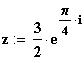 |
| Действительная и мнимая части комплексного числа |
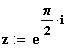 |
|||
| Модуль и аргумент комплексного числа |
| Для того чтобы найти модуль комплексного числа, щелкните в панели Calculator по символу модуля и введите в помеченной позиции имя числа | |||
| Для того чтобы найти аргумент комплексного числа, введите имя функции arg и укажите в скобках комплексное число (или его имя) | |||
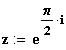 |
|||
| Вычисление комплексно сопряженного числа |
| Для того чтобы определить комплексно сопряженное к числу z, введите с клавиатуры z и затем символ " (кавычки) | ||
| Изображение комплексных чисел на комплексной плоскости |
| Комплексные числа a, b и d определены выше: | ||
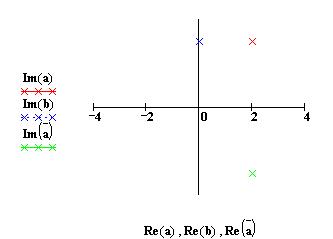 |
Для того
чтобы отобразить комплексное число на
комплексной плоскости,щелкните в панели Graph по
символу декартова графика, в открывшемся окне
графиков введите в помеченной позиции возле оси
абсцисс, разделяя запятой, имена действительных
частей комплексных чисел, а в позиции возле оси
ординат - имена мнимых частей, и щелкните вне поля
графиков. Для того чтобы устанвить стиль изображения, щелкните по графику дважды и посмотрите метки в полях ввода, чтобы понять, как определен стиль изображения для приведенного графика. |
|