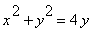 ,
,
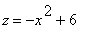 ,
,
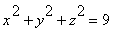 ,
,
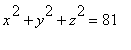 ,
,
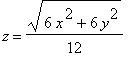 ,
,
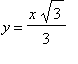 .
.
Замена переменных в кратных интегралах
Вычисление якобиана для цилиндрических и сферических координат. Вычислим объем тела, ограниченного поверхностями
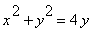 ,
,
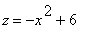 ,
,
![]() . То же для тела, ограниченного поверхностями
. То же для тела, ограниченного поверхностями
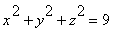 ,
,
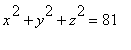 ,
,
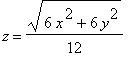 ,
,
![]() ,
,
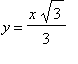 .
.
| > | restart; |
Цилиндрические координаты.
| > | x:=r*cos(t);y:=r*sin(t);z:=z; |
![]()
![]()
![]()
Вычислим якобиан.
| > | with(LinearAlgebra): |
| > | M:=Matrix([[diff(x,r),diff(x,t),diff(x,z)],[diff(y,r),diff(y,t),diff(y,z)],[diff(z,r),diff(z,t),diff(z,z)]]); |
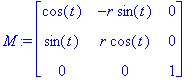
| > | J:=Determinant(M); |
![]()
| > | simplify(J,trig); |
![]()
Сферические координаты.
| > | x:=r*sin(t)*cos(phi);y:=r*sin(t)*sin(phi);z:=r*cos(t); |
![]()
![]()
![]()
Вычислим якобиан.
| > | M:=Matrix([[diff(x,r),diff(x,t),diff(x,phi)],[diff(y,r),diff(y,t),diff(y,phi)],[diff(z,r),diff(z,t),diff(z,phi)]]); |
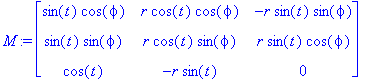
| > | J:=Determinant(M); |
![]()
| > | simplify(J,trig); |
![]()
Для вычисления якобианов можно использовать функцию Jacobian пакета VectorCalculus.
| > | restart; |
| > | with(VectorCalculus): |
Warning, the assigned names <,> and <|> now have a global binding
Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series
Цилиндрические координаты.
| > | (M,d):=Jacobian( [r*cos(t),r*sin(t),z], [r,t,z], 'determinant' ); |
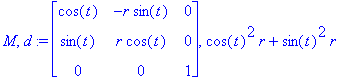
| > | simplify(d,trig); |
![]()
Сферические координаты.
| > | (M,d):=Jacobian( [r*sin(t)*cos(phi),r*sin(t)*sin(phi),r*cos(t)], [r,t,phi], 'determinant' ); |
![]()
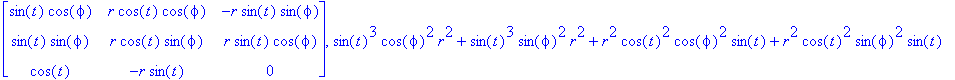
| > | simplify(d,trig); |
![]()
Вычислим объем первого тела.
| > | restart; |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | S:={x^2+y^2-4*y=0, z-6+x^2=0, z=0}; |
![]()
Нарисуем заданные поверхности.
| > | implicitplot3d(S,x=-2..2,y=-1..5,z=0..6); |
![[Maple Plot]](images/ex227.gif)
Произведем сдвиг системы координат по оси y .
| > | y:=v+2; |
![]()
В новой системе координат уравнения, задающие тело, имеют более простой вид.
| > | simplify(S); |
![]()
Объем тела можно посчитать по формуле
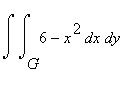 , где G - круг
, где G - круг
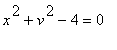 .
.
Перейдем к полярным координатам. Тогда интеграл можно переписать в виде повторного.
| > | V:=Int(Int((6-r^2*(cos(t))^2)*abs(r),r=0..2),t=0..2*Pi); |
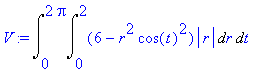
| > | V:=value(%); |
![]()
Вычислим объем второго тела.
| > | restart; |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | S:={x^2+y^2+z^2-9=0,x^2+y^2+z^2-81=0,z=0,z-sqrt((x^2+y^2)/24)=0,y=0,y-x/sqrt(3)=0}; |
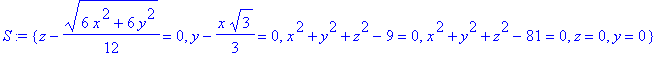
Нарисуем заданные поверхности.
| > | implicitplot3d(S,x=-10..10,y=0..10,z=0..6); |
![[Maple Plot]](images/ex235.gif)
Перейдем к сферическим координатам.
| > | x:=r*sin(t)*cos(phi);y:=r*sin(t)*sin(phi);z:=r*cos(t); |
![]()
![]()
![]()
| > | simplify(S,symbolic); |
![]()
Интеграл сводится к виду:
| > | V:=Int(Int(Int(r^2*sin(t),r=3..9),t=arccot(1/(2*sqrt(6)))..Pi/2),phi=0..Pi/6); |
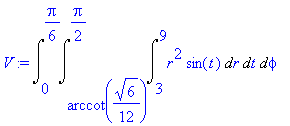
| > | V:=value(%); |
![]()