Курс по математическому анализу
Вашему вниманию предлагается курс по математическому анализу.
Содержание
-
4. Бесконечно малые функции. Сравнение бесконечно малых функций.
-
15. Неопределенный интеграл, простейшие методы интегрирования.
-
18. Применение определенного интеграла для площадей и длин дуг.
1. Предел числовой последовательности.
Последовательность ![]() - это функция, заданная на множестве натуральных чисел
- это функция, заданная на множестве натуральных чисел ![]() . Число
. Число ![]() называется пределом последовательности
называется пределом последовательности ![]() , если для любого положительного числа
, если для любого положительного числа ![]() , как бы мало оно ни было, существует такой номер
, как бы мало оно ни было, существует такой номер![]() , что для всех
, что для всех ![]() c номерами
c номерами ![]() справедливо неравенство
справедливо неравенство ![]() . Неравенство
. Неравенство ![]() , эквивалентное неравенству
, эквивалентное неравенству![]() , означает, что для любого
, означает, что для любого![]() существует такой номер
существует такой номер![]() , что все
, что все ![]() c номерами
c номерами![]() расположены между
расположены между ![]() и
и ![]() . Последовательность, предел которой - конечное число
. Последовательность, предел которой - конечное число ![]() , называется сходящейся, и ее предел обозначают
, называется сходящейся, и ее предел обозначают![]() . Если изобразить элементы последовательности
. Если изобразить элементы последовательности![]() на плоскости точками с координатами
на плоскости точками с координатами ![]() , то неравенства
, то неравенства ![]() означают, что все точки
означают, что все точки ![]() с номерами
с номерами![]() расположены между параллельными оси абсцисс прямыми
расположены между параллельными оси абсцисс прямыми![]() и
и![]() .
.
Бесконечно малая последовательность. Последовательность ![]() , предел которой равен нулю
, предел которой равен нулю ![]() , называется бесконечно малой.
, называется бесконечно малой.
Бесконечно большая последовательность. Последовательность ![]() называется бесконечно большой, если для любого положительного числа
называется бесконечно большой, если для любого положительного числа ![]() , как бы велико оно ни было, существует такой номер
, как бы велико оно ни было, существует такой номер ![]() , что для всех
, что для всех ![]() с номерами
с номерами![]() справедливо неравенство
справедливо неравенство ![]() , записываем
, записываем ![]() .
.
2. Методы вычисления пределов последовательностей.
Пусть заданы две последовательности ![]() и
и ![]() . Если существуют
. Если существуют ![]() и
и ![]() , то существуют и пределы суммы и произведения последовательностей, а при
, то существуют и пределы суммы и произведения последовательностей, а при ![]() и предел частного, причем
и предел частного, причем ![]() ,
, ![]() ,
, 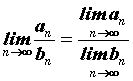 . Для правильного применения этих теорем очень важно существование пределов каждой последовательности.
. Для правильного применения этих теорем очень важно существование пределов каждой последовательности.
Неопределенности и их раскрытие.
Если ![]() и
и ![]() , то может существовать
, то может существовать ![]() . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа ![]() . Также может существовать
. Также может существовать 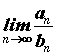 , в этом случае имеем неопределенность типа
, в этом случае имеем неопределенность типа ![]() . Если
. Если ![]() и
и ![]() , то может существовать
, то может существовать.gif) . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа ![]() . Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.
. Поскольку в перечисленных случаях не применимы теоремы о пределе суммы, произведения и частного, используют другие способы вычисления, которые называют методами раскрытия неопределенностей. Это, как правило, алгебраические преобразования, приводящие выражения к виду, при котором можно пользоваться упомянутыми теоремами.
3. Предел функции в точке.
Рассмотрим функцию ![]() , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки ![]() ,
, ![]() ,
,![]() , за исключением, быть может, самой точки
, за исключением, быть может, самой точки ![]() . Число
. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , стремящемся к
, стремящемся к ![]() , если для любого положительного числа
, если для любого положительного числа ![]() , как бы мало оно ни было, существует такое положительное число
, как бы мало оно ни было, существует такое положительное число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , справедливо неравенство
, справедливо неравенство ![]() . Говорят “предел функции
. Говорят “предел функции ![]() в точке
в точке ![]() ” и обозначают
” и обозначают ![]() . Неравенство
. Неравенство ![]() для всех
для всех ![]() , эквивалентное неравенствам
, эквивалентное неравенствам ![]() ,
, ![]() , означают, что для любого
, означают, что для любого ![]() существует такое
существует такое ![]() , что для
, что для ![]() график функции
график функции ![]() расположен на плоскости
расположен на плоскости ![]() в прямоугольнике
в прямоугольнике ![]() . При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно:
. При вычислениях на компьютере мы имеем дело с дискретными значениями переменных. Поэтому удобнее пользоваться другим, эквивалентным приведенному, определением предела. А именно: ![]() , если для любой, сходящейся к
, если для любой, сходящейся к ![]() последовательности значений аргумента
последовательности значений аргумента ![]() , соответствующая последовательность значений функции
, соответствующая последовательность значений функции ![]() сходится к числу
сходится к числу ![]() . Отсюда следует, в частности, что для любого
. Отсюда следует, в частности, что для любого ![]() существует такое
существует такое ![]() , что для любой последовательности
, что для любой последовательности ![]() , сходящейся к
, сходящейся к ![]() , точки с координатами
, точки с координатами ![]() находятся на плоскости внутри прямоугольника
находятся на плоскости внутри прямоугольника ![]() .
.
Бесконечно большие функции.
Если для любой последовательности ![]() значений аргумента соответствующая последовательность значений функции
значений аргумента соответствующая последовательность значений функции![]() бесконечно большая, то функция
бесконечно большая, то функция ![]() называется бесконечно большой в точке
называется бесконечно большой в точке ![]() . Если
. Если ![]() бесконечно большая в точке
бесконечно большая в точке ![]() , то для любого положительного числа
, то для любого положительного числа ![]() , как бы велико оно ни было, существует такое число
, как бы велико оно ни было, существует такое число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , справедливо неравенство
, справедливо неравенство ![]() ; обозначают
; обозначают ![]() .
.
4. Бесконечно малые функции. Сравнение бесконечно малых функций.
Рассмотрим функцию![]() , определенную в некоторой окрестности
, определенную в некоторой окрестности ![]() точки
точки ![]() ,
, ![]() , за исключением, быть может, самой точки
, за исключением, быть может, самой точки ![]() . Функция
. Функция ![]() называется бесконечно малой при
называется бесконечно малой при ![]() , стремящемся к
, стремящемся к ![]() , если
, если ![]() . Если
. Если ![]() — бесконечно малая в точке
— бесконечно малая в точке ![]() , то для любого положительного числа
, то для любого положительного числа ![]() , как бы мало оно ни было, существует такое положительное число
, как бы мало оно ни было, существует такое положительное число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству![]() , справедливо неравенство
, справедливо неравенство ![]() . Неравенства
. Неравенства ![]() для всех
для всех ![]() , эквивалентные неравенствам
, эквивалентные неравенствам ![]() ,
, ![]() , означают, что для любого
, означают, что для любого ![]() существует такое
существует такое ![]() , что для
, что для ![]() график функции расположен на плоскости в прямоугольнике
график функции расположен на плоскости в прямоугольнике ![]() . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию
. Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию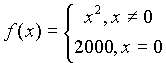 . При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.
. При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.
Сравнение бесконечно малых функций.
Пусть ![]() и
и ![]() — две функции, бесконечно малые в точке
— две функции, бесконечно малые в точке ![]() . Если
. Если 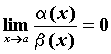 , то говорят, что
, то говорят, что ![]() более высокого порядка малости, чем
более высокого порядка малости, чем ![]() и обозначают
и обозначают ![]() . Если же
. Если же 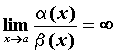 , то
, то ![]() более высокого порядка малости, чем
более высокого порядка малости, чем![]() ; обозначают
; обозначают ![]() . Бесконечно малые функции
. Бесконечно малые функции ![]() и
и ![]() называются бесконечно малыми одного порядка малости, если
называются бесконечно малыми одного порядка малости, если 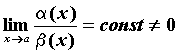 , обозначают
, обозначают ![]() . И, наконец, если
. И, наконец, если 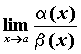 не существует, то бесконечно малые функции
не существует, то бесконечно малые функции ![]() и
и ![]() несравнимы.
несравнимы.
Эквивалентные бесконечно малые функции.
Если 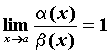 , то бесконечно малые функции
, то бесконечно малые функции ![]() и
и ![]() называются эквивалентными, обозначают
называются эквивалентными, обозначают![]() ~
~![]() .
.
5. Методы вычисления пределов функций.
Пусть заданы две функции![]() и
и ![]() . Если существуют
. Если существуют ![]() и
и ![]() , то существуют и пределы суммы и произведения этих функций, а при
, то существуют и пределы суммы и произведения этих функций, а при ![]() и предел частного, причем
и предел частного, причем
![]() ,
,
![]() ,
,
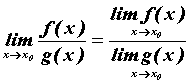 .
.
Для правильного применения этих теорем очень важно существование пределов каждой функции. Не трудно доказать, что предел постоянной функции равен этой постоянной, то есть ![]() . Из приведенных формул следует полезное утверждение:
. Из приведенных формул следует полезное утверждение:
![]() , то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной
, то есть постоянный множитель можно выносить за знак предела. Если сделать замену переменной ![]() , то вычисление предела при
, то вычисление предела при ![]() всегда можно свести к вычислению предела при
всегда можно свести к вычислению предела при![]() . Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке
. Из определения непрерывной функции следует, что ее предел совпадает со значением функции в этой точке. Доказывают, что все элементарные функции непрерывны в области определения, поэтому, если функция определена, то вычисление предела сводится к применению указанных теорем и подстановке ![]() в выражение для функции.
в выражение для функции.
Неопределенности и их раскрытие.
Существуют случаи, когда не применимы теоремы о пределах суммы, произведения, частного, но предел существует и может быть вычислен. Если ![]() и
и ![]() , то может существовать
, то может существовать![]() . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа![]() . Также может существовать
. Также может существовать 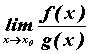 , в этом случае имеем неопределенность типа
, в этом случае имеем неопределенность типа ![]() . Если
. Если ![]() и
и ![]() , то может существовать
, то может существовать 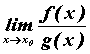 . В этом случае говорят, что имеем неопределенность типа
. В этом случае говорят, что имеем неопределенность типа![]() . Если
. Если ![]() и
и ![]() , то может существовать
, то может существовать ![]() - неопределенность типа
- неопределенность типа ![]() . Рассматривают также неопределенности типа
. Рассматривают также неопределенности типа ![]() ,
, ![]() и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой
и т. д. Основным признаком неопределенности является невозможность корректного вычисления функции простой подстановкой ![]() в выражение для функции. Полезно запомнить замечательные пределы:
в выражение для функции. Полезно запомнить замечательные пределы:
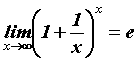 (е = 2.71828… - основание натуральных логарифмов) - неопределенность типа
(е = 2.71828… - основание натуральных логарифмов) - неопределенность типа ![]() .
.
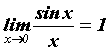 - неопределенность типа
- неопределенность типа ![]() .
.
Использование эквивалентных бесконечно малых.
Если мы имеем неопределенность типа ![]() , то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке
, то это означает, что мы вычисляем предел отношения двух бесконечно малых функций. Напомним, что функция называется бесконечно малой, если ее предел в точке ![]() равен нулю. Пусть
равен нулю. Пусть![]() ,
, ![]() ,
, ![]() ,
, ![]() - бесконечно малые функции при
- бесконечно малые функции при ![]() , причем
, причем ![]() эквивалентна
эквивалентна ![]() , т.е.
, т.е.![]() ~
~ ![]() ,
, ![]() ~
~ ![]() (напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда
(напомним, что две бесконечно малых называются эквивалентными, если предел их отношения равен 1). Тогда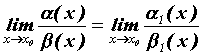 , т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную.
, т.е. при вычислении пределов отношений бесконечно малых любую из них можно заменять на эквивалентную.
Правило Лопиталя.
Неопределенности типа ![]() или
или ![]() удобно раскрывать с помощью правила Лопиталя. Пусть
удобно раскрывать с помощью правила Лопиталя. Пусть ![]() и
и ![]() две бесконечно малые или бесконечно большие функции при
две бесконечно малые или бесконечно большие функции при ![]() и существует предел отношения их производных при
и существует предел отношения их производных при ![]() . Тогда
. Тогда 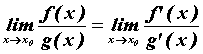 . Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.
. Если в результате применения правила Лопиталя снова получится неопределенность, то его можно применить еще раз.
Формула Тейлора.
Пусть функция ![]() имеет в точке
имеет в точке ![]() производные всех порядков до
производные всех порядков до ![]() -го включительно. Тогда для
-го включительно. Тогда для ![]() справедлива формула Тейлора:
справедлива формула Тейлора:
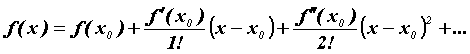
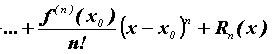
где ![]() называется остаточным членом формулы Тейлора.
называется остаточным членом формулы Тейлора.
6. Непрерывность функции в точке, на отрезке.
Рассмотрим функцию ![]() , определенную на некотором промежутке
, определенную на некотором промежутке ![]() . Функция
. Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если предел функции в точке
, если предел функции в точке ![]() равен значению функции в этой точке,
равен значению функции в этой точке,![]() .
.
Свойства функций, непрерывных на отрезке.
Функция, непрерывная в каждой точке промежутка ![]() , называется непрерывной на промежутке. Для функции, непрерывной на отрезке
, называется непрерывной на промежутке. Для функции, непрерывной на отрезке ![]() , справедливы следующие утверждения.
, справедливы следующие утверждения.
Функция, непрерывная на отрезке ![]() , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке
, достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке ![]() существуют точки
существуют точки ![]() такие, что
такие, что
![]()
![]() .
.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и принимает на концах значения разных знаков, то на интервале
и принимает на концах значения разных знаков, то на интервале ![]() существует точка
существует точка ![]() , в которой функция обращается в нуль, т.е.
, в которой функция обращается в нуль, т.е. ![]() . Это утверждение применяют для отделения корней уравнений
. Это утверждение применяют для отделения корней уравнений ![]() с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.
с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , дифференцируема хотя бы на интервале
, дифференцируема хотя бы на интервале ![]() , то на интервале
, то на интервале ![]() существует точка
существует точка ![]() , такая, что
, такая, что ![]() . Это свойство называют формулой Лагранжа или формулой конечных приращений.
. Это свойство называют формулой Лагранжа или формулой конечных приращений.
7. Классификация точек разрыва
Рассмотрим функцию ![]() , определенную на некотором промежутке
, определенную на некотором промежутке ![]() . Функция
. Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если предел функции в точке
, если предел функции в точке ![]() равен значению функции в этой точке,
равен значению функции в этой точке, ![]() .
.
Односторонние пределы функции в точке.
Функция, непрерывная в каждой точке промежутка ![]() , называется непрерывной на промежутке. Если функция
, называется непрерывной на промежутке. Если функция![]() определена на промежутке
определена на промежутке![]() ,
, ![]() , то при исследовании поведения функции
, то при исследовании поведения функции![]() в окрестности точки
в окрестности точки ![]() имеет смысл говорить о пределе функции в точке
имеет смысл говорить о пределе функции в точке ![]() справа, а при исследовании в окрестности точки
справа, а при исследовании в окрестности точки ![]() - о пределе функции в точке
- о пределе функции в точке ![]() слева. Число
слева. Число ![]() называется пределом справа функции
называется пределом справа функции ![]() при
при ![]() , стремящемся к
, стремящемся к![]() , если для любого положительного числа
, если для любого положительного числа ![]() , как бы мало оно ни было, существует такое положительное число
, как бы мало оно ни было, существует такое положительное число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , справедливо неравенство
, справедливо неравенство ![]() . Говорят “предел справа функции в точке
. Говорят “предел справа функции в точке ![]() ” и обозначают
” и обозначают ![]() . Аналогично говорят “предел слева функции
. Аналогично говорят “предел слева функции![]() в точке
в точке![]() ” и обозначают
” и обозначают ![]() , если для любого положительного числа
, если для любого положительного числа ![]() , как бы мало оно ни было, существует такое положительное число
, как бы мало оно ни было, существует такое положительное число ![]() , что для всех
, что для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству![]() , справедливо неравенство
, справедливо неравенство ![]() . Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция
. Для существования предела функции в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы функции в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Функция![]() , определенная на отрезке
, определенная на отрезке ![]() ,
, ![]() , непрерывна справа в точке
, непрерывна справа в точке ![]() , если
, если![]() и непрерывна слева в точке
и непрерывна слева в точке ![]() , если
, если![]() . Для того чтобы функция была непрерывна в точке
. Для того чтобы функция была непрерывна в точке ![]() необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:
необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:![]() . Если хотя бы одно из равенств нарушается, говорят о разрыве в точке
. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке ![]() .
.
Классификация разрывов.
Если хотя бы одно из равенств ![]() нарушается, говорят о разрыве в точке
нарушается, говорят о разрыве в точке ![]() . Если
. Если ![]() и односторонние пределы конечны, то разрыв в точке
и односторонние пределы конечны, то разрыв в точке ![]() называется устранимым. Если
называется устранимым. Если ![]() и оба односторонние пределы конечны, то говорят о скачке функции в точке
и оба односторонние пределы конечны, то говорят о скачке функции в точке ![]() . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.
. Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.
8. Производная, ее вычисление, геометрический смысл.
Производная функции в точке - Пусть функция ![]() определена на промежутке
определена на промежутке ![]() . Точка
. Точка ![]() — произвольная точка из области определения функции,
— произвольная точка из области определения функции, ![]() — приращение функции в точке
— приращение функции в точке ![]() , вызванное приращением
, вызванное приращением ![]() независимой переменной
независимой переменной ![]() . Производной функции
. Производной функции ![]() по независимой переменной
по независимой переменной ![]() в точке
в точке ![]() ,
, ![]() называется предел отношения приращения функции
называется предел отношения приращения функции ![]() к приращению
к приращению ![]() при стремлении
при стремлении ![]() к нулю, т.е.
к нулю, т.е.
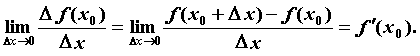
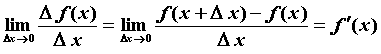 ,
,
![]() — производная функции в точке
— производная функции в точке ![]() .
.
Односторонние производные - Если ![]() определена при
определена при ![]() , то можно определить правую производную функции
, то можно определить правую производную функции ![]() в точке
в точке ![]() :
:![]()
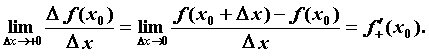
Аналогично, если ![]() определена при
определена при ![]() , определяется левая производная функции в точке
, определяется левая производная функции в точке ![]() :
:
![]()
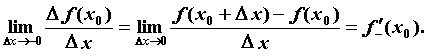
Функция ![]() имеет в точке
имеет в точке ![]() производную
производную ![]() тогда и только тогда, когда в точке
тогда и только тогда, когда в точке![]() совпадают ее левая и правая производные:
совпадают ее левая и правая производные: ![]() .
.
Секущая графика функции - Пусть ![]() — функция, определенная на промежутке
— функция, определенная на промежутке ![]() . Прямая, проходящая через точки
. Прямая, проходящая через точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() называется секущей графика функции
называется секущей графика функции ![]() . Угловой коэффициент
. Угловой коэффициент ![]() секущей равен
секущей равен 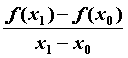 и ее уравнение имеет вид
и ее уравнение имеет вид 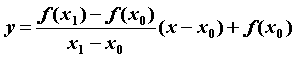 .
.
Касательная и нормаль к графику функции - Касательной к графику функции ![]() в точке
в точке ![]() называется предельное положение секущей, проходящей через точки
называется предельное положение секущей, проходящей через точки ![]() ,
, ![]() , когда
, когда ![]() . Угловой коэффициент касательной равен значению производной в точке
. Угловой коэффициент касательной равен значению производной в точке ![]() и ее уравнение имеет вид
и ее уравнение имеет вид![]() . Нормалью к графику функции
. Нормалью к графику функции ![]() в точке
в точке ![]() называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен
называется прямая , проходящая через эту точку перпендикулярно касательной. Угловой коэффициент нормали равен 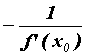 и ее уравнение имеет вид
и ее уравнение имеет вид 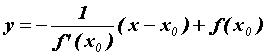 .
.
9. Производные сложных, обратных функций.
Пусть ![]() - функция, дифференцируемая в точке
- функция, дифференцируемая в точке ![]() ,
, ![]() - функция, дифференцируемая в точке
- функция, дифференцируемая в точке ![]() , причем
, причем ![]() . Тогда
. Тогда ![]() - сложная функция независимого переменного
- сложная функция независимого переменного ![]() , дифференцируема в точке
, дифференцируема в точке ![]() и ее производная в этой точке вычисляется по формуле
и ее производная в этой точке вычисляется по формуле ![]() .
.
Обычно ![]() называют внешней функцией, а
называют внешней функцией, а ![]() - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.
- внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.
Производная обратной функции.
Пусть функция ![]() дифференцируема и строго монотонна на
дифференцируема и строго монотонна на ![]() . Пусть также в точке
. Пусть также в точке ![]() производная
производная ![]() . Тогда в точке
. Тогда в точке ![]() определена дифференцируемая функция
определена дифференцируемая функция ![]() , которую называют обратной к
, которую называют обратной к ![]() , а ее производная вычисляется по формуле
, а ее производная вычисляется по формуле 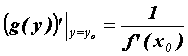 .
.
10. Дифференцируемость, дифференциал.
Дифференцируемость функции в точке.
Пусть функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() . Рассмотрим приращение функции в этой точке:
. Рассмотрим приращение функции в этой точке: ![]() . Функция
. Функция ![]() называется дифференцируемой в точке , если ее приращение можно записать в виде
называется дифференцируемой в точке , если ее приращение можно записать в виде ![]() , где
, где ![]() - приращение независимой переменной, А – постоянная, не зависящая от
- приращение независимой переменной, А – постоянная, не зависящая от ![]() ,
, ![]() - бесконечно малая функция при
- бесконечно малая функция при ![]() .
.
Дифференциал функции.
Дифференциалом функции ![]() в точке
в точке ![]() называется линейная по
называется линейная по ![]() часть
часть ![]() приращения
приращения ![]() . Дифференциал обозначается
. Дифференциал обозначается ![]() , то есть
, то есть ![]() . Рассматривая функцию
. Рассматривая функцию ![]() , нетрудно убедиться, что
, нетрудно убедиться, что ![]() , если
, если ![]() - независимая переменная.
- независимая переменная.
Связь дифференциала и производной.
Воспользуемся определением производной для дифференцируемой функции ![]() в точке
в точке ![]() :
: 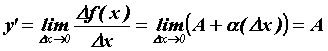 . Таким образом, дифференциал функции выражается формулой
. Таким образом, дифференциал функции выражается формулой ![]() , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на
, то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на ![]() . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.
. Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.
11. Производные и дифференциалы высших порядков.
Производные высших порядков.
Рассмотрим функцию ![]() , определенную на некотором промежутке
, определенную на некотором промежутке ![]() . Вычислим производную
. Вычислим производную ![]() , которая также является функцией на
, которая также является функцией на ![]() . Производной второго порядка от функции
. Производной второго порядка от функции ![]() называется производная от ее производной:
называется производная от ее производной: ![]() . Аналогично определяют производную любого порядка:
. Аналогично определяют производную любого порядка: ![]() .
.
Дифференциалы высших порядков.
Рассмотрим дифференциал функции ![]() в произвольной точке промежутка
в произвольной точке промежутка ![]() :
: ![]() . Здесь
. Здесь ![]() - приращение независимой переменной, которое является числом и не зависит от
- приращение независимой переменной, которое является числом и не зависит от ![]() . Сам же дифференциал есть функция от
. Сам же дифференциал есть функция от ![]() , и можно вычислить дифференциал от этой функции:
, и можно вычислить дифференциал от этой функции: ![]() При
При ![]() этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле
этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле ![]() Аналогично вычисляется дифференциал любого порядка
Аналогично вычисляется дифференциал любого порядка ![]() .
.
Понятие инвариантности формы дифференциала.
Рассмотрим дифференциал функции ![]() в произвольной точке промежутка
в произвольной точке промежутка ![]() :
: ![]() . Здесь
. Здесь ![]() - приращение независимой переменной, которое является числом и не зависит от
- приращение независимой переменной, которое является числом и не зависит от ![]() . Пусть теперь
. Пусть теперь ![]() - функция независимого переменного
- функция независимого переменного ![]() , определенная на промежутке
, определенная на промежутке ![]() . Тогда
. Тогда ![]() - сложная функция переменного
- сложная функция переменного ![]() . Вычислим ее дифференциал, используя формулу для производной сложной функции:
. Вычислим ее дифференциал, используя формулу для производной сложной функции: ![]() . Заметим, что
. Заметим, что ![]() и выражение для дифференциала принимает ту же форму
и выражение для дифференциала принимает ту же форму ![]() , хотя здесь
, хотя здесь ![]() уже функция переменного
уже функция переменного ![]() . Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что
. Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что ![]() - функция переменного
- функция переменного ![]() . Поэтому
. Поэтому ![]() и форма второго (а также и всех следующих) дифференциала неинвариантна.
и форма второго (а также и всех следующих) дифференциала неинвариантна.
12. Исследование функций и построение графиков.
Рассмотрим функцию ![]() , определенную на промежутке
, определенную на промежутке ![]() (возможно,
(возможно, ![]() ) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения.
) . Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения.
Если ![]() , то график функции пересекает ось абсцисс в точке
, то график функции пересекает ось абсцисс в точке ![]() .
.
Если ![]() , то график функции пересекает ось ординат в точке
, то график функции пересекает ось ординат в точке ![]() .
.
Если в точке ![]() функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту
функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту ![]() (Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты
(Если расстояние от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой. В случае бесконечного разрыва расстояние от кривой до вертикальной асимптоты ![]() стремится к нулю при
стремится к нулю при ![]() справа, слева или с обеих сторон).
справа, слева или с обеих сторон).
Если![]() ,
, ![]() или
или ![]() , существуют и конечны пределы
, существуют и конечны пределы 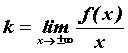 и
и ![]() , то прямая
, то прямая ![]() — асимптота графика функции.
— асимптота графика функции.
Если ![]() , то график функции имеет на левой границе области сходимости вертикальную асимптоту
, то график функции имеет на левой границе области сходимости вертикальную асимптоту ![]() ; аналогично, если
; аналогично, если ![]() , то график функции имеет на правой границе области сходимости вертикальную асимптоту
, то график функции имеет на правой границе области сходимости вертикальную асимптоту ![]() .
.
Если ![]() и существует такое число
и существует такое число ![]() , что
, что ![]() для любого
для любого ![]() , то исследуемая функция периодична с периодом
, то исследуемая функция периодична с периодом ![]() ; в этом случае достаточно построить график функции на промежутке
; в этом случае достаточно построить график функции на промежутке ![]() и доопределить его по периодичности на всю числовую ось.
и доопределить его по периодичности на всю числовую ось.
Если ![]() , то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке
, то исследуемая функция четная; этом случае график симметричен относительно оси ординат; достаточно построить график функции на промежутке ![]() и отобразить его симметрично относительно оси ординат на
и отобразить его симметрично относительно оси ординат на ![]() .
.
Если ![]() , то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке
, то исследуемая функция нечетная; этом случае график симметричен относительно начала координат; достаточно построить график функции на промежутке ![]() и отобразить его симметрично относительно начала координат на
и отобразить его симметрично относительно начала координат на ![]() .
.
Исследование функций с помощью производной.
Если функция дифференцируема на промежутке ![]() , за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения.
, за исключением, быть может, конечного числа точек этого промежутка, то можно дополнить изучение поведения функции исследованием на экстремум (точки максимума и точки минимума функции имеют общее название — точки экстремума), используя следующие утверждения.
Для того, чтобы дифференцируемая на ![]() функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы
функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы ![]() (
(![]() ) на
) на ![]() .
.
Пусть в точке ![]() производная
производная ![]() или не существует. Если существует окрестность точки
или не существует. Если существует окрестность точки ![]() , такая, что для
, такая, что для ![]() из этой окрестности
из этой окрестности ![]() при
при ![]() и
и ![]() при
при![]() , то функция имеет в точке
, то функция имеет в точке![]() максимум. Если же
максимум. Если же ![]() при
при ![]() и
и ![]() при
при ![]() , то функция имеет в точке
, то функция имеет в точке ![]() минимум (в этом случае говорят, что “производная меняет знак при переходе через точку
минимум (в этом случае говорят, что “производная меняет знак при переходе через точку ![]() ”).
”).
Если непрерывная в точке![]() функция
функция ![]() дифференцируема на
дифференцируема на ![]() , при этом
, при этом![]() на
на ![]() и
и ![]() на
на ![]() , то функция имеет в точке
, то функция имеет в точке ![]() максимум; если же
максимум; если же ![]() при
при ![]() и
и ![]() при
при ![]() , то функция имеет в точке
, то функция имеет в точке ![]() минимум.
минимум.
Исследование функций с помощью второй производной.
Если функция дважды дифференцируема на промежутке ![]() , за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.
, за исключением, быть может, конечного числа точек этого промежутка, то исследование поведения функции можно дополнить исследованием выпуклости и вогнутости.
График функции ![]() называется выпуклым (выпуклым вниз) на промежутке
называется выпуклым (выпуклым вниз) на промежутке ![]() , если он расположен выше касательной, проведенной в любой точке
, если он расположен выше касательной, проведенной в любой точке ![]() ,
, ![]() . Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх).
. Если же график функции лежит ниже касательной, — то он называется вогнутым (выпуклым вверх).
Если дважды дифференцируемая на промежутке ![]() функция
функция ![]() имеет на нем положительную вторую производную, то функция выпуклая на
имеет на нем положительную вторую производную, то функция выпуклая на ![]() . Если же вторая производная отрицательна на промежутке
. Если же вторая производная отрицательна на промежутке ![]() , то функция на нем вогнута.
, то функция на нем вогнута.
Если вторая производная равна нулю в точке ![]() , а слева и справа от нее имеет значения разных знаков, точка
, а слева и справа от нее имеет значения разных знаков, точка ![]() — точка перегиба.
— точка перегиба.
13. Кривые на плоскости.
Кривые на плоскости в декартовых координатах.
Кривая на плоскости в прямоугольных (декартовых) координатах — это множество точек, координаты которых ![]() связаны соотношениями
связаны соотношениями ![]() ,
, ![]() ,
, ![]() ,
, ![]() или
или ![]() ; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением
; первые два соотношения задают кривую явно, последнее — неявно. Кривая, заданная уравнением ![]() ,
, ![]() , называется гладкой, если функция
, называется гладкой, если функция ![]() дифференцируема на промежутке
дифференцируема на промежутке ![]() . В каждой точке
. В каждой точке![]() гладкой кривой можно провести касательную , уравнение которой
гладкой кривой можно провести касательную , уравнение которой ![]() . Уравнение нормали в той же точке имеет вид
. Уравнение нормали в той же точке имеет вид 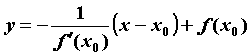 или
или ![]() . Кривая, заданная неявно уравнением
. Кривая, заданная неявно уравнением ![]() , называется гладкой, если на ней нет особых точек (точка
, называется гладкой, если на ней нет особых точек (точка ![]() линии
линии ![]() называется особой, если в ней одновременно обращаются в нуль обе частные производные функции
называется особой, если в ней одновременно обращаются в нуль обе частные производные функции ![]() :
: ![]() ). Уравнения касательной и нормали к такой кривой, проходящих через точку
). Уравнения касательной и нормали к такой кривой, проходящих через точку ![]() ,
, ![]() , имеют соответственно вид
, имеют соответственно вид ![]() и
и ![]()
Кривые, заданные параметрически.
Уравнения ![]() ,
, ![]() , устанавливающие зависимость декартовых координат
, устанавливающие зависимость декартовых координат ![]() точки плоскости от значения параметра
точки плоскости от значения параметра ![]() , определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции
, определяют на плоскости кривую, заданную в параметрической форме (говорят еще — заданную параметрически). Поскольку производная функции ![]() , заданной параметрически уравнениями
, заданной параметрически уравнениями ![]() , в точке, которая не является особой точкой кривой, вычисляется по формуле
, в точке, которая не является особой точкой кривой, вычисляется по формуле 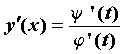 , то уравнения касательной и нормали к кривой, проходящих через точку
, то уравнения касательной и нормали к кривой, проходящих через точку ![]() , имеют соответственно вид:
, имеют соответственно вид: 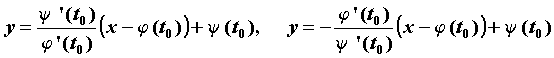 .
.
Кривые в полярных координатах.
Декартовы координаты точки ![]() на плоскости связаны с полярными координатами
на плоскости связаны с полярными координатами![]() соотношениями
соотношениями![]() . Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид
. Многие кривые на плоскости удобно описывать как функции радиуса-вектора и полярного угла — в полярных координатах. Так, уравнение единичной окружности в полярных координатах имеет вид ![]() . Уравнение кривой в полярных координатахобычно имеет вид
. Уравнение кривой в полярных координатахобычно имеет вид ![]() . Угловой коэффициент касательной к графику функции, заданной уравнением
. Угловой коэффициент касательной к графику функции, заданной уравнением ![]() , в точке
, в точке ![]() равен
равен ![]() , а декартовы координаты точки
, а декартовы координаты точки ![]() равны соответственно
равны соответственно ![]() и
и ![]() .
.
14. Формула Тейлора.
Остаточный член формулы Тейлора - Пусть функция ![]() имеет в точке
имеет в точке ![]() производные всех порядков до
производные всех порядков до ![]() -го включительно. Тогда для
-го включительно. Тогда для ![]() справедлива формула Тейлора:
справедлива формула Тейлора:
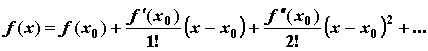
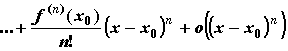 ,
,
где ![]() , называется остаточным членом формулы Тейлора в форме Пеано;
, называется остаточным членом формулы Тейлора в форме Пеано; ![]() — бесконечно малая более высокого порядка малости, чем
— бесконечно малая более высокого порядка малости, чем ![]() . Если отбросить остаточный член, то получится приближенная формула Тейлора
. Если отбросить остаточный член, то получится приближенная формула Тейлора
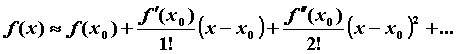
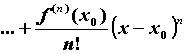 ,
,
правая часть которой называется многочленом Тейлора функции ![]() ; его обозначают
; его обозначают![]() . Приближенная формула
. Приближенная формула ![]() позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора.
позволяет заменять в различных математических расчетах (аналитических и численных) произвольную функцию ее многочленом Тейлора.
Из формулы Тейлора видно, что чем точка ![]() ближе к точке
ближе к точке ![]() , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки
, тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена. Это означает, в свою очередь, что чем больше производных имеет функция в некоторой окрестности точки ![]() , тем выше точность, с которой многочлен Тейлора
, тем выше точность, с которой многочлен Тейлора ![]() аппроксимирует функцию в этой окрестности.
аппроксимирует функцию в этой окрестности.
Разложение основных элементарных функций - Положив ![]() и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:
и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:
-
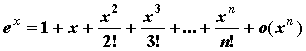 ;
; -
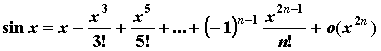 ;
; -
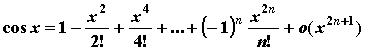 ;
; -
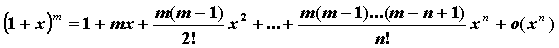 ;
; -
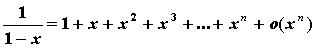 ;
; -
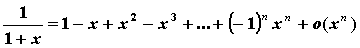 ;
; -
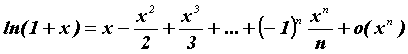 .
.
Разложение функций с использованием стандартных разложений - Для разложения по формуле Тейлора функции в окрестности произвольной точки![]() необходимо сделать замену переменной
необходимо сделать замену переменной ![]() , то есть
, то есть ![]() , и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки
, и воспользоваться одним из приведенных выше разложений основных функций в окрестности точки ![]() .
.
15. Неопределенный интеграл, простейшие методы интегрирования.
Первообразная и неопределенный интеграл - Рассмотрим функцию ![]() , определенную на промежутке
, определенную на промежутке ![]() (здесь возможно
(здесь возможно ![]() ). Дифференцируемая на промежутке
). Дифференцируемая на промежутке ![]() функция
функция ![]() , производная которой в каждой точке равна
, производная которой в каждой точке равна ![]() , называется первообразной функции
, называется первообразной функции ![]() :
: ![]() . Поскольку
. Поскольку ![]() , то можно говорить о семействе первообразных — множестве функций вида
, то можно говорить о семействе первообразных — множестве функций вида ![]() ,
, ![]() . Семейство первообразных
. Семейство первообразных ![]() функции
функции ![]() называется неопределенным интегралом функции
называется неопределенным интегралом функции ![]() и обозначается символом
и обозначается символом ![]() :
:![]() для всех
для всех ![]() . Здесь
. Здесь ![]() — знак интеграла,
— знак интеграла, ![]() — подынтегральное выражение,
— подынтегральное выражение, ![]() — подынтегральная функция,
— подынтегральная функция, ![]() — переменная интегрирования,
— переменная интегрирования, ![]() — значение неопределенного интеграла, семейство первообразных функции
— значение неопределенного интеграла, семейство первообразных функции ![]() ,
, ![]() . То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот,
. То есть производнаянеопределенного интеграла равна подынтегральной функции. Наоборот, ![]() , следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность:
, следовательно, дифференцирование и вычисление неопределенного интеграла, – взаимно обратные операции. Не представляет труда с помощью таблицы производных составить таблицу неопределенных интегралов. Важным свойством неопределенного интеграла является линейность:![]() , здесь
, здесь ![]() - постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов.
- постоянные. Вычисление неопределенного интеграла обычно сводится к преобразованию подынтегрального выражения так, чтобы можно было воспользоваться таблицей интегралов.
Интегрирование заменой переменной - Если ![]() — непрерывно дифференцируемая функция, то, полагая
— непрерывно дифференцируемая функция, то, полагая ![]() , получим формулу интегрирования заменой переменной
, получим формулу интегрирования заменой переменной ![]() . Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному.
. Если замена переменной выбрана правильно, то интеграл в правой части должен легко вычисляться. Для некоторых классов функций существуют стандартные замены, сводящие интеграл к табличному.
Интегрирование по частям - Пусть ![]() - непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям
- непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям ![]() . Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть”
. Название “по частям” связано с тем, что для записи интеграла в правой части нужно проинтегрировать “часть” ![]() подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида
подынтегрального выражения в левой части. Метод интегрирования по частям используется для интегралов вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() и некоторых других.
и некоторых других.
16. Интегрирование некоторых классов функций.
Интегрирование рациональных функций - Функция ![]() называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов:
называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: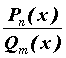 . Если
. Если ![]() , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого:
, рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого:
Если ![]() , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена
, выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена ![]() , а именно:
, а именно:
Каждому действительному корню![]() кратности 1 в разложении соответствует член
кратности 1 в разложении соответствует член 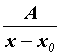 .
.
Каждому действительному корню ![]() кратности
кратности ![]() в разложении соответствует набор из
в разложении соответствует набор из ![]() членов
членов 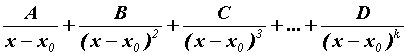 .
.
Каждой паре комплексно сопряженных корней ![]() кратности 1 в разложении соответствует член
кратности 1 в разложении соответствует член 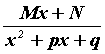 (
(![]() - корни уравнения
- корни уравнения ![]() ).
).
Каждой паре комплексно сопряженных корней кратности ![]() в разложении соответствует набор из
в разложении соответствует набор из ![]() членов
членов 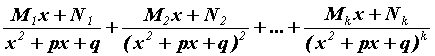 .
.
В приведенных выражениях ![]() - неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях
- неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю , приравнивая полученные коэффициенты при степенях ![]() к соответствующим коэффициентам
к соответствующим коэффициентам ![]() и решая систему относительно
и решая систему относительно ![]() .
.
Наконец, полученное разложение интегрируем почленно.
Интегрирование тригонометрических функций - Интегралы вида ![]() , где
, где ![]() - рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной
- рациональная функция своих аргументов, вычисляются с помощью универсальной замены переменной 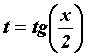 . При этом
. При этом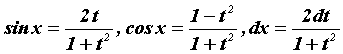 . Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать.
. Однако универсальная замена обычно связана с большими вычислениями, поэтому в некоторых случаях можно ее избежать.
Интегралы вида ![]() вычисляются с помощью замены
вычисляются с помощью замены ![]() . Интегралы вида
. Интегралы вида ![]() вычисляются с помощью замены
вычисляются с помощью замены ![]() . Интегралы вида
. Интегралы вида ![]() , если
, если ![]() , то есть четная рациональная функция своих аргументов вычисляются с помощью замены
, то есть четная рациональная функция своих аргументов вычисляются с помощью замены ![]() .
.
Интегралы вида ![]() вычисляются с помощью формул понижения степени
вычисляются с помощью формул понижения степени 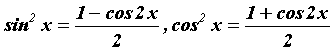 .
.
Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен.
Интегралы вида 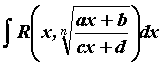 , где
, где ![]() - рациональная функция своих аргументов, вычисляются заменой
- рациональная функция своих аргументов, вычисляются заменой 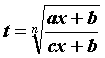 .
.
Интегралы вида ![]() вычисляются заменой
вычисляются заменой ![]() или
или![]() .
.
Интегралы вида ![]() вычисляются заменой
вычисляются заменой 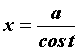 или
или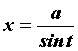 . Интегралы вида
. Интегралы вида ![]() вычисляются заменой
вычисляются заменой ![]() или
или![]() .
.
17. Определенный интеграл. Формула Ньютона-Лейбница.
Определенный интеграл, его геометрический смысл.
Рассмотрим функцию ![]() , определенную на промежутке
, определенную на промежутке ![]() . Разобьем промежуток на
. Разобьем промежуток на ![]() произвольных частей точками
произвольных частей точками ![]() и обозначим
и обозначим ![]() ,
, ![]() ,
, ![]() . На каждом промежутке
. На каждом промежутке ![]() возьмем произвольную точку
возьмем произвольную точку ![]() и вычислим в ней значение функции
и вычислим в ней значение функции![]() . Выражение
. Выражение ![]() называется интегральной суммой функции
называется интегральной суммой функции ![]() на
на ![]() .Если при
.Если при ![]() существует и конечен предел последовательности частичных сумм
существует и конечен предел последовательности частичных сумм ![]() , не зависящий ни от способа разбиения промежутка
, не зависящий ни от способа разбиения промежутка ![]() точками
точками ![]() , ни от выбора
, ни от выбора ![]() , то этот предел называют определенным интегралом от функции
, то этот предел называют определенным интегралом от функции![]() по промежутку
по промежутку ![]() , а саму функцию — интегрируемой на
, а саму функцию — интегрируемой на ![]() . Обозначают
. Обозначают 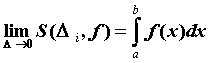 .
.
Из приведенного определения естественно следует геометрический смысл определенного интеграла: если ![]() , то
, то 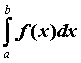 равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми
равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми ![]() .
.
Формула Ньютона-Лейбница.
Значение определенного интеграла может быть вычислено по формуле Ньютона-Лейбница 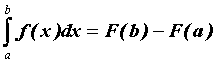 =
=![]() , здесь символ
, здесь символ ![]() означает, что из значения
означает, что из значения ![]() при верхнем пределе b нужно вычесть значение при нижнем пределе a ,
при верхнем пределе b нужно вычесть значение при нижнем пределе a , ![]() — первообразная функция для
— первообразная функция для ![]() . Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла.
. Таким образом, вычисление определенного интеграла сводится к нахождению первообразной, то есть неопределенного интеграла.
Методы вычисления определенного интеграла.
Если ![]() — непрерывно дифференцируемая на отрезке
— непрерывно дифференцируемая на отрезке ![]() функция,
функция, ![]() ,
, ![]() и
и ![]() , когда
, когда ![]() изменяется на
изменяется на ![]() , то, положив
, то, положив ![]() , получим формулу замены переменной в определенном интеграле
, получим формулу замены переменной в определенном интеграле 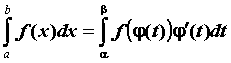 .
.
Пусть ![]() - непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям
- непрерывно дифференцируемые функции. Тогда справедлива формула интегрирования по частям 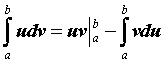 . Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.
. Эта формула применяется для тех же классов функций, что и при вычислении неопределенного интеграла.
18. Применение определенного интеграла для площадей и длин дуг.
Вычисление площадей и длин дуг кривых в декартовых координатах.
Пусть на плоскости ![]() задана область, ограниченная снизу кривой
задана область, ограниченная снизу кривой ![]() , заданной в декартовых координатах, сверху – кривой
, заданной в декартовых координатах, сверху – кривой ![]() , слева – прямой
, слева – прямой ![]() (ее может и не быть, если
(ее может и не быть, если ![]() ), справа – прямой
), справа – прямой ![]() . Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле
. Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле 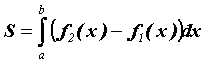 . Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например,
. Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, ![]() , то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.
, то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.
Пусть на отрезке ![]() уравнением
уравнением ![]() задана плоская кривая. Ее длина вычисляется по формуле
задана плоская кривая. Ее длина вычисляется по формуле 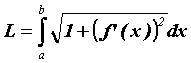
Вычисление площадей и длин дуг при параметрическом задании кривых.
Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть 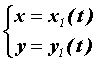 , при этом
, при этом ![]() , а сверху – кривой
, а сверху – кривой 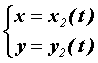 . Тогда площадь такой плоской фигуры вычисляем по формуле
. Тогда площадь такой плоской фигуры вычисляем по формуле 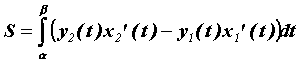 . Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что
. Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что ![]() .
.
Пусть кривая на плоскости задана параметрически 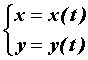
![]() . Тогда длина этой кривой вычисляется по формуле
. Тогда длина этой кривой вычисляется по формуле 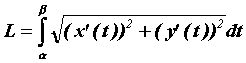 .
.
Вычисление площадей и длин дуг кривых в полярных координатах.
Когда кривая, ограничивающая область, задана в полярных координатах ![]() , то площадь этой области вычисляем по формуле
, то площадь этой области вычисляем по формуле 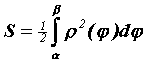 . Основная трудность в использовании этой формулы заключается в определении пределов интегрирования
. Основная трудность в использовании этой формулы заключается в определении пределов интегрирования ![]() . Здесь нужно понимать, что кривая
. Здесь нужно понимать, что кривая ![]() определена только, если
определена только, если ![]() . Поскольку в формуле присутствует
. Поскольку в формуле присутствует ![]() , то она учтет и не существующую площадь, когда
, то она учтет и не существующую площадь, когда ![]() . Решив уравнение
. Решив уравнение ![]() , найдем пределы интегрирования.
, найдем пределы интегрирования.
Если кривая, ограничивающая область, задана в полярных координатах ![]() , то ее длина вычисляется по формуле
, то ее длина вычисляется по формуле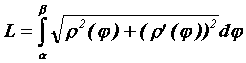 . Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.
. Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.
19. Несобственные интегралы.
Интеграл как функция верхнего предела.
Для функции ![]() , интегрируемой для всех
, интегрируемой для всех ![]() , значение интеграла
, значение интеграла 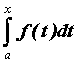 зависит от значения верхнего предела
зависит от значения верхнего предела ![]() ; можно рассмотреть функцию переменной
; можно рассмотреть функцию переменной ![]() : каждому значению
: каждому значению ![]() ставится в соответствие число, равное значению интеграла
ставится в соответствие число, равное значению интеграла .gif) . Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела:
. Таким образом, можно рассматривать определенный интеграл как функцию верхнего предела: 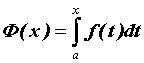 ; функция
; функция ![]() определена в области интегрируемости подынтегральной функции
определена в области интегрируемости подынтегральной функции ![]() . Если
. Если ![]() — первообразная для
— первообразная для ![]() , то значение
, то значение ![]() можно вычислить по формуле Ньютона—Лейбница:
можно вычислить по формуле Ньютона—Лейбница: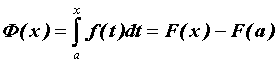 . Функцию
. Функцию 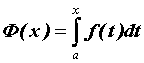 можно исследовать, не вычисляя первообразной. Для интегрируемой при
можно исследовать, не вычисляя первообразной. Для интегрируемой при![]() функции
функции ![]() справедливы следующие утверждения:
справедливы следующие утверждения: ![]() непрерывна на промежутке
непрерывна на промежутке ![]() , причем
, причем ![]() ; если
; если ![]() при
при ![]() , то
, то ![]() монотонно возрастает на промежутке
монотонно возрастает на промежутке ![]() ; если
; если ![]() непрерывна при
непрерывна при ![]() , то
, то ![]() дифференцируема на промежутке
дифференцируема на промежутке ![]() , причем
, причем 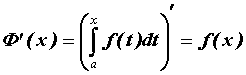 .
.
Несобственные интегралы по неограниченному промежутку.
Пусть функция ![]() интегрируема для всех
интегрируема для всех ![]() и
и 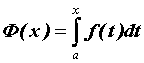 . Если существует предел
. Если существует предел 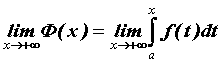 , то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его
, то этот предел называют несобственным интегралом по неограниченному промежутку и обозначают его 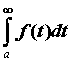 . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле
. Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле 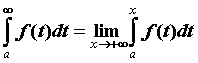 . Аналогично определен интеграл
. Аналогично определен интеграл 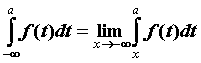 для интегрируемой при
для интегрируемой при ![]() функции
функции ![]() и интеграл
и интеграл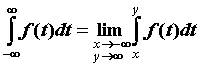 для функции , интегрируемой на
для функции , интегрируемой на ![]() . Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
. Если рассмотренные пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
Несобственные интегралы от неограниченных функций.
Пусть функция ![]() интегрируема на любом отрезке, целиком содержащемся в промежутке
интегрируема на любом отрезке, целиком содержащемся в промежутке![]() , и бесконечно большая в точке
, и бесконечно большая в точке ![]() . Если существует предел
. Если существует предел 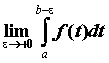 , то этот предел называют несобственным интегралом от неограниченной функции
, то этот предел называют несобственным интегралом от неограниченной функции ![]() по
по ![]() и обозначают его
и обозначают его 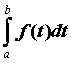 . Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле
. Если предел конечен, то говорят, что несобственный интеграл сходится и его значение вычисляют по формуле 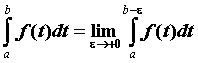 . Аналогично определен интеграл
. Аналогично определен интеграл 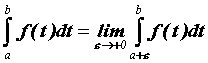 от интегрируемой на любом конечном отрезке, содержащемся в
от интегрируемой на любом конечном отрезке, содержащемся в ![]() , бесконечно большой в точке
, бесконечно большой в точке ![]() функции
функции ![]() . Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
. Если пределы бесконечны, то говорят, что соответствующий несобственный интеграл расходится.
Исследование несобственных интегралов на сходимость.
Вычисление несобственных интегралов сводится к вычислению первообразной, использованию формулы Ньютона-Лейбница и вычислению предела. Каждый из этапов сам по себе достаточно сложен, и разумно приступать к ним, если есть уверенность, что интеграл сходится, то есть предел конечен. Поэтому, в конечном счете, самым важным в теории несобственных интегралов является исследование их на сходимость: если интеграл расходится, то его и вычислять не надо. Одним из главных инструментов исследования несобственных интегралов на сходимость являются теоремы сравнения.
Рассмотрим две неотрицательные функции ![]() и
и ![]() , определенные при
, определенные при ![]() . Пусть
. Пусть ![]() для всех
для всех ![]() , начиная с некоторого числа
, начиная с некоторого числа ![]() . Тогда, если сходится интеграл от большей функции
. Тогда, если сходится интеграл от большей функции 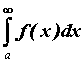 , то сходится и интеграл от меньшей, то есть
, то сходится и интеграл от меньшей, то есть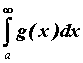 . Если расходится интеграл от меньшей функции
. Если расходится интеграл от меньшей функции .gif) ,то расходится и интеграл от большей -
,то расходится и интеграл от большей - .gif) .
.
Если 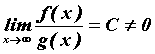 , то несобственные интегралы от этих функций или оба сходятся или оба расходятся.
, то несобственные интегралы от этих функций или оба сходятся или оба расходятся.
Аналогичные утверждения, которые называют признаками сравнения, имеют место и для интегралов по конечному промежутку от неограниченных функций.
20. Числовые ряды.
Числовой ряд. Рассмотрим произвольную числовую последовательность ![]() и формально составим сумму ее членов
и формально составим сумму ее членов 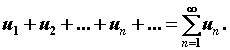 Это выражение называют числовым рядом, или просто рядом. Члены последовательности
Это выражение называют числовым рядом, или просто рядом. Члены последовательности ![]() называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда
называют членами ряда. Конечно, невозможно вычислить сумму бесконечного числа слагаемых, но легко вычислить сумму первых n членов ряда ![]() . Эта сумма называется n-ой частичной суммой.
. Эта сумма называется n-ой частичной суммой.
Сходимость числового ряда. Ряд ![]() называют сходящимся, если существует и конечен предел последовательности
называют сходящимся, если существует и конечен предел последовательности ![]() частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают
частичных сумм ряда. Сам предел при этом называют суммой ряда и обозначают ![]() ,
, 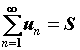 . Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность
. Если предел частичных сумм не существует или бесконечен, то ряд расходится. Разность ![]() называется остатком ряда. Очевидно, что для сходящегося ряда
называется остатком ряда. Очевидно, что для сходящегося ряда ![]() . Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то
. Это означает, что сумму сходящегося ряда можно вычислить с любой точностью, заменяя ее частичной суммой соответствующего порядка. Для расходящегося ряда это не так. Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то ![]() (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.
(необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться.
Суммирование числовых рядов. Если возможно найти общий член последовательности ![]() , то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.
, то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.
21. Сходимость знакоположительных рядов.
Теоремы сравнения.
1. Рассмотрим два числовых ряда с неотрицательными членами ![]() и
и ![]() ,
, ![]() . Если при всех n, начиная с некоторого номера,
. Если при всех n, начиная с некоторого номера, ![]() , то из сходимости ряда
, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда![]() . Наоборот, из расходимости ряда
. Наоборот, из расходимости ряда![]() следует расходимость ряда
следует расходимость ряда![]() .
.
2. Если для таких же двух рядов 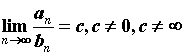 , то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд
, то оба ряда или сходятся или расходятся одновременно. При использовании теорем сравнения нужно иметь ряд-эталон, с которым сравнивать и про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд 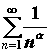 , который сходится при
, который сходится при![]() и расходится при
и расходится при ![]() , или геометрический ряд
, или геометрический ряд 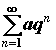 , который сходится при
, который сходится при ![]() и расходится при
и расходится при ![]() .
.
Признаки сходимости. Признаки сходимости Даламбера. Для ряда с положительными членами ![]()
![]() , вычислим
, вычислим 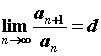 . Если
. Если ![]() , то ряд сходится,
, то ряд сходится, ![]() - расходится. При
- расходится. При ![]() признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться.
признак Даламбера ответа не дает: ряд может как сходиться, так и расходиться.
Признак сходимости Коши. Для ряда с неотрицательными членами ![]() ,
,![]() вычислим
вычислим ![]() . Если
. Если ![]() , то ряд сходится,
, то ряд сходится, ![]() - расходится. При
- расходится. При ![]() признак Коши ответа не дает: ряд может как сходиться, так и расходиться.
признак Коши ответа не дает: ряд может как сходиться, так и расходиться.
22. Сходимость знакопеременных рядов.
Абсолютная и условная сходимость. Если в последовательности ![]() бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд
бесконечно много положительных и отрицательных членов, то ряд называется знакопеременным. Ряд 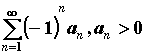 называется знакочередующимся. Знакопеременный ряд
называется знакочередующимся. Знакопеременный ряд ![]() называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 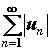 . Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда
. Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда ![]() начинают с исследования на сходимость ряда из модулей
начинают с исследования на сходимость ряда из модулей .gif) методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд
методами для рядов с неотрицательными членами. Если такой ряд сходится, то получен ответ: ряд ![]() сходится абсолютно.
сходится абсолютно.
Исследование знакочередующихся рядов. Если ряд из модулей расходится, то для знакочередующегося ряда можно применить признак Лейбница: если последовательность ![]() стремится к нулю, монотонно убывая,
стремится к нулю, монотонно убывая, ![]() , то ряд
, то ряд 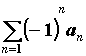 сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда:
сходится, по крайней мере, условно. Для знакочередующегося ряда очень просто оценивается остаток ряда: ![]() .
.
23. Функциональные ряды, равномерная сходимость.
Функциональный ряд, его сходимость. Рассмотрим ряд, 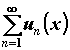 , членами которого являются функции, определенные на промежутке
, членами которого являются функции, определенные на промежутке ![]() . При каждом фиксированном
. При каждом фиксированном ![]() имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда
имеем числовой ряд, сходимость которого может быть исследована рассмотренными ранее методами. Сумма функционального ряда .gif) также является функцией от х:
также является функцией от х: ![]() . По определению предела последовательности: если для
. По определению предела последовательности: если для ![]() можно указать номер
можно указать номер ![]() ( что интересно, для каждого фиксированного
( что интересно, для каждого фиксированного ![]() - свой номер, т.е.
- свой номер, т.е. ![]() ), такой, что для
), такой, что для ![]() выполняется неравенство
выполняется неравенство ![]() , то это и означает, что функциональный ряд сходится к функции
, то это и означает, что функциональный ряд сходится к функции![]() . Множество
. Множество ![]() , для которого это выполняется, называется областью сходимости функционального ряда.
, для которого это выполняется, называется областью сходимости функционального ряда.
Равномерная сходимость функционального ряда. Пусть ![]() , т.е. функциональный ряд сходится. Если для
, т.е. функциональный ряд сходится. Если для ![]() можно указать номер
можно указать номер ![]() независимо от
независимо от ![]() , такой, что для
, такой, что для![]() выполняется неравенство
выполняется неравенство ![]() , то говорят, что функциональный ряд сходится равномерно на множестве .
, то говорят, что функциональный ряд сходится равномерно на множестве .
Исследование на равномерную сходимость. Признак Вейерштрасса равномерной сходимости функционального ряда: если существует сходящийся числовой ряд ![]() с положительными членами, такой, что для всех
с положительными членами, такой, что для всех ![]() , начиная с некоторого номера и всех
, начиная с некоторого номера и всех ![]() выполняется неравенство
выполняется неравенство![]() , то функциональный ряд
, то функциональный ряд .gif) сходится на
сходится на ![]() равномерно. Числовой ряд
равномерно. Числовой ряд ![]() в этом случае называют мажорантой для функционального ряда.
в этом случае называют мажорантой для функционального ряда.
24. Ряд Тейлора.
Степенные ряды. Функциональный ряд ![]() , где
, где ![]() - числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале
- числовая последовательность, называется степенным рядом. Степенной ряд сходится на интервале ![]() с центром в точке
с центром в точке ![]() . Число
. Число ![]() - радиус сходимости степенного ряда может быть вычислено по формулам
- радиус сходимости степенного ряда может быть вычислено по формулам 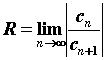 , или
, или .gif) . Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда.
. Степенной ряд сходится равномерно на любом отрезке, целиком лежащем внутри интервала сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда.
Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() и имеет в этой точке производные всех порядков. Ряд
и имеет в этой точке производные всех порядков. Ряд
![]() называется рядом Тейлора для функции
называется рядом Тейлора для функции ![]() в точке
в точке ![]() . При
. При![]() такой ряд называют также рядом Маклорена:
такой ряд называют также рядом Маклорена: ![]() . Функция
. Функция ![]() может быть разложена в степенной ряд на интервале
может быть разложена в степенной ряд на интервале ![]() , если существует степенной ряд, сходящийся к
, если существует степенной ряд, сходящийся к ![]() на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки
на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки ![]() , то это ряд Тейлора. Пусть функция
, то это ряд Тейлора. Пусть функция ![]() бесконечно дифференцируема на интервале
бесконечно дифференцируема на интервале ![]() и все ее производные ограничены в совокупности на этом интервале, то есть существует число
и все ее производные ограничены в совокупности на этом интервале, то есть существует число ![]() , такое, что для всех
, такое, что для всех ![]() и для всех
и для всех ![]() справедливо неравенство
справедливо неравенство ![]() . Тогда ряд Тейлора сходится к
. Тогда ряд Тейлора сходится к ![]() для всех
для всех ![]() . Приведем разложения в ряд Тейлора для основных элементарных функций.
. Приведем разложения в ряд Тейлора для основных элементарных функций.
.gif)
.gif)
.gif)
.gif)
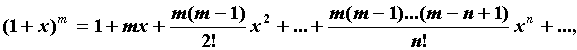
![]()
25. Ряд Фурье.
Ряд Фурье, его сходимость. Пусть функция ![]() абсолютно интегрируема на отрезке
абсолютно интегрируема на отрезке ![]() , то есть существует
, то есть существует .gif) . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье:
. Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье:.gif) . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье:
. Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: .gif)
.gif) . Если функция
. Если функция ![]() кусочно-гладкая на отрезке
кусочно-гладкая на отрезке ![]() , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если
, то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если .gif) - сумма ряда Фурье, то для любого
- сумма ряда Фурье, то для любого ![]()
.gif) . То есть, если
. То есть, если ![]() непрерывна в точке
непрерывна в точке ![]() , то
, то ![]() . Если в точке
. Если в точке ![]() у
у ![]() разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке
разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке![]() .
.
Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке ![]() функции
функции![]() задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке
задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке ![]() :
: .gif) ,
, .gif) .
.
26. Сходимость ряда Фурье.
Сходимость ряда Фурье, явление Гиббса. Если функция ![]() кусочно-гладкая на отрезке
кусочно-гладкая на отрезке ![]() , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если
, то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если .gif) - сумма ряда Фурье, то для любого
- сумма ряда Фурье, то для любого ![]()
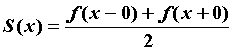 . То есть, если
. То есть, если ![]() непрерывна в точке
непрерывна в точке ![]() , то
, то ![]() . Если в точке
. Если в точке ![]() у
у ![]() разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке
разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке ![]() . В окрестности точек непрерывности функции
. В окрестности точек непрерывности функции ![]() разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при
разность между значением функции в точке и значением частичной суммы ряда в этой точке стремится к нулю при ![]() , что полностью соответствует теории, поскольку в этом случае
, что полностью соответствует теории, поскольку в этом случае ![]() . В окрестности точек разрыва
. В окрестности точек разрыва ![]() частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка
частичные суммы ряда Фурье ведут себя иначе. Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Оно состоит в том, что для некоторых функций в точке ее скачка ![]() существуют такие значения
существуют такие значения ![]() , что
, что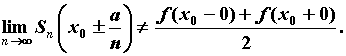
Это не противоречит теории, поскольку у Гиббса рассмотрен предел ![]() , а в теории v
, а в теории v ![]() .
.
Приближение функций, минимальное свойство коэффициентов Фурье. Функция .gif) , где
, где ![]() - произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции
- произвольные числа, называется тригонометрическим многочленом. Тригонометрическим многочленом наилучшего приближения n-ой степени для функции ![]() на отрезке
на отрезке ![]() называется такой многочлен
называется такой многочлен 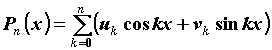 , среднеквадратичное отклонение
, среднеквадратичное отклонение ![]() которого от функции
которого от функции ![]() минимально:
минимально: 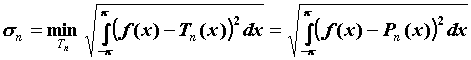 . Для любой ограниченной интегрируемой на
. Для любой ограниченной интегрируемой на ![]() функции частичная сумма
функции частичная сумма ![]() ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени.
ее ряда Фурье является тригонометрическим многочленом наилучшего приближения n-ой степени.
Зависимость скорости сходимости от гладкости функций. Скорость сходимости ряда Фурье функции![]() зависит от ее гладкости (количества непрерывных производных). Если
зависит от ее гладкости (количества непрерывных производных). Если ![]() непрерывно дифференцируема r раз на отрезке
непрерывно дифференцируема r раз на отрезке ![]() , то справедливо неравенство
, то справедливо неравенство .gif) , где
, где ![]() . Для среднеквадратичного отклонения справедлива оценка
. Для среднеквадратичного отклонения справедлива оценка 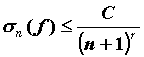 , где
, где 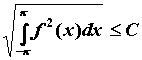 .
.
27. Функции многих переменных.
Функция двух переменных. Переменная ![]() (с областью изменения
(с областью изменения ![]() ) называется функцией независимых переменных
) называется функцией независимых переменных ![]() в множестве
в множестве ![]() , если каждой паре
, если каждой паре ![]() их значений из
их значений из ![]() по некоторому правилу или закону ставится в соответствие одно определенное значение
по некоторому правилу или закону ставится в соответствие одно определенное значение ![]() из множества
из множества ![]() . Множество
. Множество ![]() v область определения функции, множество
v область определения функции, множество ![]() v область ее значений. Функциональная зависимость
v область ее значений. Функциональная зависимость ![]() от
от ![]() обозначается так:
обозначается так: ![]() и т.п. Выберем в пространстве систему координат
и т.п. Выберем в пространстве систему координат ![]() , изобразим на плоскости
, изобразим на плоскости ![]() множество
множество ![]() ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение
; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение ![]() . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных.
. Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных.
Линии и поверхности уровня. Линией уровня функции двух переменных ![]() называется геометрическое место точек на плоскости
называется геометрическое место точек на плоскости ![]() , в которых функция
, в которых функция ![]() принимает одно и то же значение. Линии уровня функции
принимает одно и то же значение. Линии уровня функции ![]() определяются уравнением
определяются уравнением ![]() , где
, где ![]() . Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных
. Изучая линии уровня функции, можно исследовать характер ее изменения, не прибегая к пространственному графику. Поверхностью уровня функции трех переменных ![]() называется геометрическое место точек в пространстве, в которых функция
называется геометрическое место точек в пространстве, в которых функция ![]() принимает одно и то же значение. Уравнение поверхностей уровня имеет вид:
принимает одно и то же значение. Уравнение поверхностей уровня имеет вид: ![]() . Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций.
. Поскольку график функции трех переменных нам недоступен, поверхности уровня являются единственным средством изучения таких функций.
Локальные экстремумы. Точка ![]() называется точкой локального минимума (максимума) функции
называется точкой локального минимума (максимума) функции ![]() , определенной в области
, определенной в области ![]() , если существует окрестность этой точки, такая, что
, если существует окрестность этой точки, такая, что![]()
![]() для всех точек этой окрестности, отличных от
для всех точек этой окрестности, отличных от![]() . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.
. Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.
28. Частные производные, градиент.
Частные производные. Пусть ![]() - функция двух переменных, определенная в некоторой окрестности точки
- функция двух переменных, определенная в некоторой окрестности точки ![]() . Если существует конечный предел
. Если существует конечный предел 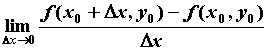 , то говорят, что функция
, то говорят, что функция ![]() имеет в точке
имеет в точке ![]() частную производную по переменной
частную производную по переменной ![]() . Аналогично определяется частная производная по
. Аналогично определяется частная производная по ![]() . Обозначают:
. Обозначают:
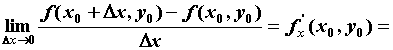
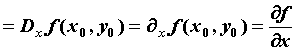 .
.
Пусть ![]() - функция n переменных, определенная в области
- функция n переменных, определенная в области ![]() n-мерного пространства. Частной производной функции
n-мерного пространства. Частной производной функции ![]() по переменной
по переменной ![]() называется предел
называется предел
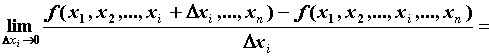
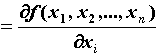 .
.
Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.
Производная по направлению. Если в n-мерном пространстве задан единичный вектор![]() , то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению:
, то изменение дифференцируемой функции в направлении этого вектора характеризуется производной по направлению: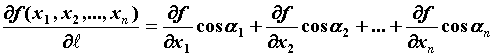 . В частности, для функции трех переменных
. В частности, для функции трех переменных 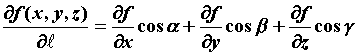 ,
, ![]() - направляющие косинусы вектора
- направляющие косинусы вектора ![]() .
.
Градиент. Производная по направлению представляет собой скалярное произведение вектора ![]() и вектора с координатами
и вектора с координатами 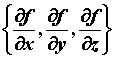 , который называется градиентом функции
, который называется градиентом функции ![]() и обозначается
и обозначается ![]() . Поскольку
. Поскольку 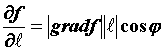 , где
, где ![]() - угол между
- угол между ![]() и
и ![]() , то вектор
, то вектор![]() указывает направление скорейшего возрастания функции
указывает направление скорейшего возрастания функции ![]() , а его модуль равен производной по этому направлению.
, а его модуль равен производной по этому направлению.
Полный дифференцал. Для приращения дифференцируемой функции ![]() справедливо равенство
справедливо равенство 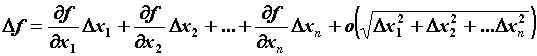 . Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции
. Линейная по приращениям аргументов часть приращения функции называется полным дифференциалом функции ![]() и обозначается
и обозначается 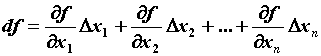 .
.
Производные и дифференциалы высших порядков. Дифференцируя частную производную как функцию нескольких переменных по одной из переменных, получим производные второго порядка. Например, для функции двух переменных: 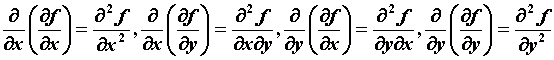 . Если смешанные производные
. Если смешанные производные ![]() и
и ![]() непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например,
непрерывны, то они равны, то есть не зависят от порядка дифференцирования. Аналогично определяются, например, 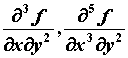 . Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов
. Если при вычислении полного дифференциала от дифференциала первого порядка учесть, что приращения аргументов ![]() есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных:
есть числа и оставить их неизменными, то получим дифференциал второго порядка. Например, для функции двух переменных: 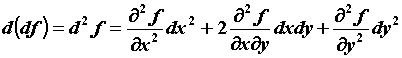 . Здесь учтено равенство смешанных производных второго порядка и принято
. Здесь учтено равенство смешанных производных второго порядка и принято ![]() . При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения:
. При этих допущениях формулу дифференциала любого порядка можно получить из символического выражения: 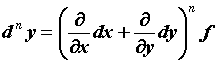 .
.
29. Неявные функции.
Неявная функция одной переменной. Пусть в некоторой области ![]() плоскости
плоскости ![]() задана функция
задана функция ![]() , и пусть линия уровня этой функции , определяемая уравнением
, и пусть линия уровня этой функции , определяемая уравнением ![]() , является графиком некоторой функции
, является графиком некоторой функции ![]() , определяемой уравнением
, определяемой уравнением ![]() . В этом случае говорят, что функция
. В этом случае говорят, что функция ![]() задана неявно уравнением
задана неявно уравнением ![]() . Для существования неявной функции требуется выполнение следующих условий: функция
. Для существования неявной функции требуется выполнение следующих условий: функция ![]() и ее частная производная по
и ее частная производная по ![]() непрерывны в
непрерывны в ![]() ,
,![]() . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки ![]() существует единственная непрерывная функция
существует единственная непрерывная функция ![]() , задаваемая уравнением
, задаваемая уравнением ![]() , так, что в этой окрестности
, так, что в этой окрестности ![]() .
.
Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение ![]() задает неявно функцию
задает неявно функцию ![]() . Это же уравнение может задавать неявно функцию
. Это же уравнение может задавать неявно функцию ![]() или
или ![]() .
.
Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение ![]() :
:.gif) . Отсюда получим формулу для производной функции
. Отсюда получим формулу для производной функции ![]() , заданной неявно:
, заданной неявно: .gif) . Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением
. Таким же способом нетрудно получить формулы для частных производных функции нескольких переменных, заданной неявно, например, уравнением ![]() :
: .gif) ,
, .gif) .
.
30. Формула Тейлора для многих переменных.
Формулы Тейлора и Маклорена. Если функция ![]() имеет в некоторой окрестности точки
имеет в некоторой окрестности точки![]() непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки
непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки ![]() из этой окрестности справедлива формула Тейлора n-го порядка:
из этой окрестности справедлива формула Тейлора n-го порядка: 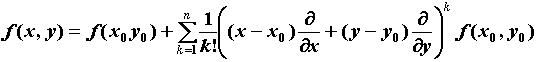
![]() , где
, где![]() ,
,
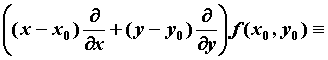
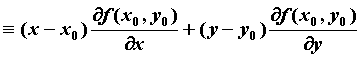 ,
,
.gif)
и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2: .gif) .
.
Аппроксимация функции многочленом. Выражение
.gif) называется многочленом Тейлора n-го порядка. Поскольку
называется многочленом Тейлора n-го порядка. Поскольку ![]() , то в окрестности точки функцию
, то в окрестности точки функцию ![]() можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т.е.
можно приближенно заменить, или, как говорят, аппроксимировать, ее многочленом Тейлора, т.е. ![]() . Чем ближе точка
. Чем ближе точка ![]() к точке
к точке ![]() , тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция
, тем выше точность такой аппроксимации; кроме того, точность возрастает с ростом n. Это означает, что, чем больше непрерывных производных имеет функция ![]() , тем точнее представляет ее многочлен Тейлора.
, тем точнее представляет ее многочлен Тейлора.
31. Исследование на экстремум.
Локальные экстремумы. Точка ![]() называется точкой локального минимума (максимума) функции
называется точкой локального минимума (максимума) функции ![]() , определенной в области
, определенной в области ![]() , если существует окрестность этой точки, такая, что
, если существует окрестность этой точки, такая, что ![]()
![]() для всех точек этой окрестности, отличных от
для всех точек этой окрестности, отличных от ![]() . Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.
. Такие экстремумы (максимумы и минимумы) называются нестрогими. Строгие экстремумы имеют место в случае, когда выполнены строгие неравенства.
Исследование на экстремум функции двух переменных. Обозначим через![]() приращение функции
приращение функции ![]() в точке
в точке ![]() . Если
. Если ![]() - точка локального минимума функции
- точка локального минимума функции ![]() , то существует окрестность
, то существует окрестность ![]() , в которой
, в которой ![]() (обратное неравенство в случае максимума). Из формулы Тейлора первого порядка
(обратное неравенство в случае максимума). Из формулы Тейлора первого порядка 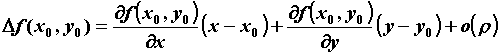 следует, что приращение
следует, что приращение ![]() дважды непрерывно дифференцируемой функции
дважды непрерывно дифференцируемой функции ![]() может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т.е. выполнено необходимое условие экстремума: если точка
может сохранять знак, если главная линейная часть приращения функции в точке экстремума (максимума или минимума) равна нулю, т.е. выполнено необходимое условие экстремума: если точка ![]() - точка экстремума, то
- точка экстремума, то .gif) . Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид
. Такая точка называется стационарной точкой функции. Приращение функции в стационарной точке имеет вид .gif) . Обозначим
. Обозначим .gif) . Справедливо следующее достаточное условие экстремума. Пусть функция
. Справедливо следующее достаточное условие экстремума. Пусть функция ![]() дважды непрерывно дифференцируема в окрестности точки
дважды непрерывно дифференцируема в окрестности точки ![]() и
и 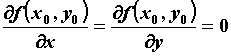 . Если
. Если ![]() , то в точке
, то в точке ![]() функция достигает экстремума. Если при этом
функция достигает экстремума. Если при этом ![]() , то этот экстремум v минимум, при
, то этот экстремум v минимум, при ![]() - максимум. Если же
- максимум. Если же ![]() , то в точке
, то в точке ![]() экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции
экстремума нет. Геометрически достаточное условие означает, что в окрестности экстремума график функции ![]() близок к поверхности
близок к поверхности![]() . Если
. Если ![]() , то для определения знака приращения
, то для определения знака приращения ![]() необходимо изучить члены формулы Тейлора более высокого порядка.
необходимо изучить члены формулы Тейлора более высокого порядка.
32. Условный экстремум.
Условные экстремумы. Пусть функция ![]() определена в некоторой области
определена в некоторой области ![]() и в этой области задана кривая уравнением
и в этой области задана кривая уравнением ![]() . Условным экстремумом функции двух переменных
. Условным экстремумом функции двух переменных ![]() называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить
называют ее экстремум при условии, что точки берутся на заданной кривой. Если из уравнения кривой можно, например, выразить ![]() , то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной
, то задача о нахождении условного экстремума сводится к исследованию на экстремум функции одной переменной ![]() .
.
Метод множителей Лагранжа. Если уравнение ![]() не разрешимо ни относительно
не разрешимо ни относительно ![]() , ни относительно
, ни относительно ![]() , то рассматривают функцию Лагранжа
, то рассматривают функцию Лагранжа![]() . Необходимым условием существования условного экстремума функции
. Необходимым условием существования условного экстремума функции ![]() при условии
при условии ![]() является равенство нулю всех частных производных функции Лагранжа:
является равенство нулю всех частных производных функции Лагранжа: 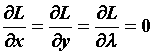 .
.
Наибольшее и наименьшее значение функции в области. Поскольку функция ![]() , непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением
, непрерывная в ограниченной замкнутой области достигает в ней своего наибольшего и наименьшего значений, задача об их нахождении разделяется на две части: найти экстремумы функции двух переменных внутри области, найти ее условные экстремумы на границе области, при условии, что граница задана уравнением ![]() .
.
33. Двойной и тройной интегралы.
Двойной интеграл в декартовых координатах. Пусть ![]() ограниченная замкнутая область плоскости
ограниченная замкнутая область плоскости ![]() с кусочно-гладкой границей и пусть функция
с кусочно-гладкой границей и пусть функция ![]() определена и ограничена на
определена и ограничена на ![]() . Посредством сетки кусочно-гладких кривых разобьем
. Посредством сетки кусочно-гладких кривых разобьем ![]() на конечное число элементарных областей
на конечное число элементарных областей ![]() с площадями
с площадями ![]() (разбиение
(разбиение ![]() ). Пусть
). Пусть ![]() - наибольший из диаметров областей
- наибольший из диаметров областей ![]() , получающийся при разбиении
, получающийся при разбиении ![]() . В каждой из элементарных областей выберем произвольную точку
. В каждой из элементарных областей выберем произвольную точку ![]() . Число
. Число 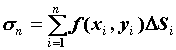 называется интегральной суммой и ставится в соответствие каждому разбиению
называется интегральной суммой и ставится в соответствие каждому разбиению ![]() и каждому выбору точек
и каждому выбору точек ![]() . Если существует
. Если существует ![]() и он не зависит от выбора разбиения
и он не зависит от выбора разбиения ![]() и точек
и точек ![]() , то функция называется интегрируемой по Риману в области
, то функция называется интегрируемой по Риману в области ![]() , а сам предел называется двойным интегралом от функции
, а сам предел называется двойным интегралом от функции ![]() по области
по области ![]() и обозначается
и обозначается ![]() или
или ![]() . Двойной интеграл существует, если
. Двойной интеграл существует, если ![]() непрерывна на
непрерывна на ![]() . Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в
. Допустимы точки разрыва первого рода, лежащие на конечном числе гладких кривых в ![]() .
.
Свойства двойного интеграла. Свойства двойного интеграла аналогичны свойствам определенного интеграла:
Линейность:
![]() . Аддитивность:
. Аддитивность:
![]() , если S1 и S2 две области без общих внутренних точек.
, если S1 и S2 две области без общих внутренних точек.
Если для каждой точки ![]() выполнено неравенство
выполнено неравенство ![]() , то
, то ![]() .
.
Если ![]() интегрируема на
интегрируема на ![]() , то функция
, то функция ![]() также интегрируема, причем
также интегрируема, причем ![]() .
.
Если ![]() и
и ![]() наименьшее и наибольшее значения функции
наименьшее и наибольшее значения функции ![]() в области, а ее
в области, а ее ![]() площадь, то
площадь, то ![]() .
.
Теорема о среднем значении: если ![]() непрерывна в связной области
непрерывна в связной области ![]() , то существует, по крайней мере, одна точка
, то существует, по крайней мере, одна точка ![]() такая, что
такая, что ![]() .
.
Вычисление двойного интеграла.
Если ![]() , где -
, где - ![]() непрерывные на
непрерывные на ![]() функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями:
функции, то двойной интеграл может быть вычислен двумя последовательными интегрированиями: .gif) . Аналогично, если
. Аналогично, если ![]() , то
, то .gif) .
.
Тройной интеграл и его свойства. Пусть ![]() - ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция
- ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция ![]() определена и ограничена в
определена и ограничена в ![]() . Посредством сетки кусочно-гладких поверхностей разобьем
. Посредством сетки кусочно-гладких поверхностей разобьем ![]() на конечное число элементарных областей
на конечное число элементарных областей ![]() с объемами
с объемами ![]() (разбиение
(разбиение![]() ). Пусть
). Пусть ![]() . наибольший из диаметров областей
. наибольший из диаметров областей ![]() , получающийся при разбиении
, получающийся при разбиении ![]() . В каждой из элементарных областей выберем произвольную точку
. В каждой из элементарных областей выберем произвольную точку ![]() . Число
. Число .gif) ставится в соответствие каждому разбиению
ставится в соответствие каждому разбиению ![]() и каждому выбору точек
и каждому выбору точек ![]() и называется интегральной суммой. Если существует
и называется интегральной суммой. Если существует ![]() и он не зависит от выбора разбиения
и он не зависит от выбора разбиения ![]() и точек,
и точек, ![]() то функция называется интегрируемой по Риману в области
то функция называется интегрируемой по Риману в области ![]() , а сам предел называется тройным интегралом от функции
, а сам предел называется тройным интегралом от функции ![]() по области
по области ![]() и обозначается
и обозначается ![]() . Свойства тройных интегралов такие же, как и у двойных интегралов.
. Свойства тройных интегралов такие же, как и у двойных интегралов.
Вычисление тройного интеграла в декартовых координатах. Пусть ![]() является цилиндрическим телом, проекция которого на плоскость
является цилиндрическим телом, проекция которого на плоскость ![]() есть область
есть область ![]() и которое ограничено снизу поверхностью
и которое ограничено снизу поверхностью ![]() , а сверху v поверхностью
, а сверху v поверхностью ![]() , где
, где ![]() - непрерывные функции в . Тогда
- непрерывные функции в . Тогда .gif) , то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области
, то есть интегрированием по z тройной интеграл сводится к двойному интегралу по области ![]() . Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.
. Для областей более сложной формы вычисление двойных и тройных интегралов производится разбиением областей на конечное число простых областей с уже рассмотренными свойствами.
34. Замена переменных в кратных интегралах.
Замена переменных в двойном интеграле. Пусть функции ![]() взаимно однозначно отображают открытое множество, содержащее область
взаимно однозначно отображают открытое множество, содержащее область ![]() плоскости
плоскости ![]() на открытое множество, содержащее область
на открытое множество, содержащее область ![]() , и пусть
, и пусть ![]() является образом
является образом ![]() . Если
. Если ![]() и их частные производные непрерывны, а определитель
и их частные производные непрерывны, а определитель .gif) , то
, то ![]() . Выражение
. Выражение ![]() называется элементом площади в криволинейных координатах, функциональный определитель
называется элементом площади в криволинейных координатах, функциональный определитель ![]() - якобианом.
- якобианом.
Вычисление площади.
Замена переменных в тройном интеграле. Пусть посредством функций ![]() производится взаимно однозначное отображение открытого множества, содержащего область
производится взаимно однозначное отображение открытого множества, содержащего область ![]() пространства
пространства ![]() на открытое множество, содержащее область
на открытое множество, содержащее область ![]() пространства
пространства ![]() и
и ![]() есть образ
есть образ ![]() . Если эти три функции непрерывны вместе со своими первыми частными производными в области
. Если эти три функции непрерывны вместе со своими первыми частными производными в области ![]() и якобиан
и якобиан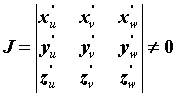 , то
, то ![]() . Выражение
. Выражение ![]() называется элементом объема в криволинейных координатах .
называется элементом объема в криволинейных координатах .
Вычисление объема.
Двойной интеграл в полярных координатах. Введем на плоскости полярные координаты. Пусть ![]() - область, полученная взаимно однозначным отображением области
- область, полученная взаимно однозначным отображением области ![]() плоскости
плоскости ![]() , определяемым функциями
, определяемым функциями ![]() . Тогда
. Тогда ![]() , а двойной интеграл в полярных координатах вычисляется по формуле:
, а двойной интеграл в полярных координатах вычисляется по формуле: ![]() .Элемент площади в полярных координатах есть
.Элемент площади в полярных координатах есть ![]() .
.
35. Сферические и цилиндрические координаты.
Тройной интеграл в цилиндрических координатах. Введем в пространстве цилиндрические координаты. Для этого на плоскости ![]() используем полярные координаты, а третья координата произвольной точки
используем полярные координаты, а третья координата произвольной точки ![]() остается
остается ![]() . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические:
. Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические: ![]() . Тогда
. Тогда ![]() и тройной интеграл в цилиндрических координатах вычисляется по формуле:
и тройной интеграл в цилиндрических координатах вычисляется по формуле: ![]() . Элемент объема в цилиндрической системе координат есть
. Элемент объема в цилиндрической системе координат есть ![]() .
.
Тройной интеграл в сферических координатах. Введем в пространстве сферическую систему координат. Для этого рассмотрим произвольную точку ![]() в декартовой системе координат. Спроектируем ее на плоскость
в декартовой системе координат. Спроектируем ее на плоскость ![]() , получив точку
, получив точку ![]() . Положение точки
. Положение точки ![]() в пространстве будем характеризовать ее расстоянием
в пространстве будем характеризовать ее расстоянием ![]() от начала координат
от начала координат ![]() , углом
, углом ![]() между отрезком
между отрезком ![]() и положительной полуосью
и положительной полуосью ![]()
![]() , углом
, углом ![]() между отрезком
между отрезком ![]() и положительной полуосью
и положительной полуосью ![]()
![]() . Декартовы координаты точки
. Декартовы координаты точки ![]() выражаются через сферические по формулам:
выражаются через сферические по формулам: ![]() . В этом случае
. В этом случае ![]() . Тогда тройной интеграл в сферических координатах вычисляется по формуле:
. Тогда тройной интеграл в сферических координатах вычисляется по формуле:
![]()
![]() .
.
Элемент объема в сферической системе координат есть ![]() .
.
36. Поверхностный интеграл по площади поверхности.
Площадь гладкой поверхности. Рассмотрим кусок поверхности ![]() , заданной уравнением
, заданной уравнением ![]() . Пусть выполняется условие
. Пусть выполняется условие ![]() , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором
, что означает, что в каждой точке поверхности существует нормаль с направляющим вектором ![]() . Разобьем поверхность
. Разобьем поверхность ![]() сеткой гладких кривых на элементарные области
сеткой гладких кривых на элементарные области ![]() ( разбиение
( разбиение ![]() ). Пусть
). Пусть ![]() - наибольший из диаметров элементарных областей. Если независимо от разбиения
- наибольший из диаметров элементарных областей. Если независимо от разбиения ![]() существует
существует .gif) , то он и называется площадью данной поверхности. Пусть
, то он и называется площадью данной поверхности. Пусть ![]() однозначно проектируется на плоскость
однозначно проектируется на плоскость ![]() и
и ![]() - эта проекция. Элементу площади
- эта проекция. Элементу площади ![]() области
области ![]() на плоскости
на плоскости ![]() соответствует элемент площади поверхности
соответствует элемент площади поверхности ![]() , равный
, равный .gif) , где
, где ![]() - угол между нормалью к поверхности
- угол между нормалью к поверхности ![]() и осью
и осью ![]() . Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла
. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла .gif) по проекции поверхности на плоскость. Если поверхность задана уравнением
по проекции поверхности на плоскость. Если поверхность задана уравнением ![]() , то
, то .gif) и площадь поверхности вычисляется по формуле
и площадь поверхности вычисляется по формуле 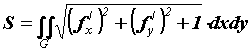 , здесь
, здесь ![]() - проекция поверхности
- проекция поверхности ![]() на плоскость
на плоскость ![]() . Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.
. Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.
Поверхностный интеграл 1-го рода. Пусть некоторая функция ![]() определена и ограничена на гладкой поверхности
определена и ограничена на гладкой поверхности ![]() . Выберем разбиение
. Выберем разбиение ![]() поверхности
поверхности ![]() и точки
и точки ![]() на каждой элементарной области
на каждой элементарной области ![]() и составим интегральную сумму
и составим интегральную сумму .gif) . Если независимо от выбора разбиения
. Если независимо от выбора разбиения ![]() и точек
и точек ![]() существует
существует ![]() , то он называется поверхностным интегралом по площади поверхности
, то он называется поверхностным интегралом по площади поверхности ![]() (1-го рода) от функции
(1-го рода) от функции ![]() и обозначается
и обозначается ![]() .
.
Свойства и вычисление поверхностного интеграла по площади поверхности. Если поверхность задана уравнением ![]() и однозначно проектируется на плоскость
и однозначно проектируется на плоскость ![]() , то поверхностный интеграл 1-го рода вычисляется по формуле
, то поверхностный интеграл 1-го рода вычисляется по формуле .gif) . Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.
. Нетрудно получить аналогичные формулы, если поверхность однозначно проектируется на другие координатные плоскости. Поскольку вычисление поверхностного интеграла сводится к двойному интегралу, то, естественно, все свойства поверхностного интеграла 1-го рода такие же, как и у двойного.
37. Криволинейный интеграл по длине дуги.
Криволинейный интеграл 1-го рода. Пусть ![]() - отрезок кусочно-гладкой кривой с началом в точке
- отрезок кусочно-гладкой кривой с началом в точке ![]() и концом в точке
и концом в точке ![]() и
и ![]() - ограниченная функция, определенная в некоторой области, содержащей кривую
- ограниченная функция, определенная в некоторой области, содержащей кривую ![]() . Выберем на кривой произвольные точки
. Выберем на кривой произвольные точки ![]() , разбивая ее на элементарные отрезки (разбиение
, разбивая ее на элементарные отрезки (разбиение ![]() ), длина каждого
), длина каждого ![]() . Обозначим
. Обозначим ![]() . Пусть
. Пусть ![]() - произвольная точка на элементарном отрезке
- произвольная точка на элементарном отрезке ![]() . Составим интегральную сумму
. Составим интегральную сумму .gif) . Если независимо от разбиения
. Если независимо от разбиения ![]() и выбора точек
и выбора точек ![]() существует
существует ![]() , то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается
, то он называется криволинейным интегралом по длине кривой (1-го рода) и обозначается ![]() . Аналогично определяется криволинейный интеграл 1-го рода
. Аналогично определяется криволинейный интеграл 1-го рода ![]() от функции трех переменных
от функции трех переменных ![]() по отрезку
по отрезку ![]() пространственной кривой.
пространственной кривой.
Свойства и вычисление криволинейного интеграла по длине дуги. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой , то есть![]() . Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если
. Это единственное свойство, которое не совпадает с обычными свойствами интегралов, определеямых через предел интегральной суммы. Если ![]() - отрезок кусочно-гладкой кривой, заданной параметрически:
- отрезок кусочно-гладкой кривой, заданной параметрически:
![]()
![]() , то криволинейный интеграл вычисляется по формуле:
, то криволинейный интеграл вычисляется по формуле:
.gif) . Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле:
. Если плоская кривая задана в явном виде, то криволинейный интеграл вычисляется по формуле: .gif) .
.
38. Скалярное поле.
Скалярное поле. Если каждой точке ![]() пространства ставится в соответствие скалярная величина
пространства ставится в соответствие скалярная величина ![]() , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также
, то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также
![]() или
или ![]()
![]() . Поле может быть плоским, если
. Поле может быть плоским, если ![]() , центральным (сферическим), если
, центральным (сферическим), если ![]() , цилиндрическим, если
, цилиндрическим, если ![]() .
.
Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых ![]() принимает постоянное значение. Их уравнение:
принимает постоянное значение. Их уравнение: ![]() . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:
. В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение: ![]() . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.
. В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.
Производная по направлению и градиент скалярного поля. Пусть ![]() - единичный вектор с координатами
- единичный вектор с координатами ![]() ,
, ![]() - скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле
- скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле .gif) . Производная по направлению представляет собой скалярное произведение вектора
. Производная по направлению представляет собой скалярное произведение вектора ![]() и вектора с координатами
и вектора с координатами .gif) , который называется градиентом функции
, который называется градиентом функции ![]() и обозначается
и обозначается ![]() . Поскольку
. Поскольку .gif) , где
, где ![]() - угол между
- угол между ![]() и
и ![]() , то вектор
, то вектор ![]() указывает направление скорейшего возрастания поля
указывает направление скорейшего возрастания поля ![]() , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:
, а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:
![]()
![]()
![]()
![]()
.gif)
39. Векторное поле.
Векторное поле. Если каждой точке ![]() пространства ставится в соответствие вектор
пространства ставится в соответствие вектор ![]() , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде:
, то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде: ![]() . Скалярные функции
. Скалярные функции ![]() однозначно определяют векторное поле. Векторное поле может быть плоским, если
однозначно определяют векторное поле. Векторное поле может быть плоским, если ![]() , сферическим, когда
, сферическим, когда ![]() ,
, ![]() , цилиндрическим, когда
, цилиндрическим, когда ![]() ,
, ![]() .
.
Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор ![]() является касательным вектором. Через каждую точку
является касательным вектором. Через каждую точку ![]() проходит одна линия тока. За исключением точек, где поле не определено или
проходит одна линия тока. За исключением точек, где поле не определено или ![]() , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид:
, линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид: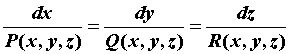
40. Поток векторного поля.
Поток векторного поля. Рассмотрим кусок поверхности ![]() , заданной уравнением
, заданной уравнением ![]() . Пусть выполняется условие
. Пусть выполняется условие ![]() , что означает, что в каждой точке поверхности существует нормаль с направляющим вектором
, что означает, что в каждой точке поверхности существует нормаль с направляющим вектором ![]() . Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля
. Выберем одну из сторон поверхности следующим образом: построим на поверхности достаточно малый замкнутый контур, на котором задано направление обхода. Построим вектор нормали в точке поверхности, лежащей внутри контура. Если из конца вектора нормали обход контура кажется происходящим против часовой стрелки, то будем называть сторону поверхности, обращенную к вектору нормали положительной стороной. Таким образом, будем рассматривать ориентированную двухстороннюю поверхность, а односторонние поверхности лист Мебиуса, бутылку Клейна оставим в покое. Потоком векторного поля ![]() через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода)
через ориентированную поверхность называется поверхностный интеграл по площади поверхности (1-го рода) ![]() , где -
, где - .gif) единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи.
единичный вектор нормали, направленный в положительную сторону. Выбор положительной стороны обычно диктуется физическими условиями задачи.
Непосредственное вычисление потока. Поскольку поток векторного поля определен с помощью поверхностного интеграла, вычисление потока сводится к вычислению такого интеграла от функции ![]() , где
, где ![]() - компоненты векторного поля,
- компоненты векторного поля, ![]() - направляющие косинусы вектора нормали.
- направляющие косинусы вектора нормали.
41. Формула Остроградского.
Поток векторного поля через замкнутую поверхность. Рассмотрим кусочно-гладкую двухстороннюю замкнутую ориентированную поверхность ![]() . Поток векторного поля
. Поток векторного поля ![]() через замкнутую поверхность
через замкнутую поверхность![]() является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости.
является важной характеристикой поля и позволяет судить о наличии источников и стоков поля. При непосредственном вычислении потока через замкнутую поверхность приходится разбивать ее на части, однозначно проектируемые на координатные плоскости.
Формула Остроградского. Пусть замкнутая поверхность ![]() ограничивает некоторый объем
ограничивает некоторый объем ![]() . Тогда в декартовых координатах справедлива формула Остроградского:
. Тогда в декартовых координатах справедлива формула Остроградского: .gif) , где
, где ![]() - компоненты векторного поля.
- компоненты векторного поля.
Дивергенция векторного поля. Дивергенцией ![]() векторного поля
векторного поля ![]() называется
называется .gif) . Точка
. Точка ![]() находится внутри замкнутой поверхности
находится внутри замкнутой поверхности ![]() , ограничивающей объем
, ограничивающей объем ![]() , который при вычислении предела стягивается в эту точку.
, который при вычислении предела стягивается в эту точку. ![]() является скалярной величиной и служит мерой источников поля. Если в некоторой области поля
является скалярной величиной и служит мерой источников поля. Если в некоторой области поля ![]() , то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах:
, то источников поля в этой области нет. Такое поле называют соленоидальным. Используя формулу Остроградского, нетрудно получить выражение для вычисления дивергенции в декартовых координатах: .gif) . Из свойств частных производных следуют свойства дивергенции векторного поля:
. Из свойств частных производных следуют свойства дивергенции векторного поля:
![]()
![]()
![]()
![]()
42. Криволинейный интеграл в векторном поле.
Криволинейный интеграл в векторном поле. Пусть заданы некоторое векторное поле ![]() и кривая АВ (А - начальная точка, В - конечная). Криволинейный интеграл в векторном поле
и кривая АВ (А - начальная точка, В - конечная). Криволинейный интеграл в векторном поле ![]() есть скаляр, полученный следующим образом:
есть скаляр, полученный следующим образом:
Разобьем кривую точками А=А0, А1, А2-Аn=В на n частей, приближенно изображаемых векторами![]() (разбиение
(разбиение ![]() ).
).
Обозначим ![]() .
.
На границе или внутри каждой элементарной дуги Аi-1Ai выберем точку, которой соответствует радиус-вектор ![]() и составим интегральную сумму
и составим интегральную сумму .gif) .
.
Если существует ![]() и он не зависит от разбиения
и он не зависит от разбиения ![]() и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:
и выбора точек, то этот предел называется криволинейным интегралом в векторном поле. В декартовой системе координат:![]() , где
, где ![]() - компоненты векторного поля.
- компоненты векторного поля.
Если кривая задана в параметрической форме:
![]() , то вычисление криволинейного интеграла сводится к определенному интегралу:
, то вычисление криволинейного интеграла сводится к определенному интегралу:
.gif) . Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла:
. Используя определение и формулу для вычисления нетрудно получить свойства криволинейного интеграла:
![]()
![]()
![]()
![]()
Подчеркнем, что, в отличие от криволинейного интеграла по длине дуги, криволинейный интеграл в векторном поле меняет знак при изменении направления интегрирования.
Если ![]() векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает
векторное поле, описывающее физическое силовое поле, то криволинейный интеграл выражает работу, которую совершает ![]() сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ.
сила при переносе материальной точки из пункта А в пункт В вдоль кривой АВ.
Циркуляция векторного поля. Важной характеристикой векторного поля является циркуляция векторного поля, которая равна криволинейному интегралу по замкнутой кривой в области поля, или, как говорят, по замкнутому контуру: ![]() . Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.
. Циркуляция векторного поля является скалярной величиной и характеризует вихревые свойства поля. Если в некоторой области поля циркуляция равна нулю, то поле называют безвихревым.
43. Формула Стокса.
Формула Стокса. Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности ![]() , край которой образуется кусочно-гладкой кривой
, край которой образуется кусочно-гладкой кривой ![]() . Выберем положительную сторону поверхности (из конца единичного вектора нормали
. Выберем положительную сторону поверхности (из конца единичного вектора нормали ![]() обход границы представляется против часовой стрелки). Для циркуляции векторного поля
обход границы представляется против часовой стрелки). Для циркуляции векторного поля ![]() вдоль контура границы имеет место формула Стокса:
вдоль контура границы имеет место формула Стокса: .gif) , где
, где ![]() - компоненты векторного поля,
- компоненты векторного поля, ![]() - направляющие косинусы вектора нормали.
- направляющие косинусы вектора нормали.
Ротор векторного поля. Рассмотрим в пространстве замкнутый контур ![]() с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали
с выбранным направлением обхода, лежащий в ориентированной плоскости на ее положительной стороне (из конца единичного вектора нормали ![]() обход контура представляется против часовой стрелки). Ротором
обход контура представляется против часовой стрелки). Ротором ![]() (или вихрем) векторного поля в точке
(или вихрем) векторного поля в точке ![]() называется вектор, проекция которого на направление вектора нормали есть
называется вектор, проекция которого на направление вектора нормали есть .gif) . Точка лежит
. Точка лежит ![]() на плоскости внутри контура
на плоскости внутри контура ![]() , который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором
, который стягивается в эту точку при вычислении предела. Поскольку ротор поля определяется через циркуляцию, то он тоже является мерой завихренности поля. Найдем компоненты ротора в декартовой системе координат, воспользовавшись формулой Стокса. Для этого выберем сначала координатную плоскость y0z с нормальным вектором ![]() , затем x0z,
, затем x0z, ![]() , затем x0y,
, затем x0y, ![]() . Применяя каждый раз теорему о среднем для интеграла, получим:
. Применяя каждый раз теорему о среднем для интеграла, получим: .gif)
Теперь теорема Стокса может быть сформулирована следующим образом: циркуляция векторного поля вдоль контура равна потоку ротора поля через поверхность, натянутую на этот контур. Выражение для ротора поля проще запомнить, если записать его в виде определителя:.gif) . Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:
. Используя свойства частных производных и определителей, получим следующие свойства ротора векторного поля:
![]()
![]()
![]()
![]()
44. Потенциальное поле.
Потенциальное поле. Если векторное поле ![]() , то оно называется потенциальным, а скалярное поле
, то оно называется потенциальным, а скалярное поле ![]() , соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого
, соответственно, его потенциалом. Самым известным примером такого соответствия является электрическое поле, напряженность которого ![]() , где
, где ![]() - потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически.
- потенциал электрического поля. Минус в формуле связан с историческим выбором направления вектора напряженности от плюса к минусу, когда уже умели тереть шерсть об янтарь, но не знали, как это описывать математически.
Условие потенциальности поля. Пусть задано скалярное поле ![]() , причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим
, причем данная функция дважды непрерывно дифференцируема. Напомним, что в этом случае смешанные частные производные второго порядка не зависят от порядка дифференцирования. Вычислим .gif) .
.
Нетрудно видеть, что при этих условиях получается тождественный ноль. То есть, если поле потенциальное, то его ![]() .
.
Вычисление потенциала векторного поля. Если мы убедились, что поле ![]() является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле:
является потенциальным, то есть его ротор равен нулю, то представляет интерес вычислить потенциал этого поля. Для этого рассмотрим криволинейный интеграл в данном векторном поле: ![]() , где точки А и В - начальная и конечная точки кривой. Поскольку
, где точки А и В - начальная и конечная точки кривой. Поскольку .gif) , то скалярное произведение векторов
, то скалярное произведение векторов ![]() и
и ![]() является полным дифференциалом функции
является полным дифференциалом функции ![]() :
: .gif) . Поэтому из свойств криволинейного интеграла следует, что
. Поэтому из свойств криволинейного интеграла следует, что ![]() . Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это - бесконечно удаленная точка). Тогда
. Смысл полученной формулы состоит в том, что работа поля по перемещению материальной точки из А в В не зависит от пути интегрирования, а только от конечной и начальной точек, точнее, от разности потенциалов в этих точках. Понятие разности потенциалов хорошо известно из физики. Для вычисления потенциала поля в произвольной точке В выберем начальную точку А, от которой начнем отсчет (в физике часто это - бесконечно удаленная точка). Тогда ![]() . Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая
. Поскольку интеграл не зависит от пути интегрирования, то выберем его так, как нам удобно: сначала параллельно оси 0х, потом параллельно 0у, наконец, параллельно 0z. Обозначая ![]() , получим:
, получим:
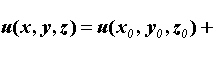
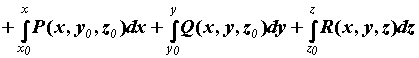 .
.
Здесь ![]() - компоненты векторного поля
- компоненты векторного поля ![]() . Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.
. Поскольку выбор начальной точки произволен, потенциал поля определяется с точностью до произвольной постоянной, которая определяется физическими соображениями.
Комментарии
Простите, не понял: сие есть стандартный курс
Курс по математическому анализу
или какое-то применение МАТЛАБа в курсе высшей математике?
В данном случае стандартный курс
Тогда зачем он здесь?
В то же время, применение МАТЛАБа в изложении высшей математики, ПРАВИЛЬНОЕ ПРИМЕНЕНИЕ -- в высшей мере актуально и нетривиально.