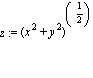Различные системы координат на плоскости и в пространстве

В декартовой системе координат поверхность задана уравнением 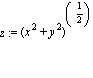. Перепишем это уравнение в сферической системе координат.

>

restart;

Уравнение поверхности.

>	z:=sqrt(x^2+y^2);

Нарисуем поверхность.

>	with(plots):

Warning, the name changecoords has been redefined

>	plot3d(z,x=-5..5,y=-5..5);

Сферические координаты связаны с декартовыми по формулам , .

>	x:=r*cos(phi)*sin(theta); y:=r*sin(phi)*sin(theta); z:=r*cos(theta) ;

Уравнение принимает следующий вид (применяем упрощение тригонометрических выражений):

>	z=simplify(sqrt(x^2+y^2),trig) assuming r>0;

Выражаем из предыдущего уравнения .

>	theta:=solve(%,theta);

Получили уравнение поверхности в сферических координатах.