Пример 3. Определение кратности корня методом Ньютона
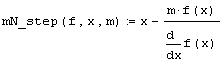

![]()
![]()
![]()
Пример 3. Определение кратности корня методом Ньютона |
|
| Метод Ньютона | 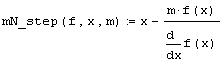 |
|
|
| Рассмотрим уравнение: |
|
| Корни уравнения: |
|
| Кратность корней - 2 | |
| Значение первого корня | |
| Найдем кратность корней эмпирически: | |
|
|
|
|
| Минимальное значение числа итераций - 7 при m=2, следовательно кратность корней 2. | |
| Заметим, что функция root дает только 7 верных цифр: | |
|
|