Пример 5. Приведение уравнения к виду, удобному для итераций
Найдем корень с помощью встроенной функции root:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 5. Приведение уравнения к виду, удобному для итераций |
|||
 |
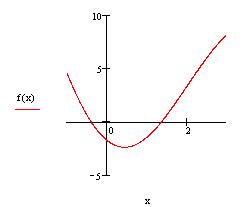
Будем искать простой корень уравнения ,
находящийся на отрезке локализации [-0.4,0] Найдем корень с помощью встроенной функции root: |
||
| 1 способ.
Приведем уравнение к виду x=f(x) , где |
|||
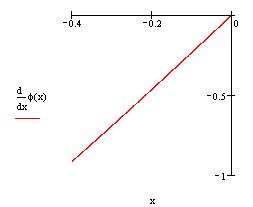
| Проверим условие сходимости: |
|||
| График производной | |||
 |
Макимальное по модулю значение
производной итерационной функции достигается в
левом конце отрезка |
||
|
|||
| Выполним 3 итерации по расчетной формуле x= f(x) | |||
| 1 итерация | |||
| 2 итерация | |||
| 3 итерация | |||
| Погрешность найденного значения: |
|
||
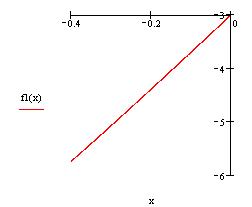
| 2 способ. Приведем уравнение к виду x=x-af(x) , где итерационная функция f(x)=x-af(x), a-итерационный параметр. | |||
| График производной f1(x) | Макимальное и минимальное значения производной достигаются на концах отрезка | ||
 |
|
|
|
| Выполним 3 итерации по расчетной формуле x= f(x)=x - af(x)) | |||
| 1 итерация | |||
| 2 итерация | |||
| 3 итерация | |||
| Погрешность найденного значения: |
|
||