случайная величина ~ функция
распределения ~ распределение
дискретной случайной величины
Случайной величиной называется
числовая функция от случайных событий.
Например, случайной величиной является число
очков, выпавших при бросании игральной кости, или
рост случайно выбранного из учебной группы
студента.
В первом случае мы имеем дело с дискретной
случайной величиной (она принимает значения из
дискретного числового множества 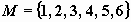 ; во втором
случае - с непрерывной случайной величиной
(она принимает значения из непрерывного
числового множества - из промежутка числовой
прямой ; во втором
случае - с непрерывной случайной величиной
(она принимает значения из непрерывного
числового множества - из промежутка числовой
прямой 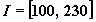 . .
Каждая случайная величина полностью
определяется своей функцией распределения. В
дальнейшем случайные величины будем обозначать
греческими буквами.
Если 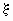 - случайная
величина, то функция - случайная
величина, то функция
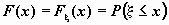
называется функцией распределения случайной
величины 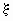 . Здесь . Здесь 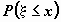 - вероятность того, что
случайная величина - вероятность того, что
случайная величина 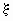 принимает
значения, не превосходящие числа принимает
значения, не превосходящие числа 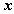 . .
Функция распределения любой случайной
величины обладает следующими свойствами:
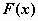 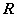 ; ;
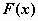 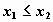 , то , то 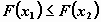 ; ;
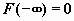 , , 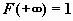 , , 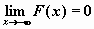 и и 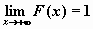 ; ;
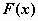 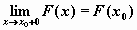 . .
Функция распределения содержит всю информацию
об этой случайной величине и поэтому изучение
случайной величины заключается в исследовании
ее функции распределения, которую часто
называют просто распределением. Так что,
когда говорят о нормальном распределении, то
подразумевают случайную величину, имеющую
нормальную функцию распределения.
У дискретной случайной величины функция
распределения ступенчатая.
ПРИМЕР 1. Случайная величина
принимает значение числа очков, выпавшее при
однократном бросании кости. Определим ее функцию
распределения и построим ее график.
Если 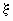 - дискретная
случайная величина, принимающая значения - дискретная
случайная величина, принимающая значения  с вероятностями с вероятностями  то таблица вида то таблица вида
называется распределением дискретной
случайной величины.
Вероятность того, что значение случайной
величины 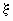 попадает в
интервал попадает в
интервал 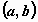 вычисляется
для дискретной случайной величины по формуле: вычисляется
для дискретной случайной величины по формуле:
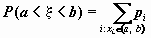 . .
ПРИМЕР 2. Вычислим вероятность
того, что при однократном бросании кости выпадет
число очков, которое меньше 5, но больше 2. |

