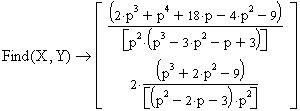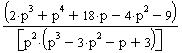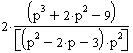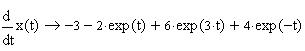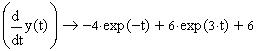Решение задачи Коши для уравнения операционным методом x' = x+2y-9t,   y' = 2x+y+4exp (t),   x (0) = 1,   y (0) = 2
	1.  Найдем изображения для -9t и 4exp (t)

	Для того, чтобы вычислить изображение, щелкните в панели Symbolic по ключевому слову laplace, удалите слева от ключевого слова одну метку, введите выражение для функции-оригинала, после ключевого слова введите запятую, затем имя переменной и щелкните вне рамки

	2.  Запишем систему для изображений:
	обозначим X - изображение x (t), Y - изображение для y (t), тогда изображение x' (t) равно pX-1, изображение y' (t) равно pY-2 и, следовательно, pX-1 = X+2Y-9/p^2,   pY-2 = 2X+Y+4/(p-1)

	3.  Определим и решим систему X (p), Y (p)

	Введите ключевое словпр Given, затем введите правую часть уравнения, знак символьного равенства (<Ctrl>+<=>), правую часть уравнения, функцию Find аргументов X, Y и щелкните вне выделяющей рамки

	4.  Выполним обратное преобразование Лапласа - найдем решение задачи Коши

	Для того, чтобы выполнить обратное преобразование Лапласа, выделите в найденном изображении переменную s, в меню Symbolics выберите раздел Transform и выполните (щелкнув по строке) операцию Inverse Laplace

	5.  Определим решение как функции переменного t

	6.  Подставим найденное решение в обе части уравнений системы и сравним полученные выражения и исходную систему

	7.  Проверим начальное условие