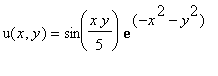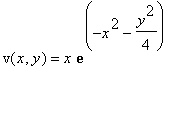Скалярное поле

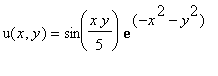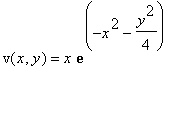Исследуем с помощью линий уровня поля u(x,y) = sin(1/5*x*y)*exp(-x^2-y^2) , v(x,y) = x*exp(-x^2-1/4*y^2) .

>    restart;

>    with(plots): 

Warning, the name changecoords has been redefined

Зададим уравнение первого поля.

>    u:=(x,y)->sin(x*y/5)*exp(-x^2-y^2);

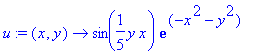
u := proc (x, y) options operator, arrow; sin(1/5*y*x)*exp(-x^2-y^2) end proc

Нарисуем поверхность, соответствующую данному уравнению.

>    plot3d(u(x,y),x=-2..2,y=-2..2, axes=frame);

[Maple Plot]

Нарисуем линии уровня, задающиеся уравнениями u(x,y) = const , с помощью функции implicitplot. Заметим, что скалярное поле принимает значения в интервале (-0.04, 0.04) . Разделим этот интервал на n  равных частей и нарисуем линии уровней границ полученных интервалов.

>    r:=0.04: n:=20:

>    display(seq(implicitplot(u(x,y)=r-2*(i-1)*r/n,
        x=-2..2,y=-2..2,style=line,axes=normal, color=COLOR(RGB,(r-(i-1)*r/n)/r,0,0)), i=1..n), insequence=false);

[Maple Plot]

Для изображения линий уровня удобно использовать функцию contourplot пакета plots.

>    contourplot(u(x,y),x=-3..3,y=-3..3,contours=40);

[Maple Plot]

Сделаем то же самое для второго поля.

>    v:=(x,y)->x*exp(-x^2-y^2/4);

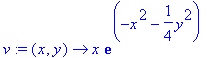
v := proc (x, y) options operator, arrow; x*exp(-x^2-1/4*y^2) end proc

Нарисуем поверхность, соответствующую уравнению поля.

>    plot3d(v(x,y),x=-3..3,y=-5..5, axes=frame);

[Maple Plot]

Здесь скалярное поле принимает значения в интервале (-0.45, 0.45) .

>    r:=0.45: n:=40:

>    display(seq(implicitplot(v(x,y)=r-2*(i-1)*r/n,
        x=-3..3,y=-4..4,style=line,axes=normal, color=COLOR(RGB,(r-(i-1)*r/n)/r,0,0)), i=1..n), insequence=false);

[Maple Plot]

Нарисуем линии уровня с помощью команды contourplot.

>    contourplot(v(x,y),x=-3..3,y=-4..4,contours=40);

[Maple Plot]