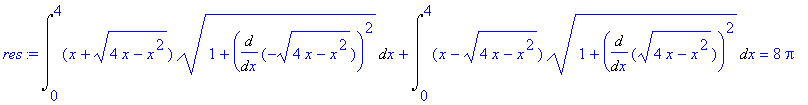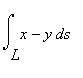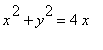Криволинейный интеграл по длине дуги

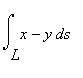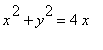Вычислим  Int(x-y,s = L .. ``), где L  - окружность x^2+y^2 = 4*x.

>   restart;

>   with(student):with(plots):

Warning, the name changecoords has been redefined

Зададим интегрируемую функцию.

>   f:=(x,y)->x-y;

f := proc (x, y) options operator, arrow; x-y end proc

Зададим кривую.

>   L:={x^2+y^2-4*x=0};

L := {x^2+y^2-4*x = 0}

Нарисуем заданную кривую.

>   implicitplot(L,x=0..4,y=-4..4);

[Maple Plot]

Вычислим интеграл, приведя функцию и кривую к параметрическому виду. Для этого сначала сдвинем систему координат так, чтобы центр заданной окружности совпадал с началом координат.

>   x:=u+2;y:=v;

x := u+2

y := v

В новых координатах функция и уравнение окружности примут вид:

>   f(x,y);simplify(L);

u+2-v

{u^2-4+v^2 = 0}

Перейдем к параметру t по следующим формулам:

>   u:=2*cos(t);v:=2*sin(t);

u := 2*cos(t)

v := 2*sin(t)

Вид функции и уравнения окружности:

>   f(x,y);simplify(L);

2*cos(t)+2-2*sin(t)

{0 = 0}

Последнее тождество означает, что u := 2*cos(t), v := 2*sin(t) и есть параметрическое задание нашей окружности. Параметр t пробегает интервал от 0 до 2*Pi.

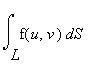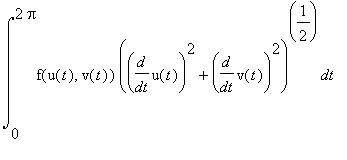Теперь интеграл можно рассчитать по следующей формуле: Int(f(u,v),S = L .. ``) = Int(f(u(t),v(t))*(diff(u(t),t)^2+diff(v(t),t)^2)^(1/2),t = 0 .. 2*Pi).

>   Int(f(x,y)*sqrt((Diff(u,t))^2+(Diff(v,t))^2),t=0..2*Pi)=int(f(x,y)*sqrt((diff(u,t))^2+(diff(v,t))^2),t=0..2*Pi);

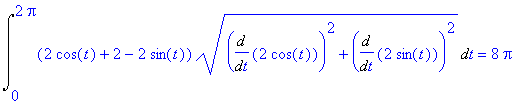
Int((2*cos(t)+2-2*sin(t))*(Diff(2*cos(t),t)^2+Diff(2*sin(t),t)^2)^(1/2),t = 0 .. 2*Pi) = 8*Pi

Для расчета интеграла по длине дуги можно использовать встроенную функцию LineInt.

>   restart;

>   with(student):

>   L:=Lineint(2*(cos(t)-sin(t)+1),u=2*cos(t),v=2*sin(t),t=0..2*Pi);

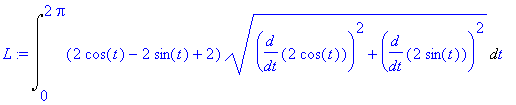
L := Int((2*cos(t)-2*sin(t)+2)*(diff(2*cos(t),t)^2+diff(2*sin(t),t)^2)^(1/2),t = 0 .. 2*Pi)

>   value(%);

8*Pi

Интеграл можно рассчитать, используя явное задание кривой. Окружность разложим на две части: дуги над и под осью x. Назовем соответствующие функции y1 и y2.

>   restart;

>   y1:=x->sqrt(4*x-x^2);

y1 := proc (x) options operator, arrow; sqrt(4*x-x^2) end proc

>   y2:=x->-sqrt(4*x-x^2);

y2 := proc (x) options operator, arrow; -sqrt(4*x-x^2) end proc

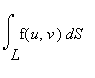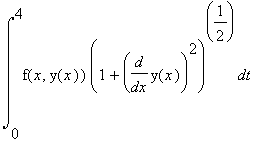
Для вычисления интеграла используем формулу Int(f(u,v),S = L .. ``) = Int(f(x,y(x))*(1+diff(y(x),x)^2)^(1/2),t = 0 .. 4)

Интеграл по верхней дуге.

>   Int((x-y1(x))*sqrt(1+(Diff(y1(x),x))^2),x=0..4)=int((x-y1(x))*sqrt(1+(diff(y1(x),x))^2),x=0..4);

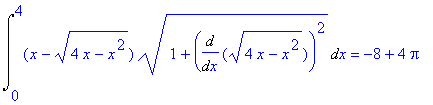
Int((x-(4*x-x^2)^(1/2))*(1+Diff((4*x-x^2)^(1/2),x)^2)^(1/2),x = 0 .. 4) = -8+4*Pi

Интеграл по нижней дуге.

>   Int((x-y2(x))*sqrt(1+(Diff(y2(x),x))^2),x=0..4)=int((x-y2(x))*sqrt(1+(diff(y2(x),x))^2),x=0..4);

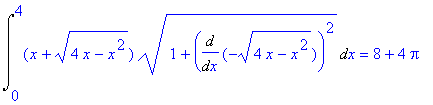
Int((x+(4*x-x^2)^(1/2))*(1+Diff(-(4*x-x^2)^(1/2),x)^2)^(1/2),x = 0 .. 4) = 8+4*Pi

Искомый интеграл - сумма двух найденных.

>   res:=%+%%;

res := Int((x+(4*x-x^2)^(1/2))*(1+Diff(-(4*x-x^2)^(1/2),x)^2)^(1/2),x = 0 .. 4)+Int((x-(4*x-x^2)^(1/2))*(1+Diff((4*x-x^2)^(1/2),x)^2)^(1/2),x = 0 .. 4) = 8*Pi