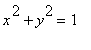Поверхностный интеграл по площади поверхности

Вычислим площадь куска поверхности , вырезанного цилиндром .

>

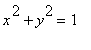restart;

Нарисуем заданную поверхность.

>	with(plots):

Warning, the name changecoords has been redefined

>	A:=plot3d(x*y,x=-1.5..1.5,y=-1.5..1.5):

>	B:=cylinderplot(1,theta=0..2*Pi,z=-1..1):

>	display([A,B],orientation=[15,37]);

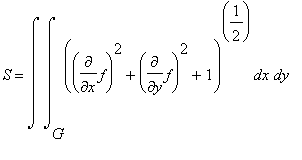Поверхность задана уравнением вида , поэтому ее площадь вычисляется по формуле . Здесь G  - проекция поверхности на плоскость x0y , в задаче это круг единичного радиуса с центром в начале координат.

>	with(student):

>	S:=Doubleint(sqrt(diff(f(x,y),x)^2+diff(f(x,y),y)^2+1),x,y,G);

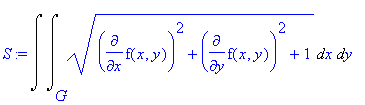
>	f(x,y):=x*y;

>

S;

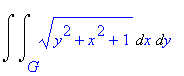
Перейдем к полярным координатам.

>	S:=changevar({x=r*cos(t),y=r*sin(t)}, S,[t,r] );

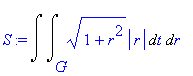
В полярных координатах интеграл сводится к повторному.

>	S:=Int(Int((1+r^2)^(1/2)*abs(r),r=0..1),t=0..2*Pi);

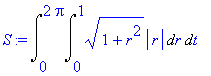
>	S:=int(int((1+r^2)^(1/2)*abs(r),r=0..1),t=0..2*Pi);

Поверхностные интегралы в Maple можно  вычислять с помощью функции SurfaceInt ( f, dom ) пакета VectorCalculus. Здесь f - интегрируемая функция, равная единице в случае вычисления площали поверхности, dom - поверхность.

>	with(VectorCalculus):

Warning, the assigned names <,> and <|> now have a global binding

Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series

>	S:=SurfaceInt( 1, [x,y,z] = Surface( <s,t,s*t>, [s,t] = Circle( <0,0>, 1 ) ) );