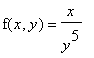 по области
по области
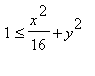 ,
,
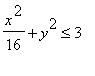 ,
,
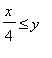 .
.
Замена переменных в кратных интегралах
Вычислим двойной интеграл от функции
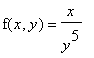 по области
по области
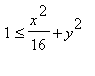 ,
,
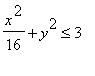 ,
,
![]() ,
,
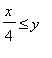 .
.
| > | restart; |
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | f:=(x,y)->x/y^5; |
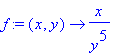
| > | S:={x^2/16+y^2-1>=0,x^2/16+y^2-3<=0,x>=0,y-x/4>=0}; |
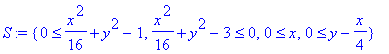
Нарисуем заданную область.
| > | implicitplot(S,x=0..7,y=0..2); |
![[Maple Plot]](images/ex38.gif)
Перейдем к обощенным полярным координатам.
| > | x:=4*r*cos(t);y:=r*sin(t); |
![]()
![]()
| > | simplify(S); |
![]()
| > | f(x,y); |
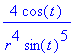
| > | S:=Int(Int(f(x,y)*4*r,r=1..sqrt(3)),t=Pi/4..Pi/2); |
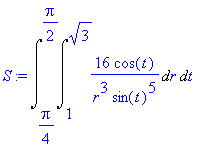
| > | S:=value(%); |
![]()