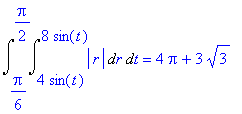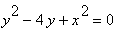 ,
,
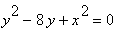 ,
,
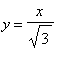 ,
,
Замена переменных в кратных интегралах
Вычислим якобианы для полярных и обобщенных полярных координат. Вычислим площадь фигуры, ограниченной линиями
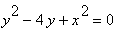 ,
,
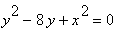 ,
,
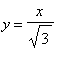 ,
,
![]() .
.
| > | restart; |
Полярные координаты.
| > | x:=r*cos(t);y:=r*sin(t); |
![]()
![]()
Вычислим якобиан.
| > | with(LinearAlgebra): |
| > | M:=Matrix([[diff(x,r),diff(x,t)],[diff(y,r),diff(y,t)]]); |
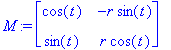
| > | J:=Determinant(M); |
![]()
| > | simplify(J,trig); |
![]()
Обобщенные полярные координаты.
| > | x:=a*r*cos(t);y:=b*r*sin(t); |
![]()
![]()
Вычислим якобиан.
| > | M:=Matrix([[diff(x,r),diff(x,t)],[diff(y,r),diff(y,t)]]); |
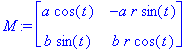
| > | J:=Determinant(M); |
![]()
| > | simplify(J,trig); |
![]()
Для вычисления якобианов можно использовать функцию Jacobian пакета VectorCalculus.
| > | with(VectorCalculus): |
Warning, the names CrossProduct and DotProduct have been rebound
Warning, the assigned names <,> and <|> now have a global binding
Warning, these protected names have been redefined and unprotected: *, +, ., Vector, diff, int, limit, series
Полярные координаты.
| > | (M,d):=Jacobian( [r*cos(t),r*sin(t)], [r,t], 'determinant' ); |
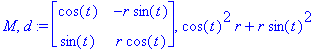
| > | simplify(d,trig); |
![]()
Обобщенные полярные координаты.
| > | (M,d):=Jacobian( [a*r*cos(t),b*r*sin(t)], [r,t], 'determinant' ); |
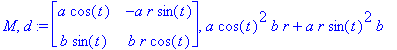
| > | simplify(d,trig); |
![]()
| > | restart; |
Нарисуем заданную фигуру.
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | S:={y^2-4*y+x^2>0,y^2-8*y+x^2<0,y-x/sqrt(3)>0,x>0}; |
![]()
| > | implicitplot(S,x=0..5,y=0..8); |
![[Maple Plot]](images/ex120.gif)
Перейдем к полярным координатам.
| > | x:=r*cos(t);y:=r*sin(t); |
![]()
![]()
| > | simplify(S); |
![]()
| > | with(student): |
| > | x:='x':y:='y':S:='S': |
При переходе к полярным координатам под знаком интеграла появляется соответствующий якобиан.
| > | Doubleint(1,x,y,S)=Doubleint(abs(r),r,t,S); |
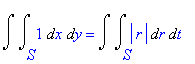
Перепишем двойной интеграл в виде повторного.
| > | Doubleint(abs(r),r,t,S)=Int(Int(abs(r),r=4*sin(t)..8*sin(t)),t=Pi/6..Pi/2); |
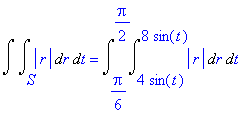
Вычислим интеграл с помощью функции int.
| > | Int(Int(abs(r),r=4*sin(t)..8*sin(t)),t=Pi/6..Pi/2)=int(int(abs(r),r=4*sin(t)..8*sin(t)),t=Pi/6..Pi/2); |