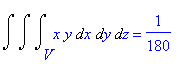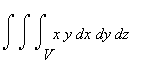 по области, ограниченной поверхностями
по области, ограниченной поверхностями
Двойной и тройной интегралы
Вычислим
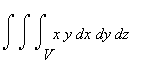 по области, ограниченной поверхностями
по области, ограниченной поверхностями
![]() ,
,
![]() .
.
> restart;
> with(plots):with(student):
Warning, the name changecoords has been redefined
Нарисуем область, по которой будем интегрировать.
> implicitplot3d({z=x*y,x+y=1,z=0},x=0..1,y=0..1,z=0..1);
![[Maple Plot]](images/ex54.gif)
Зададим интегрируемую функцию.
> f:=(x,y,z)->x*y;
![]()
Перепишем тройной интеграл в виде повторного. Сначала интегрируем по z в пределах от 0 до
xy
, а потом по области S в плоскости xy.
S = {
x + y
<1}.
> Tripleint(f(x,y,z),x,y,z,V)=Doubleint(Int(f(x,y,z),z=0..x*y),x,y,S);
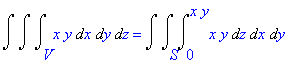
Двойной интеграл по области S сводится к повторному - сначала интегрируем по y от 0 до 1- x, а затем по x от 0 до 1.
> Tripleint(f(x,y,z),x,y,z,V)=Int(Int(Int(f(x,y,z),z=0..x*y),y=0..1-x),x=0..1);
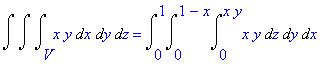
Вычислим интеграл, используя функцию int.
> Tripleint(f(x,y,z),x,y,z,V)=int(int(int(f(x,y,z),z=0..x*y),y=0..1-x),x=0..1);