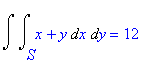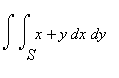Двойной и тройной интегралы

Вычислим 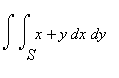по области, ограниченной прямыми .

> restart;

> with(plots):with(student):

Warning, the name changecoords has been redefined

Нарисуем область, по которой будем интегрировать. В случае, когда она задана линейными неравенствами, можно использовать функцию inequal.

> setoptions(axes=normal,scaling=constrained):

> inequal({x+y<6,y>x,y<2*x}, x=0..4, y=0..5, optionsfeasible=(color=green),optionsopen=(color=blue,thickness=2),optionsexcluded=(color=white) );

Найдем точки пересечения прямых.

> solve({x+y=6,y=2*x}); solve({x+y=6,y=x});

Нарисуем область, разделенную на две части прямой .

> implicitplot({y=x, x+y=6, y=2*x, x=2},x=0..3,y=0..4);

Зададим интегрируемую функцию.

> f:=(x,y)->x+y;

Перепишем двойной интеграл в виде повторного. Разложим интеграл в сумму интегралов по x от 0 до 2 и от 2 до 3. В этих пределах интегрируем сначала по y (в первом интеграле от x до 2x, во втором от x до 6-x), а затем по x.

> Doubleint(f(x,y),x,y,S)=Int(Int(f(x,y),y=x..2*x),x=0..2)+Int(Int(f(x,y),y=x..6-x),x=2..3);

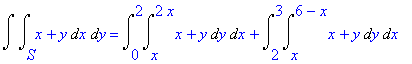
Вычислим интеграл, используя функцию int.

> Doubleint(f(x,y),x,y,S)=int(int(f(x,y),y=x..2*x),x=0..2)+int(int(f(x,y),y=x..6-x),x=2..3);