Нетрудно понять, что в исследуемой области находится максимум функции двух переменных, который можно найти обычным способом (см. занятие 31), следовательно, и условный максимум исследуемой функции u(x,y,z).

Для того, чтобы построить график функции двух переменных, выберите соответствующий сивол в панели  Graph, введите в помеченной позиции имя функции и щелкните вне пояя графика. Дважды щелкните по полю графика и установите в диалоговых окнах параметры изображения. Эти параметры можно менять не закрывая окно настройки, а только щелкая по кнопке Apply, чтобы посмотреть результат настройки. Перемещение указателя мыши по полю графика с нажатой левой кнопкой позволяет поворачивая график рассмотреть его со всех сторон. Мышь со скроллингом позволяет увеличить и уменьшить масштаб графика

Построим график этой функции

Ограничимся первым квадрантом, где x>0,y>0,z>0. Выразим, например, х через у и z и подставим в исследуемую функцию. При этом получим функцию двух переменных

и найдем ее экстремум при условии, что х и у лежат на плоскости

Теперь рассмотрим функцию трех переменных

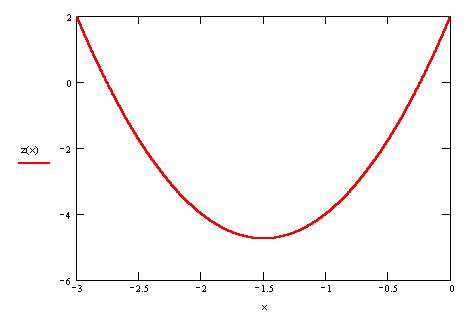
Таким образом, в точке х=-3/2 находится минимум функции z(x), а, следовательно, в точке (-3/2,-3/2) - условный минимум функции z(x,y).

Для того чтобы построить график, щелкните по символу декартова графика в панели Graph и введите в помеченных позициях возле координатных осей имена аргумента и функции.
Для того чтобы изобразить на одном графике несколько функций одного и того же аргумента, введите в позиции возле оси ординат имя первой функции, введите з а п я т у ю , имя следующей функции, запятую, и т.д., разделяя имена функций з а п я т о й.
Для того чтобы изменить стиль изображения, щелкните по графиуку дважды и измените параметры изображения в открывшемся временном окне настройки изображения.

Полученная функция одной переменной исследуется обычным способом. Чтобы не утомлять читателя, просто построим график этой функции, где все видно.

Выделите выражение в правой части и щелкните Simplify в меню Symbolics

Для этого выразим, например, у через х, и подставим в исследуемую функцию.

и найдем ее экстремум при условии, что х и у лежат на прямой

Рассмотрим функцию