Рассмотрим функцию
Функция положительна везде, кроме точки (1, 0), где она обращается в ноль, то есть имеем неравенство
По определению это и означает, что в точке (1, 0)
находится строгий локальный минимум.
Построим график функции
Для того, чтобы построить график функции двух
переменных, выберите соответствующий сивол в
панели
Graph, введите в помеченной позиции имя функции и
щелкните вне пояя графика. Дважды щелкните по
полю графика и установите в диалоговых окнах
параметры изображения. Эти параметры можно
менять не закрывая окно настройки, а только
щелкая по кнопке Apply, чтобы посмотреть результат
настройки. Перемещение указателя мыши по полю
графика с нажатой левой кнопкой позволяет
поворачивая график рассмотреть его со всех
сторон. Мышь со скроллингом позволяет увеличить
и уменьшить масштаб графика
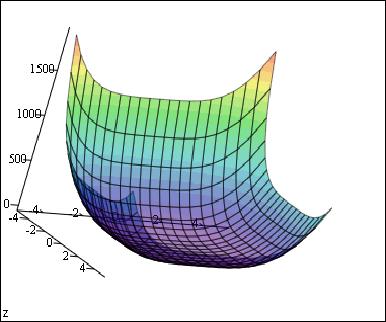
Рассмотрим теперь функцию
Поскольку здесь не очевидно, в какой точке
может иметь экстремум данная функция, найдем ее
стационарные точки, то есть точки, где частные
производные обращаются в ноль. Только в таких
точках может быть экстремум функции (необходимое
условие экстремума).
Вычислим частные производные.
Для
вычисления частной производной щелкните символ
дифференцирования в панели Calculus, введите
переменную дифференцирования, символ функции
или ее выражение, щелкните по стрелке в панели
Evaluation, затем вне выделяющей рамки.
Теперь ясно, что нас может интересовать точка (1,-1). В этой точке функция обращается в ноль. Однако, в отличие от предыдущего примера, в любой окрестности этой точки функция g(x,y) может быть как положительной, так и отрицательной, как каждый из сомножителей. Построим график функции
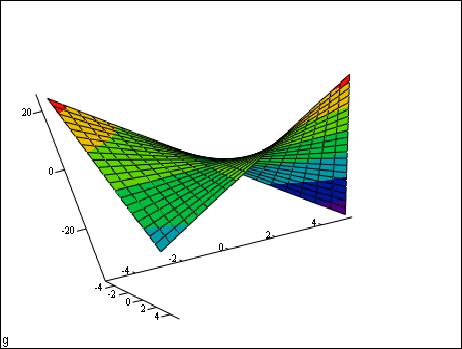
Теперь понятно. что исследуемая точка является седловой и в ней нет экстремума.